题目描述
对称就是最大的美学,现有一道关于对称字符串的美学。已知:
- 第1个字符串:R
- 第2个字符串:BR
- 第3个字符串:RBBR
- 第4个字符串:BRRBRBBR
- 第5个字符串:RBBRBRRBBRRBRBBR
相信你已经发现规律了,没错!就是第 i 个字符串 = 第 i – 1 号字符串取反 + 第 i – 1 号字符串;
取反(R->B, B->R);
现在告诉你n和k,让你求得第n个字符串的第k个字符是多少。(k的编号从0开始)
输入描述
第一行输入一个T,表示有T组用例;
解析来输入T行,每行输入两个数字,表示n,k
- 1 ≤ T ≤ 100;
- 1 ≤ n ≤ 64;
- 0 ≤ k < 2^(n-1);
输出描述
输出T行表示答案;
输出 "blue" 表示字符是B;
输出 "red" 表示字符是R。
备注:输出字符串区分大小写,请注意输出小写字符串,不带双引号。
用例
| 输入 | 5 1 0 2 1 3 2 4 6 5 8 |
| 输出 | redredblueblueblue |
| 说明 | 第 1 个字符串:R -> 第 0 个字符为R 第 2 个字符串:BR -> 第 1 个字符为R 第 3 个字符串:RBBR -> 第 2 个字符为B 第 4 个字符串:BRRBRBBR -> 第 6 个字符为B 第 5 个字符串:RBBRBRRBBRRBRBBR -> 第 8 个字符为B |
| 输入 | 1 64 73709551616 |
| 输出 | red |
| 说明 | 无 |
题目解析

上图所示,是第1~6个字符串,可以发现第6个已经很长了,那么本题的最多要求到第64个字符串,那么有多长呢?答:2^63,即 2^(n-1)。这个长度如果用字符串来存储的话,肯定爆内存,因此任何需要缓存字符串的动作都是禁止的。
我们只能找规律,来通过规律推导出第n个字符串的第k个字符。
那么规律是啥呢?

如上图黄框所示,我们可以发现,
第6个字符串的后半部分,和第5个字符串完全相同;
同理,
第5个字符串的后半部分,和第4个字符串完全相同;
第4个字符串的后半部分,和第3个字符串完全相同;
第3个字符串的后半部分,和第2个字符串完全相同;
第2个字符串的后半部分,和第1个字符串完全相同;
因此,如果我们要找到的k位于第n个字符串的后半部分,假设为get(n, k),那么其等价于 get(n-1, k – 2^(n-2)),按此逻辑递归,就可以一直找到第2个字符串或第1个字符串,而这两个字符串很好确认,分别是”R“,”BR“。
那么如果我们要找到第k个字符串,位于第n个字符串的前半部分呢?

可以发现,其实get(n,k),如果k <= 2^(n-2) ,则相当于 get(n-1, k) 的颜色取反。
本题的精度问题
根据一位考友反馈的100%Java代码来看,逻辑和本题一模一样,唯一的区别在于:
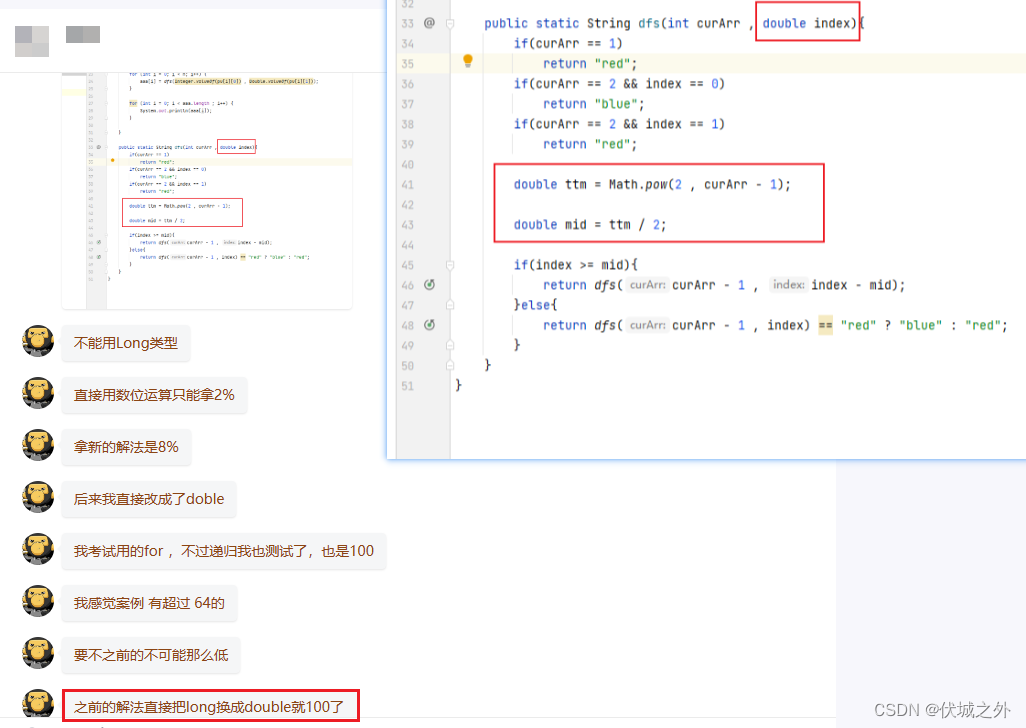
这个考友分析是可能存在超过64长度的字符串,因此需要使用更大范围的double类型。
但是之后又有一个Python语言的考友反馈,这种解法无法拿到100%,还是8%。这里给大家解释一下,Python天生支持大数(只要不进行除法,非整除),因此对于Python老解法,我未作任何改动,如下图所示
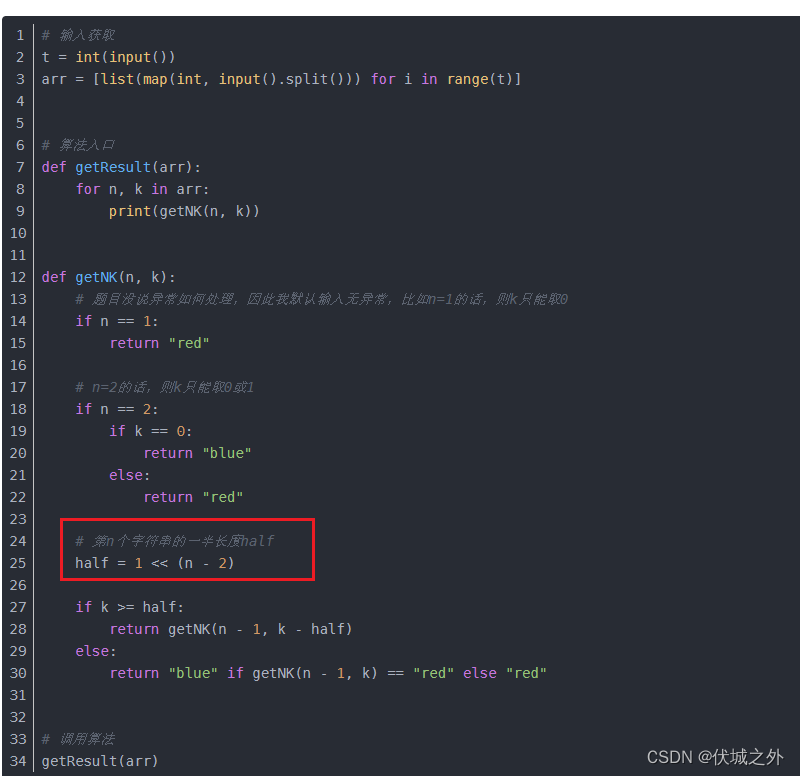
但是最后通过率只有8%。
不应该呀。为什么呢?
左思右想,发现,是对half的取值逻辑存在差异。
Java的是基于Math.pow(2, n-2)取得half,而Python是1 << n-2取得的half值,这两者有区别吗?
在逻辑上是没有区别的,但是实际上,当结果超过一定范围后,Math.pow会做四舍五入,即丢失精度。
Java如下图所示,2^58开始丢失精度,即Math.pow做了四舍五入
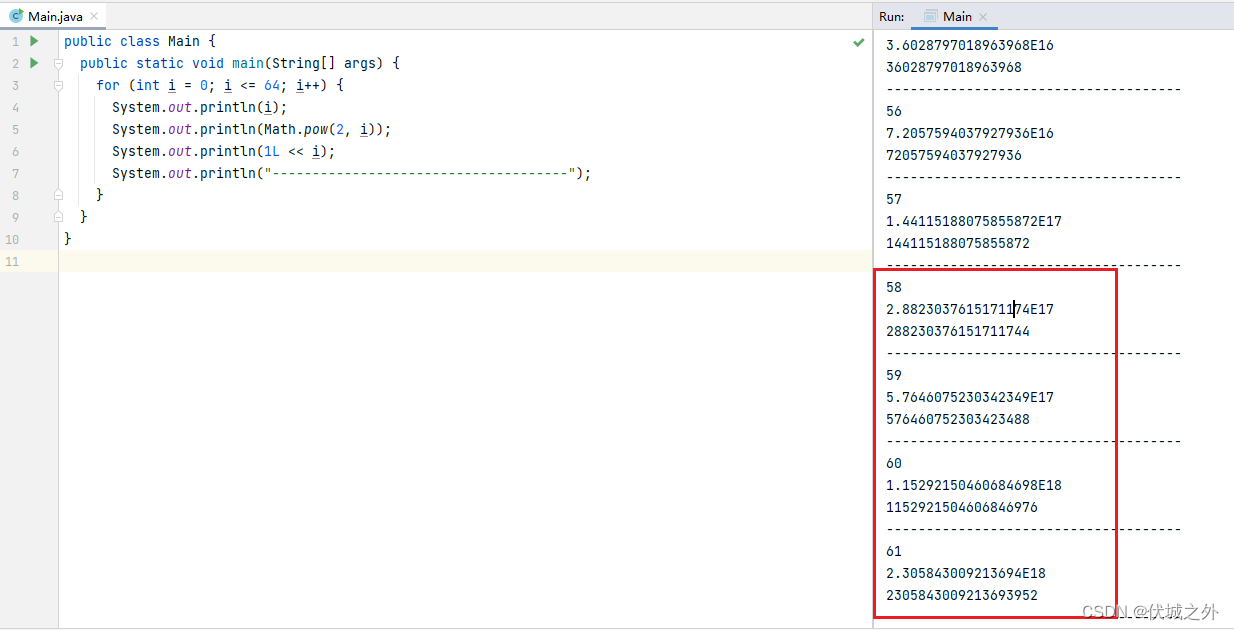
Python如下图所示,从2^55开始丢失精度,即Math.pow做了四舍五入
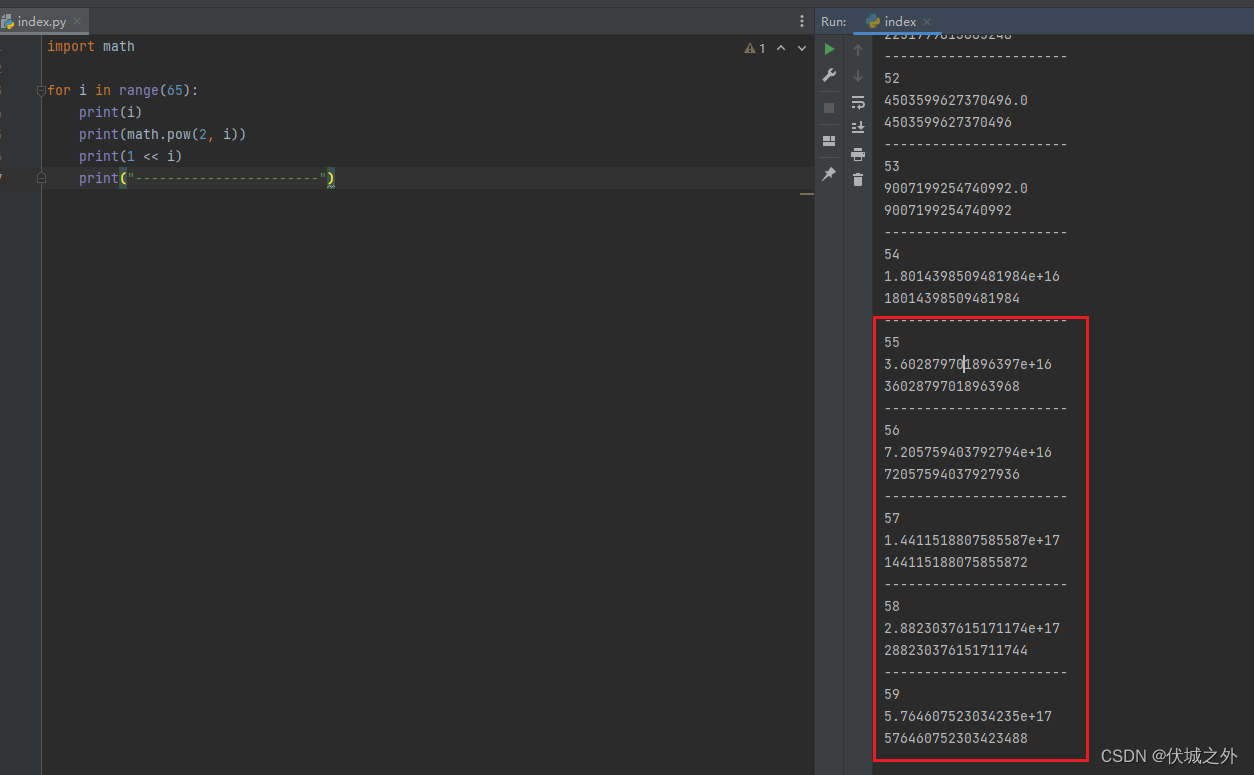
JS如下图所示,从2^55开始丢失精度,即Math.pow做了四舍五入
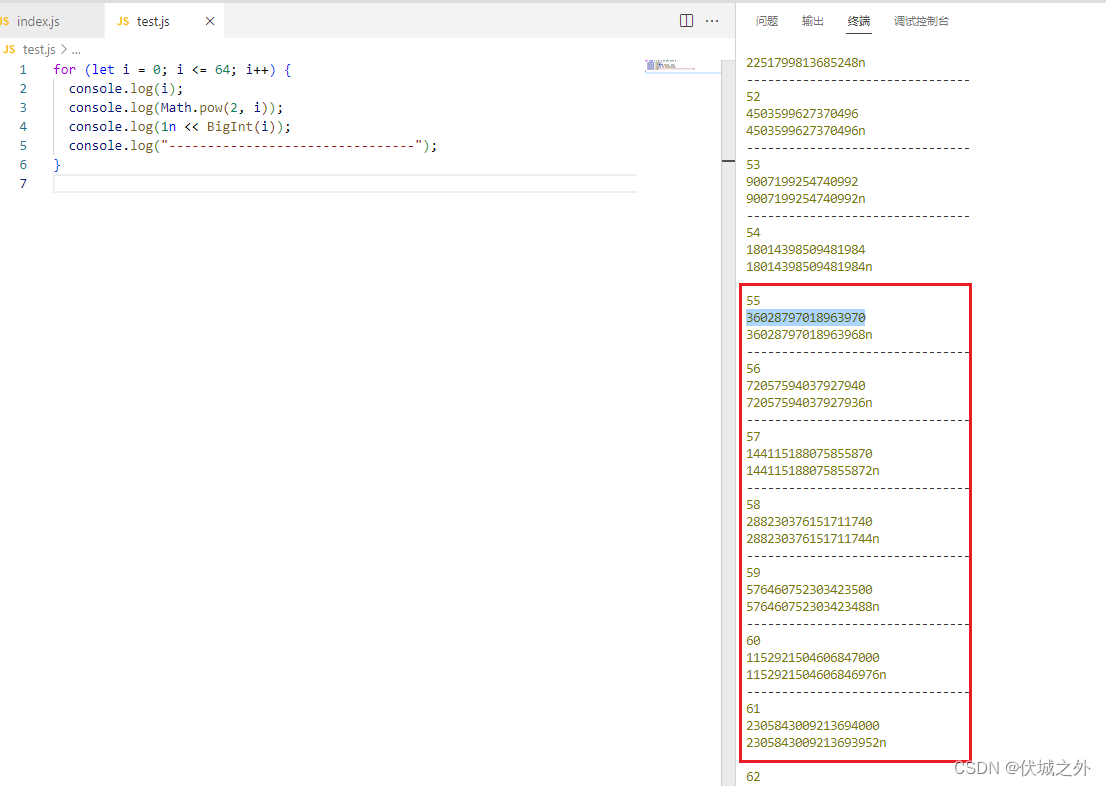
因此Math.pow和<<并不是等价的。
而本题需要使用Math.pow取half才能拿到满分。
但是,本题其实使用<<得到的答案才更加准确。
当然,到这里,本题的问题并没有解决,如下图所示



该场景是想求解第64个字符串的第4611686018427387905个字符的颜色。
即k = 4611686018427387905,half = math.pow(2, 62)
可以发现,不同的语言,这里产生的结果不同。其中JS返回的是1,而Java和Python返回的是0。
为啥呢?
Java



JS
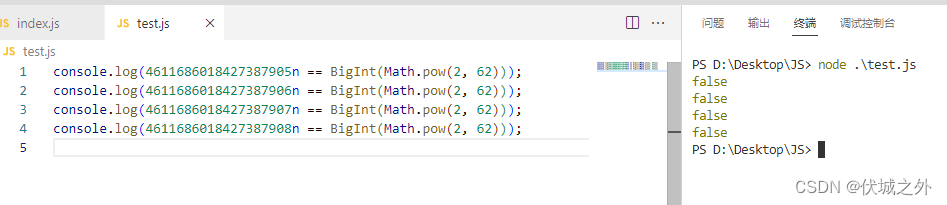

Python
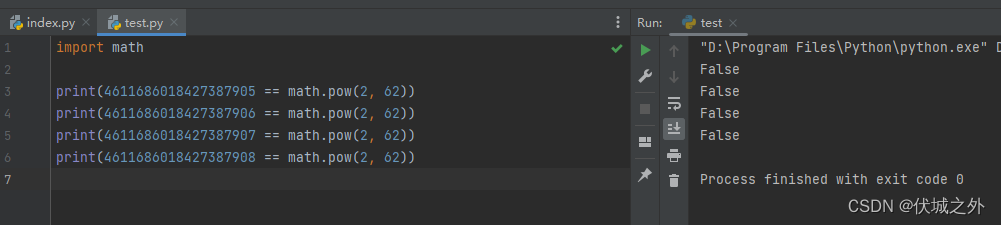



因此,其实我们要对输入的k值,转成双精度浮点型,来满足和math.pow的结果匹配。
这里Java和Python都是OK的。但是JS就苦逼了。因为JS没有大数+浮点的类型。
因此,本题Java和Python的代码可以妥协来适配满分。但是JS无法适配。
建议使用JS的同学遇到这题,可以采用偷分策略,即不需要任何算法,直接输入red或者blue,选择分值更高。
JavaScript算法源码
需要注意的是,本题中
- 1 ≤ n ≤ 64;
- 0 ≤ k < 2^(n-1);
也就说 k 最大值可以取到 2^63 – 1,即9223372036854775807,而这个数已经超过了JS的number类型的安全数范围,即-2^53 + 1 ~ 2^53 – 1,超范围的数会得到不准确的值,比如
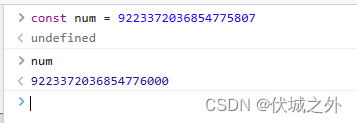
此时,我们应该考虑是BigInt代替Number类型来处理大数,而由于BigInt大数只能和BigInt大数进行运算,因此需要将程序中所有的数值全部变为BigInt类型。对于字面量数值,需要在字面量后面加个n,比如1是Number类型,那么1n就是BigInt类型的数值1。
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let t;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
t = lines[0] - 0;
}
if (t && lines.length === t + 1) {
lines.shift();
const arr = lines.map((line) => line.split(" ").map(BigInt));
getResult(arr);
lines.length = 0;
}
});
function getResult(arr) {
for (let [n, k] of arr) {
console.log(getNK(n, k));
}
}
function getNK(n, k) {
// 题目没说异常如何处理,因此我默认输入无异常,比如n=1的话,则k只能取0
if (n === 1n) {
return "red";
}
// n=2的话,则k只能取0或1
if (n === 2n) {
if (k === 0n) return "blue";
else return "red";
}
// 第n个字符串的一半长度half
let half = 1n << (n - 2n);
if (k >= half) {
return getNK(n - 1n, k - half);
} else {
return getNK(n - 1n, k) === "red" ? "blue" : "red";
}
}Java算法源码
需要注意的是,本题中
- 1 ≤ n ≤ 64;
- 0 ≤ k < 2^(n-1);
也就说 k 最大值可以取到 2^63 – 1,即9223372036854775807,而这个数刚好是Java的long类型最大值,因此不会造成整型溢出。但是我们代码中所有的数都必须使用long类型装载。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
double[][] arr = new double[t][2];
for (int i = 0; i < t; i++) {
arr[i][0] = sc.nextDouble();
arr[i][1] = sc.nextDouble();
}
getResult(arr);
}
public static void getResult(double[][] arr) {
for (double[] nk : arr) {
System.out.println(getNK(nk[0], nk[1]));
}
}
public static String getNK(double n, double k) {
if (n == 1) {
return "red";
}
if (n == 2) {
if (k == 0) return "blue";
else return "red";
}
double half = Math.pow(2, n - 2);
if (k >= half) {
return getNK(n - 1, k - half);
} else {
return "red".equals(getNK(n - 1, k)) ? "blue" : "red";
}
}
}
Python算法源码
需要注意的是,本题中
- 1 ≤ n ≤ 64;
- 0 ≤ k < 2^(n-1);
也就说 k 最大值可以取到 2^63 – 1,即9223372036854775807
关于Python处理大数的说明
即Python3支持任意大的整数运算。
因为本题中不涉及除法,因此无需额外处理。
# 输入获取
import math
t = int(input())
# 注意这里需要转float
arr = [list(map(float, input().split())) for i in range(t)]
# 算法入口
def getResult(arr):
for n, k in arr:
print(getNK(n, k))
def getNK(n, k):
# 题目没说异常如何处理,因此我默认输入无异常,比如n=1的话,则k只能取0
if n == 1:
return "red"
# n=2的话,则k只能取0或1
if n == 2:
if k == 0:
return "blue"
else:
return "red"
# 第n个字符串的一半长度half
half = math.pow(2, n - 2)
if k >= half:
return getNK(n - 1, k - half)
else:
return "blue" if getNK(n - 1, k) == "red" else "red"
# 调用算法
getResult(arr)
免责声明:
评论0