题目描述
现在有n个容器服务,服务的启动可能有一定的依赖性(有些服务启动没有依赖),其次服务自身启动加载会消耗一些时间。
给你一个 n x n 的二维矩阵useTime,其中
- useTime[i][i]=10 表示服务i自身启动加载需要消耗10s
- useTime[i][j] = 1 表示服务i启动依赖服务j启动完成
- useTime[i][k]=0 表示服务i启动不依赖服务k
其实 0<= i,j,k < n。
服务之间启动没有循环依赖(不会出现环),若想对任意一个服务i进行集成测试(服务i自身也需要加载),求最少需要等待多少时间。
输入描述
第一行输入服务总量 n,
之后的 n 行表示服务启动的依赖关系以及自身启动加载耗时
最后输入 k 表示计算需要等待多少时间后可以对服务 k 进行集成测试
其中 1 <= k <=n,1<=n<=100
输出描述
最少需要等待多少时间(s)后可以对服务 k 进行集成测试
用例
| 输入 | 3 5 0 0 1 5 0 0 1 5 3 |
| 输出 | 15 |
| 说明 | 服务3启动依赖服务2,服务2启动依赖服务1,由于服务1,2,3自身加载需要消耗5s,所以5+5+5=15,需要等待15s后可以对服务3进行集成测试 |
| 输入 | 3 5 0 0 1 10 1 1 0 11 2 |
| 输出 | 26 |
| 说明 | 服务2启动依赖服务1和服务3,服务3启动需要依赖服务1,服务1,2,3自身加载需要消耗5s,10s,11s,所以5+10+11=26s,需要等待26s后可以对服务2进行集成测试。 |
| 输入 | 4 2 0 0 0 0 3 0 0 1 1 4 0 1 1 1 5 4 |
| 输出 | 12 |
| 说明 | 服务3启动依赖服务1和服务2,服务4启动需要依赖服务1,2,3,服务1,2,3自身加载需要消耗2s,3s,4s,5s,所以3+4+5=12s(因为服务1和服务2可以同时启动),要等待12s后可以对服务4进行集成测试。 |
| 输入 | 5 1 0 0 0 0 0 2 0 0 0 1 1 3 0 0 1 1 0 4 0 0 0 1 1 5 5 |
| 输出 | 11 |
| 说明 | 服务3启动依赖服务1和服务2,服务4启动需要依赖服务1,2,服务5启动需要依赖服务3,5,服务1,2,3,4,5自身加载需要消耗1s,2s,3s,4s,5s,所以2+4+5=11s(因为服务1和服务2可以同时启动,服务3和服务4可以同时启动),要等待11s后可以对服务5进行集成测试。 |
题目解析
本题看上去很像拓扑排序,但是拓扑排序并不是解决本题的最佳方案。
本题最佳解题思路是,利用递归,求解要求的服务点的启动时间,具体思路如下:
比如用例3图示如下:
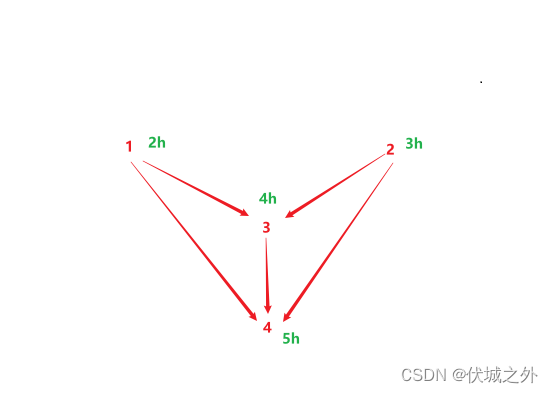
现在要求解服务4的启动时间,其实就是:
服务4的启动时间 = max(服务1启动时间, 服务2启动时间, 服务3启动时间) + 本身启动时间
其中,服务1,服务2没有前置服务,因此他们的启动时间就是本身启动时间。
而,服务3有前置服务,因此服务3的启动时间 = max(服务1启动时间, 服务2启动时间)+ 本身启动时间
因此,服务3的启动时间 = max(2, 3) + 4 = 7
进而,服务4的启动时间 = max(2, 3, 7) + 5 = 12
这里提供一个测试用例:
4
2 0 0 1
0 3 0 0
0 1 1 0
0 1 1 1
1
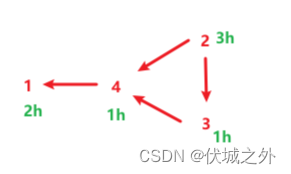
输出应该是7
再提高一个测试用例:
4
5 0 0 0
0 1 0 0
0 1 1 0
1 0 1 3
4
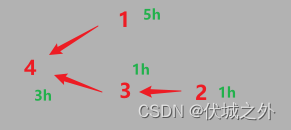
输出应该是8
再补充一个测试用例:
6
6 0 0 0 0 0
1 1 0 0 0 0
0 0 5 1 0 1
0 0 0 2 0 0
0 1 1 0 3 1
0 0 0 0 0 3
5
输出应该是11
图示如下
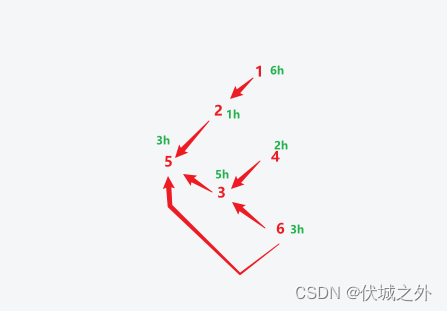
依赖关系如下:
5 依赖于 2,3服务启动完成;
– 2 依赖于 1 服务启动完成;
– 1 不依赖于其他服务
– 3 依赖于 4,6服务启动完成;
– 4 不依赖于其他服务
– 6 不依赖于其他服务
我们假设当前时刻为0,然后1,4,6同时开始启动
0时刻:1,4,6启动中
1时刻:1,4,6启动中
2时刻:1,6启动中,4启动完成
3时刻:1 启动中,6启动完成,因此该时刻3服务可以启动了
4时刻:1,3启动中
5时刻:1,3启动中
6时刻:3启动中,1启动完成,因此该时刻2服务可以启动了
7时刻:3启动中,2启动完成
8时刻:3启动完成,因此该时刻5服务可以启动了
9时刻:5启动中
10时刻:5启动中
11时刻:5启动完成
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n;
let cache;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
n = lines[0] - 0;
}
if (n && lines.length === n + 2) {
lines.shift();
const k = lines.pop();
const matrix = lines.map((line) => line.split(" ").map(Number));
cache = new Array(n);
console.log(getResult(matrix, k));
lines.length = 0;
}
});
function getResult(matrix, k) {
return dfs(k - 1, matrix);
}
function dfs(k, matrix) {
// cache用于记录每个服务所需要时间,避免多个子服务依赖同一个父服务时,对父服务启动时间的重复递归求解
if (cache[k] != undefined) return cache[k];
const preK = matrix[k];
let maxPreTime = 0;
for (let i = 0; i < preK.length; i++) {
if (i != k && preK[i] != 0) {
maxPreTime = Math.max(maxPreTime, dfs(i, matrix));
}
}
cache[k] = matrix[k][k] + maxPreTime;
return cache[k];
}
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int[] cache;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
cache = new int[n];
Arrays.fill(cache, -1);
int[][] matrix = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = sc.nextInt();
}
}
int k = sc.nextInt();
System.out.println(getResult(matrix, n, k));
}
public static int getResult(int[][] matrix, int n, int k) {
return dfs(k - 1, matrix);
}
public static int dfs(int k, int[][] matrix) {
// cache用于记录每个服务所需要时间,避免多个子服务依赖同一个父服务时,对父服务启动时间的重复递归求解
if (cache[k] != -1) return cache[k];
int[] preK = matrix[k];
int maxPreTime = 0;
for (int i = 0; i < preK.length; i++) {
if (i != k && preK[i] != 0) {
maxPreTime = Math.max(maxPreTime, dfs(i, matrix));
}
}
cache[k] = matrix[k][k] + maxPreTime;
return cache[k];
}
}
Python算法源码
# 输入获取
n = int(input())
matrix = [list(map(int, input().split())) for i in range(n)]
k = int(input())
cache = [-1]*n
def dfs(k, matrix):
# cache用于记录每个服务所需要时间,避免多个子服务依赖同一个父服务时,对父服务启动时间的重复递归求解
if cache[k] != -1:
return cache[k]
preK = matrix[k]
maxPreTime = 0
for i in range(len(preK)):
if i != k and preK[i] != 0:
maxPreTime = max(maxPreTime, dfs(i, matrix))
cache[k] = matrix[k][k] + maxPreTime
return cache[k]
# 算法入口
def getResult(matrix, k):
return dfs(k - 1, matrix)
# 算法调用
print(getResult(matrix, k))
免责声明:
评论0