题目描述
日志采集是运维系统的的核心组件。日志是按行生成,每行记做一条,由采集系统分批上报。
- 如果上报太频繁,会对服务端造成压力;
- 如果上报太晚,会降低用户的体验;
- 如果一次上报的条数太多,会导致超时失败。
为此,项目组设计了如下的上报策略:
- 每成功上报一条日志,奖励1分
- 每条日志每延迟上报1秒,扣1分
- 积累日志达到100条,必须立即上报
给出日志序列,根据该规则,计算首次上报能获得的最多积分数。
输入描述
按时序产生的日志条数 T1,T2…Tn,其中 1<=n<=1000,0<=Ti<=100
输出描述
首次上报最多能获得的积分数
用例
| 输入 |
|
| 输出 | 98 |
| 说明 | T1 时刻上报得 1 分 T2 时刻上报得98分,最大 T3 时刻上报得 0 分 |
| 输入 | 50 60 1 |
| 输出 | 50 |
| 说明 | 如果第1个时刻上报,获得积分50。如果第2个时刻上报,最多上报100条,前50条延迟上报1s,每条扣除1分,共获得积分为 100-50=50 |
| 输入 | 3 7 40 10 60 |
| 输出 | 37 |
| 说明 |
T1时刻上报得3分 T2时刻上报得7分 T3时刻上报得37分,最大 T4时刻上报得-3分 T5时刻上报,因为已经超了100条限制,所以只能上报100条,得-23分 |
题目解析
用例1意思是:
如果在T1时刻上报日志,由于只有1条日志,因此可得1分。
如果在T2时刻上报日志,由于T1时刻产生的1条日志延迟了1秒上报,因此要扣1分,到了T2时刻可以上报1+98条日志,可得99分,因此99-1=98分。
如果在T3时刻上报日志,则T1日志延迟了2s,要扣1*2分,T2日志延迟了1s,要扣98*1分,T3时刻可以上报100条日志,可得100分,因此100-2-98=0分。
我的解题思路如下:
这种前后数据具有依赖关系,一般都是用动态规划DP解决。
首先,我用前缀和思路,将每个时刻,可得的正向分计算出来缓存进dp数组中。所谓正向分,比如T2时刻积累了99条日志,那么就应该得到99分。这是正向得分。但是最终得分还需要扣除延迟上报的负向得分。比如T2时刻上报日志的话,则T1时刻产生的每条日志都需要扣除1分,这是负向得分。因此T2时刻的最终得分是:正向得分 – 负向得分 = 99 – 1 = 98分。
每个时刻都有两种选择,上报、不上报。如果某时刻选择不上报,则会正向得分、负向得分不会清零,即会累加给下一个时刻,如果某时刻选择上报了,则对应的正向得分和负向得分都会清零。
需要注意的是,当日志累计到100条或以上时,则必须要上报,这意味着会产生一次得分清零。
2023.04.22 优化一下解析说明
以用例3为例
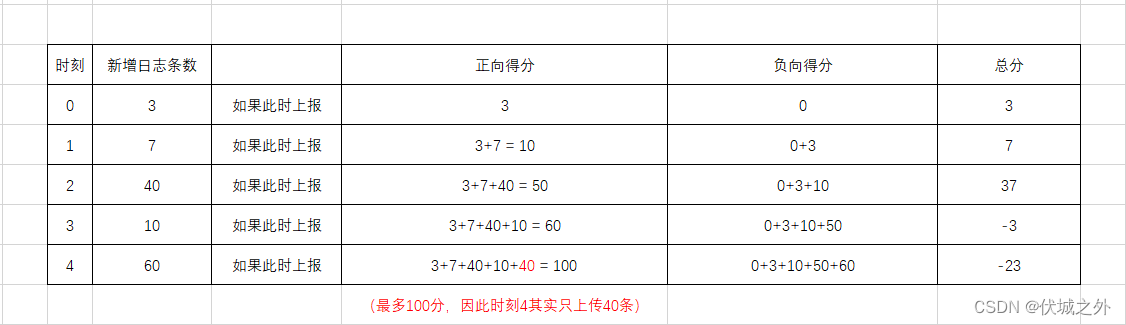
dp记录正向得分,dp[i] = dp[i-1] + arr[i],即前缀和计算
delay记录负向得分,delay[i] = delay[i-1] + dp[i-1],如下图所示

score记录总分,score[i] = dp[i] – delay[i]
另外当日志积累到100条时,就必须上报100条,比如上面时刻4,虽然新增了60条,但是实际上这60条只能上报40条
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const arr = line.split(" ").map(Number);
const dp = [arr[0]]; // dp[i]表示:第i时刻可得的正向分
const delay = [0]; // delay[i]表示:第i时刻被扣除的负向分
const score = [arr[0]]; // score[i]表示:第i时刻最终得分
for (let i = 1; i < arr.length; i++) {
dp[i] = Math.min(100, dp[i - 1] + arr[i]); // 最多上报100条
delay[i] = delay[i - 1] + dp[i - 1];
score[i] = dp[i] - delay[i];
// 达到100条时必须上报,此时完成首次上报,结束循环
if (dp[i] >= 100) break;
}
console.log(Math.max.apply(null, score));
});
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Integer[] arr =
Arrays.stream(sc.nextLine().split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
System.out.println(getResult(arr));
}
public static int getResult(Integer[] arr) {
int n = arr.length;
// dp[i]表示:第i时刻可得的正向分
int[] dp = new int[n];
dp[0] = arr[0];
// delay[i]表示:第i时刻被扣除的负向分
int[] delay = new int[n];
delay[0] = 0;
// score[i]表示:第i时刻最终得分
int[] score = new int[n];
score[0] = arr[0];
for (int i = 1; i < n; i++) {
dp[i] = Math.min(100, dp[i - 1] + arr[i]); // 最多上报100条
delay[i] = delay[i - 1] + dp[i - 1];
score[i] = dp[i] - delay[i];
// 达到100条时必须上报,此时完成首次上报,结束循环
if (dp[i] >= 100) break;
}
return Arrays.stream(score).max().getAsInt();
}
}
Python算法源码
# 输入获取
arr = list(map(int, input().split()))
# 算法入口
def getResult(arr):
n = len(arr)
# dp[i]表示:第i时刻可得的正向分
dp = [0] * n
# delay[i]表示:第i时刻被扣除的负向分
delay = [0] * n
# score[i]表示:第i时刻最终得分
score = [0] * n
dp[0] = arr[0]
score[0] = arr[0]
for i in range(1, n):
dp[i] = min(100, dp[i - 1] + arr[i]) # 最多上报100条
delay[i] = delay[i - 1] + dp[i - 1]
score[i] = dp[i] - delay[i]
# 达到100条时必须上报,此时完成首次上报,结束循环
if dp[i] >= 100:
break
print(max(score))
# 调用算法
getResult(arr)
免责声明:
评论0