题目描述
小明负责维护项目下的代码,需要查找出重复代码,用以支撑后续的代码优化,请你帮助小明找出重复的代码。
重复代码查找方法:以字符串形式给定两行代码(字符串长度 1 < length <= 100,由英文字母、数字和空格组成),找出两行代码中的最长公共子串。
注:如果不存在公共子串,返回空字符串
输入描述
输入的参数text1, text2分别表示两行代码
输出描述
输出任一最长公共子串
用例
| 输入 | hello123world hello123abc4 |
| 输出 | hello123 |
| 说明 | 无 |
| 输入 | private_void_method public_void_method |
| 输出 | _void_method |
| 说明 | 无 |
| 输入 | hiworld hiweb |
| 输出 | hiw |
| 说明 | 无 |
题目解析
本题可以使用动态规划求解,下面解释下本题动态规划解题思路。
动态规划,一般是将大问题分解为规模更小的相同的子问题,如果子问题依旧很难求解,则继续分解,直到规模小到子问题可以被轻松求解。
比如上面求两个字符串的最长公共子串,如果两个字符串很长,那么我们将很难一下子发现最长公共子串,那么我们可以只看两个字符串的部分范围,比如字符串str1,只看0~i范围,字符串str2,只看0~j范围,然后求解str1的0~i范围和str2的0~j范围的最长公共子串,最简单就是str1的0~0范围,即空串,和任意str2范围的最长公共子串都是空串,接着我们可以慢慢扩大str1的范围。
可能上面说的还比较抽象,我们可以用一个二维数组dp来描述上面逻辑。
dp[i][j] 表示的是,str1的0~i范围 和 str2的0~j范围 的公共子串的长度
初始时,我们可以得出如下二维矩阵
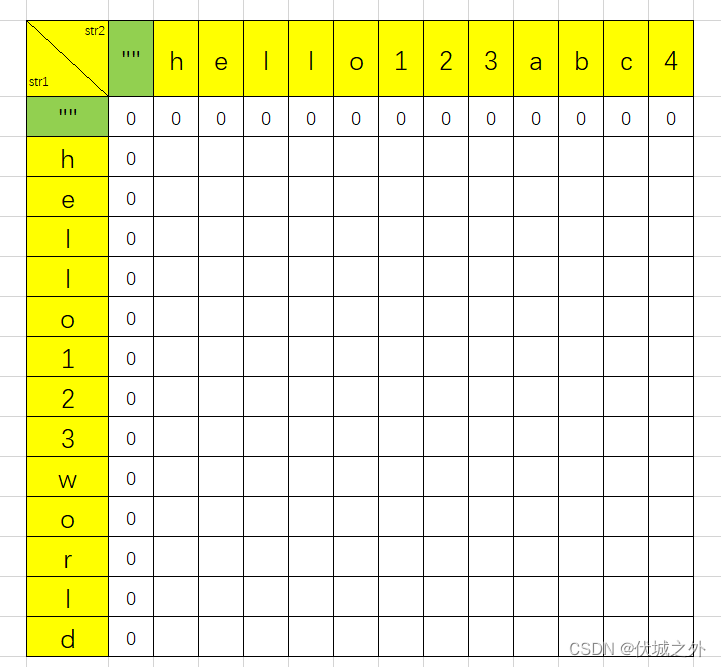
即str1取0~0,即空串时,和任意str2范围的公共子串的长度都是0。
同理,str2取0~0,即空串时,和任意str1范围的公共子串的长度都是0。
接下来, str1取0~1范围(即h),和str2取0~1范围(即h),的公共子串其实就是h,因此长度为1。如下图所示
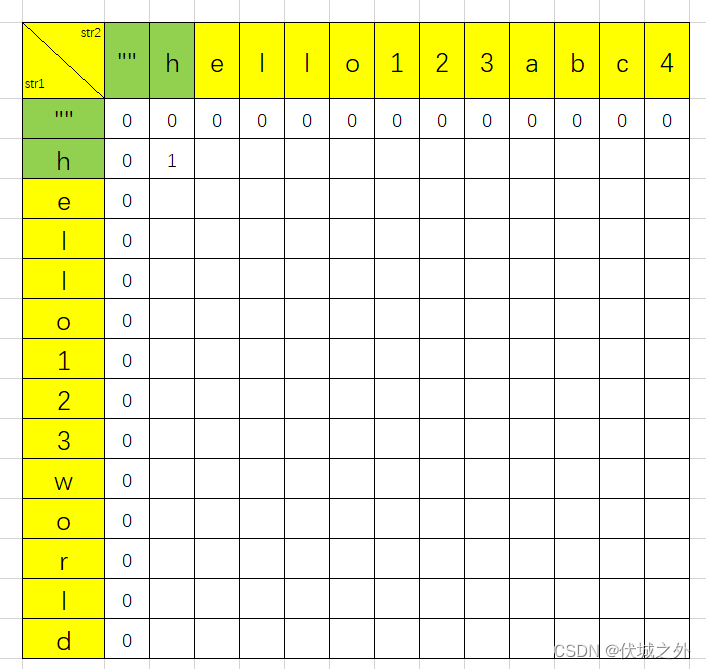
但是上面公共子串长度求解,也可以看成是,str1扩大范围新增的h,和str2扩大范围新增的h相同,因此出现了公共子串,那么就相当于在str1未扩大范围前(即空串时),和str2未扩大范围前(即空串时),的公共子串长度的基础上+1。
即:dp[1][1] = dp[0][0] + 1
进一步分析,其实可得出状态转移方程:
if(str1[i] === str2[j]) dp[i][j] = dp[i-1][j-1] + 1
再接下来, str1还是取0~1范围(即h),和str2取0~2范围(即he),
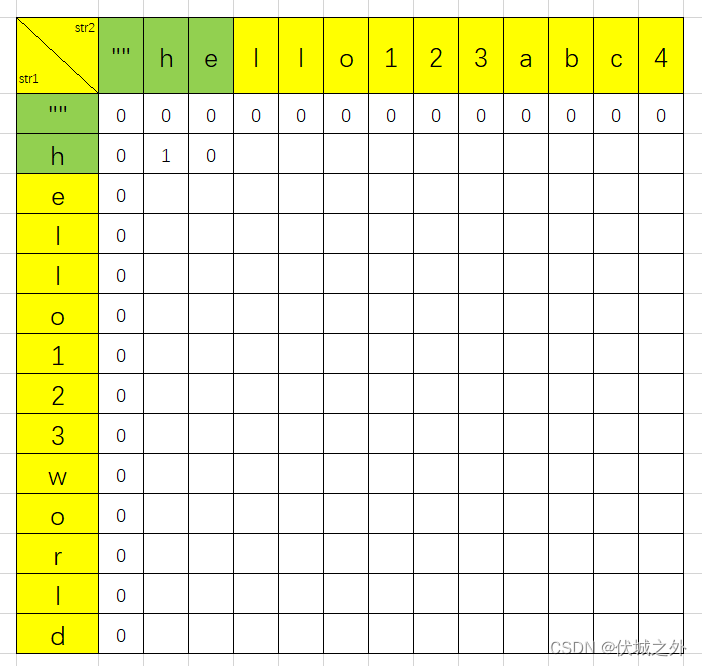
此时str1还是相当于新增h,而str2相当于新增e,新增部分不相同,所以此处没有增长前面基础上得到的公共子串的长度。
那么此时相当于 if(str1[i] !== str2[j]) dp[i][j] = dp[i-1][j-1] + 0,
但是这种思路是错误的,因为当str1,str2新增范围字符不同时,意味着公共子串的中断,我们应该将此时的dp[i][j]置为0,这样才能防止dp[i+1][j+1]对应的字符相同时,继承前面的公共子串长度。
请看下面错误例子
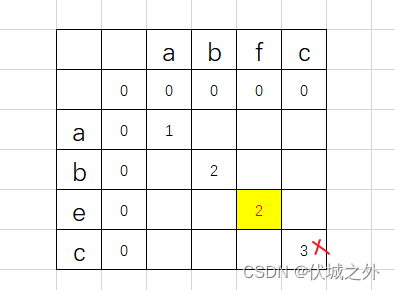
正确例子应该是
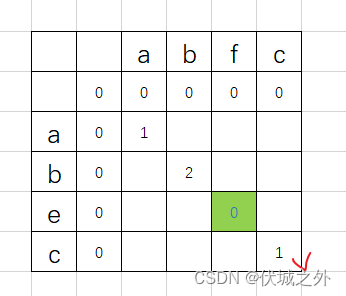
因此正确的动态规划状态转移方程是:
- dp[i][0] = 0
- dp[0][j] = 0
- if(str1[i] === str2[j]) dp[i][j] = dp[i-1][j-1] + 1 else dp[i][j] = 0
但是此题并不是让我们求解最长的公共子串的长度,而是求出任一最长公共子串。因此我们可以在遍历求解上面二维矩阵每一个元素时,记录下公共子串最大的长度值,比如下面例子中,求解到黄色元素dp[2][2]时,得到了目前最大的公共子串长度2,
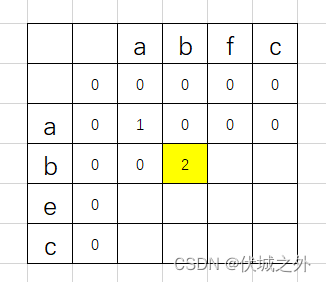
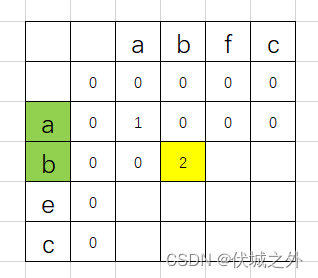
因此我们可以从任一维度来获取这个公共子串,比如从列维度,相当于 str2.slice( j – maxLen, j),其中j对应dp[i][j]中的j。maxLen=dp[i][j]。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
const str1 = lines[0];
const str2 = lines[1];
console.log(getResult(str1, str2));
lines.length = 0;
}
});
function getResult(str1, str2) {
const n = str1.length;
const m = str2.length;
const dp = new Array(n + 1).fill(0).map(() => new Array(m + 1).fill(0));
let max = 0;
let ans = "";
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
if (str1[i - 1] === str2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
if (dp[i][j] > max) {
max = dp[i][j];
ans = str1.slice(i - max, i);
}
} else {
dp[i][j] = 0;
}
}
}
return ans;
}
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str1 = sc.nextLine();
String str2 = sc.nextLine();
System.out.println(getResult(str1, str2));
}
public static String getResult(String str1, String str2) {
int n = str1.length();
int m = str2.length();
int[][] dp = new int[n + 1][m + 1];
int max = 0;
String ans = "";
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
if (dp[i][j] > max) {
max = dp[i][j];
ans = str1.substring(i - max, i);
}
} else {
dp[i][j] = 0;
}
}
}
return ans;
}
}
Python算法源码
# 输入获取
str1 = input()
str2 = input()
# 算法入口
def getResult(str1, str2):
n = len(str1)
m = len(str2)
dp = [[0 for i in range(m + 1)] for j in range(n + 1)]
maxV = 0
ans = ""
for i in range(1, n + 1):
for j in range(1, m + 1):
if str1[i - 1] == str2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
if dp[i][j] > maxV:
maxV = dp[i][j]
ans = str1[(i - maxV):i]
else:
dp[i][j] = 0
return ans
# 算法调用
print(getResult(str1, str2))
免责声明:
评论0