题目描述
有一批箱子(形式为字符串,设为str),
要求将这批箱子按从上到下以之字形的顺序摆放在宽度为 n 的空地,请输出箱子的摆放位置。
例如:箱子ABCDEFG,空地宽度为3,摆放结果如图:
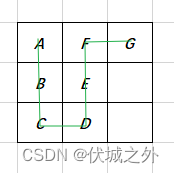
则输出结果为:AFGBECD
输入描述
输入一行字符串,通过空格分隔,前面部分为字母或数字组成的字符串str,表示箱子;
后面部分为数字n,表示空地的宽度。例如:ABCDEFG 3
输出描述
箱子摆放结果,如题目示例所示
AFGBECD
备注
- 请不要在最后一行输出额外的空行
- str只包含字母和数字,1 <= len(str) <= 1000
- 1 <= n <= 1000
用例
| 输入 | ABCDEFG 3 |
| 输出 | AFGBECD |
| 说明 |
题目解析
我的解题思路如下:
首先定义一个不定宽的二维矩阵,JS的话很简单,Java的话需要定义为List<List>结构,这个二维矩阵的高度就是给定的空地的n大小,即用例对应的初始二维矩阵应该如下
{
{},
{},
{}
}
然后,遍历字符串的每一个字符,比如用例中ABCDEFG,首先A被插入二维矩阵的第0行,即字符A在字符串中的索引 i % n 的值,比如A字符索引为i=0,n=3, 因此插入行为 i % n = 0
{
{A},
{},
{}
}
遍历B,插入二维矩阵第1行,即 i=1 , n =3, i % n = 1
{
{A},
{B},
{}
}
遍历C,插入二维矩阵的第2行,即 i=2, n=3, i%n=2
{
{A},
{B},
{C}
}
下面到关键点了,遍历D,应该插入二维矩阵的第几行呢?按照前面公式 i=3,n=3,插入行应该是第 i % n = 0 行。
但是实际上,应该要是第2行,如下面所示
{
{A},
{B},
{C,D}
}
因此,此时插入行的公式应该变为 插入行 = n – 1 – (i%n) = 3-1-0 = 2
后面E、F的插入都遵循该公式
{
{A,F},
{B,E},
{C,D}
}
但是遍历到G时,G的索引i = 6,n=3, i % n = 0,那么此时G应该插入哪一行呢?按照前面的公式,应该插入n – 1 – (i%n) = 3-1-0 = 2,但是实际上应该插入第0行,如下所示
{
{A,F,G},
{B,E},
{C,D}
}
此时,我们可以总结出,遍历的字符插入到二维矩阵的行数和其索引有关,索引和行数的转换方程有两个:
- 行数 = n – 1 – (i%n)
- 行数 = i % n
初始时,用公式:行数 = i % n,
当遇到 i % n ==0时,变换公式为:行数 = n – 1 – (i%n),
当遇到 i%n==0时,再变换公式为:行数 = i % n,
当遇到 i % n ==0时,变换公式为:行数 = n – 1 – (i%n),
当遇到 i%n==0时,再变换公式为:行数 = i % n,
…….
因此我们可以用一个reverse来标记,
当reverse=true,用公式:行数 = i % n
当reverse=false,用公式:行数 = n – 1 – (i%n)
而reverse变化的条件就是i % n ==0,每遇到i % n ==0,reverse = !reverse
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const [str, n] = line.split(" ");
getResult(str, n - 0);
});
function getResult(str, n) {
const len = str.length;
const matrix = new Array(n).fill(0).map(() => new Array());
let reverse = true;
for (let i = 0; i < len; i++) {
k = i % n;
if (k === 0) reverse = !reverse;
if (reverse) k = n - 1 - k;
matrix[k].push(str[i]);
}
matrix.forEach((arr) => console.log(arr.join("")));
}
Java算法源码
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str = sc.next();
int n = sc.nextInt();
getResult(str, n);
}
public static void getResult(String str, int n) {
ArrayList<ArrayList<Character>> matrix = new ArrayList<>();
for (int i = 0; i < n; i++) matrix.add(new ArrayList<>());
boolean reverse = true;
for (int i = 0; i < str.length(); i++) {
int k = i % n;
if (k == 0) reverse = !reverse;
if (reverse) k = n - 1 - k;
matrix.get(k).add(str.charAt(i));
}
for (ArrayList<Character> list : matrix) {
StringBuilder sb = new StringBuilder();
for (Character character : list) {
sb.append(character);
}
System.out.println(sb);
}
}
}
Python算法源码
# 输入获取
s, n = input().split()
# 算法入口
def getResult(s, n):
n = int(n)
matrix = [[] for i in range(n)]
reverse = True
for i in range(len(s)):
k = i % n
if k == 0:
reverse = not reverse
if reverse:
k = n - 1 - k
matrix[k].append(s[i])
for arr in matrix:
print("".join(arr))
# 算法调用
getResult(s, n)
免责声明:
评论0