题目描述
Jungle 生活在美丽的蓝鲸城,大马路都是方方正正,但是每天马路的封闭情况都不一样。
地图由以下元素组成:
1)”.” — 空地,可以达到;
2)”*” — 路障,不可达到;
3)”S” — Jungle的家;
4)”T” — 公司.
其中我们会限制Jungle拐弯的次数,同时Jungle可以清除给定个数的路障,现在你的任务是计算Jungle是否可以从家里出发到达公司。
输入描述
输入的第一行为两个整数t,c(0 ≤ t,c ≤ 100),t代表可以拐弯的次数,c代表可以清除的路障个数。
输入的第二行为两个整数n,m(1 ≤ n,m ≤ 100),代表地图的大小。
接下来是n行包含m个字符的地图。n和m可能不一样大。
我们保证地图里有S和T。
输出描述
输出是否可以从家里出发到达公司,是则输出YES,不能则输出NO。
用例
| 输入 | 2 0 5 5 ..S.. ****. T…. ****. ….. |
| 输出 | YES |
| 说明 | 无 |
| 输入 | 1 2 5 5 .*S*. ***** ..*.. ***** T…. |
| 输出 | NO |
| 说明 | 该用例中,至少需要拐弯1次,清除3个路障,所以无法到达 |
题目解析
用例1图示
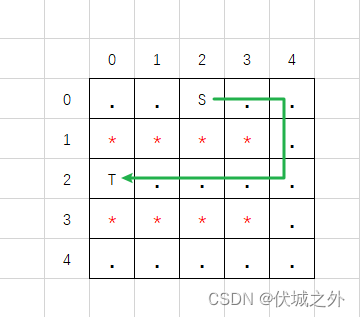
用例2图示
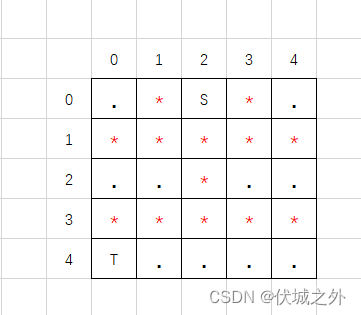
本题和迷宫问题很像,都可以使用深度优先搜索来做,相较于其他迷宫问题,本题对找终点的运动路径做了如下限制:
1、最多只能变更t次数运动方向
2、支持破壁,即清除障碍,但是最多只能破壁c次数。
因此,我们在深度优先搜索之前,需要定义两个变量:
- ut:已变更了几次运动方向
- uc:已破壁几次
如果深度优先搜索的下一步的代价是ut > t,或者uc > c,则说明下一步无法继续走了。
JavaScript算法源码
可以debug看下path中运动位置变化帮助理解
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let t, c, n, m;
let matrix;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
[t, c] = lines[0].split(" ").map(Number);
[n, m] = lines[1].split(" ").map(Number);
}
if (n && lines.length === n + 2) {
matrix = lines.slice(2).map((line) => line.split(""));
console.log(getResult());
lines.length = 0;
}
});
function getResult() {
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
if (matrix[i][j] == "S") {
return dfs(i, j, 0, 0, undefined, new Set([`${i}-${j}`]))
? "YES"
: "NO";
}
}
}
}
const offsets = [
[-1, 0, "up"],
[1, 0, "down"],
[0, -1, "left"],
[0, 1, "right"],
];
/**
* @param {*} si 当前位置横坐标
* @param {*} sj 当前位置纵坐标
* @param {*} ut 已拐弯次数
* @param {*} uc 已破壁次数
* @param {*} lastDirect 上一次运动方向,初始为undefined,表示第一次运动不会造成拐弯
* @param {*} path 行动路径,用于记录走过的位置,避免走老路
* @returns
*/
function dfs(si, sj, ut, uc, lastDirect, path) {
// 如果当前位置就是目的地,则返回true
if (matrix[si][sj] == "T") {
return true;
}
// 有四个方向选择走下一步
for (let offset of offsets) {
const [offsetX, offsetY, direct] = offset;
const newI = si + offsetX;
const newJ = sj + offsetY;
// flag1记录是否拐弯
let flag1 = false;
// flag2记录是否破壁
let flag2 = false;
// 如果下一步位置没有越界,则进一步检查
if (newI >= 0 && newI < n && newJ >= 0 && newJ < m) {
// 如果下一步位置已经走过了,则是老路,可以不走
const pos = `${newI}-${newJ}`;
if (path.has(pos)) continue;
// 如果下一步位置需要拐弯
if (lastDirect && lastDirect != direct) {
// 如果拐弯次数用完了,则不走
if (ut + 1 > t) continue;
// 否则就走
flag1 = true;
}
// 如果下一步位置需要破壁
if (matrix[newI][newJ] == "*") {
// 如果破壁次数用完了,则不走
if (uc + 1 > c) continue;
// 否则就走
flag2 = true;
}
// 记录已走过的位置
path.add(pos);
// 继续下一步递归
const res = dfs(
newI,
newJ,
ut + (flag1 ? 1 : 0), // 如果拐弯了,则已使用的拐弯次数++
uc + (flag2 ? 1 : 0), // 如果破壁了,则已使用的破壁次数++
direct,
path
);
// 如果某路径可以在给定的t,c下,到达目的地T,则返回true
if (res) return true;
// 否则,回溯
path.delete(pos);
}
}
return false;
}
Java算法源码
import java.util.HashSet;
import java.util.Scanner;
public class Main {
static int t, c, n, m;
static String[][] matrix;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
t = sc.nextInt();
c = sc.nextInt();
n = sc.nextInt();
m = sc.nextInt();
matrix = new String[n][m];
for (int i = 0; i < n; i++) {
matrix[i] = sc.next().split("");
}
System.out.println(getResult());
}
public static String getResult() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if ("S".equals(matrix[i][j])) {
HashSet<Integer> path = new HashSet<>();
path.add(i * m + j);
return dfs(i, j, 0, 0, 0, path) ? "YES" : "NO";
}
}
}
return "NO";
}
// 元素含义【行偏移,列偏移,运动方向】,运动方向:1上,2下,3左,4右
static int[][] offsets = {{-1, 0, 1}, {1, 0, 2}, {0, -1, 3}, {0, 1, 4}};
/**
* @param si 当前位置横坐标
* @param sj 当前位置纵坐标
* @param ut 已拐弯次数
* @param uc 已破壁次数
* @param lastDirect 上一次运动方向,初始为0,表示第一次运动不会造成拐弯
* @param path 行动路径,用于记录走过的位置,避免走老路
* @return 终点是否可达
*/
public static boolean dfs(int si, int sj, int ut, int uc, int lastDirect, HashSet<Integer> path) {
// 如果当前位置就是目的地,则返回true
if ("T".equals(matrix[si][sj])) {
return true;
}
// 有四个方向选择走下一步
for (int[] offset : offsets) {
int direct = offset[2];
int newI = si + offset[0];
int newJ = sj + offset[1];
// flag1记录本次运动是否拐弯
boolean flag1 = false;
// flag2记录本次运动是否破壁
boolean flag2 = false;
// 如果下一步位置没有越界,则进一步检查
if (newI >= 0 && newI < n && newJ >= 0 && newJ < m) {
// 如果下一步位置已经走过了,则是老路,可以不走
int pos = newI * m + newJ;
if (path.contains(pos)) continue;
// 如果下一步位置需要拐弯
if (lastDirect != 0 && lastDirect != direct) {
// 如果拐弯次数用完了,则不走
if (ut + 1 > t) continue;
// 否则就走
flag1 = true;
}
// 如果下一步位置需要破壁
if ("*".equals(matrix[newI][newJ])) {
// 如果破壁次数用完了,则不走
if (uc + 1 > c) continue;
// 否则就走
flag2 = true;
}
// 记录已走过的位置
path.add(pos);
// 继续下一步递归
boolean res = dfs(newI, newJ, ut + (flag1 ? 1 : 0), uc + (flag2 ? 1 : 0), direct, path);
// 如果某路径可以在给定的t,c下,到达目的地T,则返回true
if (res) return true;
// 否则,回溯
path.remove(pos);
}
}
return false;
}
}
Python算法源码
t, c = map(int, input().split())
n, m = map(int, input().split())
matrix = []
for i in range(n):
matrix.append(input())
offsets = ((-1, 0, "up"), (1, 0, "down"), (0, -1, "left"), (0, 1, "right"))
def dfs(si, sj, ut, uc, lastDirect, path):
"""
:param si: 当前位置横坐标
:param sj: 当前位置纵坐标
:param ut: 已拐弯次数
:param uc: 已破壁次数
:param lastDirect: 上一次运动方向,初始为undefined,表示第一次运动不会造成拐弯
:param path: 行动路径,用于记录走过的位置,避免走老路
:return:
"""
# 如果当前位置就是目的地,则返回true
if matrix[si][sj] == "T":
return True
# 有四个方向选择走下一步
for offset in offsets:
offsetX, offsetY, direct = offset
newI = si + offsetX
newJ = sj + offsetY
# flag1记录是否拐弯
flag1 = False
# flag2记录是否破壁
flag2 = False
# 如果下一步位置没有越界,则进一步检查
if 0 <= newI < n and 0 <= newJ < m:
# 如果下一步位置已经走过了,则是老路,可以不走
pos = f'{newI}-{newJ}'
if pos in path:
continue
# 如果下一步位置需要拐弯
if lastDirect is not None and lastDirect != direct:
# 如果拐弯次数用完了,则不走
if ut + 1 > t:
continue
# 否则就走
flag1 = True
# 如果下一步位置需要破壁
if matrix[newI][newJ] == "*":
# 如果破壁次数用完了,则不走
if uc + 1 > c:
continue
# 否则就走
flag2 = True
# 记录已走过的位置
path.add(pos)
# 继续下一步递归
# 如果拐弯了,则已使用的拐弯次数ut++
# 如果破壁了,则已使用的破壁次数uc++
res = dfs(newI, newJ, ut + (1 if flag1 else 0), uc + (1 if flag2 else 0), direct, path)
# 如果某路径可以在给定的t,c下,到达目的地T,则返回true
if res:
return True
# 否则,回溯
path.remove(pos)
return False
def getResult():
for i in range(n):
for j in range(m):
if matrix[i][j] == "S":
return "YES" if dfs(i, j, 0, 0, None, {f'{i}-{j}'}) else "NO"
print(getResult())
免责声明:
1、IT资源小站为非营利性网站,全站所有资料仅供网友个人学习使用,禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享,本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题,请立即告知本站,本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体,但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员,一律视为同意网站规定,本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0