题目描述
九宫格是一款广为流传的游戏,起源于河图洛书。游戏规则是:1到9九个数字放在3×3的格子中,要求每行、每列以及两个对角线上的三数之和都等于15。
在金庸名著《射雕英雄传》中黃蓉曾给九宫格的一种解法,口诀:戴九恩一,左三右七,二四有肩,八六为足,五居中央。解法如图所示。
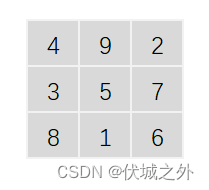
现在有一种新的玩法,给九个不同的数字,将这九个数字放在3×3的格子中,要求每行、每列以及两个对角线上的三数之积相等(三阶积幻方)。
其中一个三阶幻方如图:
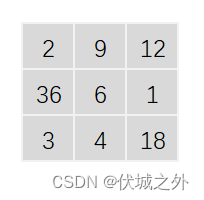
解释:每行、每列以及两个对角线上的三数之积相等,都为216。
请设计一种算法,将给定的九个数宇重新排列后,使其满足三阶积幻方的要求。排列后的九个数宇中:第1-3个数字为方格的第一行,第4-6个数宇为方格的第二行,第7-9个数字为方格的第三行。
输入描述
九个不同的数宇,每个数字之间用空格分开。
- 0 < 数字 < 10^7。
- 0 < 排列后满足要求的每行、每列以及两个对角线上的三数之积 < 2^31-1
输出描述
九个数字所有满足要求的排列,每个数字之间用空格分开。每行输出一个满足要求的排列。
要求输出的排列升序排序,即:对于排列 A(A1,A2,A3,…,A9)和排列 B(B1,B2,B3,…,B9),从排列的第1个数字开始,遇到 Ai < Bi ,则排列A < 排列B (1 ≤ j ≤ 9)。
说明:用例保证至少有一种排列组合满足条件。
用例
| 输入 | 75 36 10 4 30 225 90 25 12 |
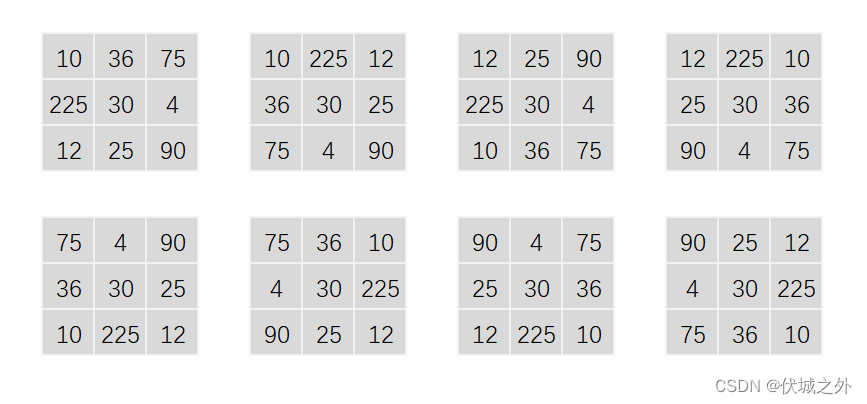
| 输出 | 10 36 75 225 30 4 12 25 90 10 225 12 36 30 25 75 4 90 12 25 90 225 30 4 10 36 75 12 225 10 25 30 36 90 4 75 75 4 90 36 30 25 10 225 12 75 36 10 4 30 225 90 25 12 90 4 75 25 30 36 12 225 10 90 25 12 4 30 225 75 36 10 |
| 说明 |
如图所示:九宫格的每行、每列以及两个对角线上的三数之积为27000。
|
| 输入 | 1 2 4 5 10 20 25 50 100 |
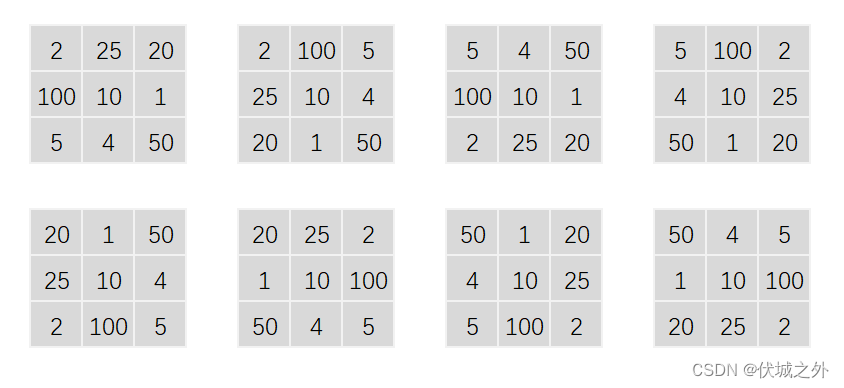
| 输出 | 2 25 20 100 10 1 5 4 50 2 100 5 25 10 4 20 1 50 5 4 50 100 10 1 2 25 20 5 100 2 4 10 25 50 1 20 20 1 50 25 10 4 2 100 5 20 25 2 1 10 100 50 4 5 50 1 20 4 10 25 5 100 2 50 4 5 1 10 100 20 25 2 |
| 说明 |
如图所示:九宫格的每行、每列以及两个对角线上的三数之和为1000。
|
题目解析
简单的全排列问题。
关于全排列的入门,可以看
练习题可以做leetcode上:
LeetCode – 46 全排列_伏城之外的博客-CSDN博客
基于回溯算法的全排列求解是一种暴力解法,即枚举出全部排列情况,因此对大数量级而言,我们应该慎用,但是本题,已经明确指出了求解9个数字的全排列,因此排列情况共有9!个,即362880个,数量级还好,因此可以使用暴力求解。
另外,求出符合要求的排列,还需要对各排列进行排序,排序是按各个数字大小来比较的,大家可以看下代码中关于排序的实现。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const arr = line.split(" ").map(Number);
getResult(arr);
});
function getResult(arr) {
const res = [];
dfs(arr, [], [], res);
res.sort((a, b) => {
for (let i = 0; i < 9; i++) {
if (a[i] !== b[i]) return a[i] - b[i];
}
return 0;
});
res.forEach((a) => console.log(a.join(" ")));
}
function dfs(arr, used, path, res) {
if (path.length === arr.length) {
if (check(path)) {
res.push([...path]);
}
return;
}
for (let i = 0; i < arr.length; i++) {
if (!used[i]) {
path.push(arr[i]);
used[i] = true;
dfs(arr, used, path, res);
used[i] = false;
path.pop();
}
}
}
function check(a) {
/**
* a0 a1 a2
* a3 a4 a5
* a6 a7 a8
*/
const r1 = a[0] * a[1] * a[2];
const r2 = a[3] * a[4] * a[5];
if (r1 != r2) return false;
const r3 = a[6] * a[7] * a[8];
if (r1 != r3) return false;
const c1 = a[0] * a[3] * a[6];
if (r1 != c1) return false;
const c2 = a[1] * a[4] * a[7];
if (r1 != c2) return false;
const c3 = a[2] * a[5] * a[8];
if (r1 != c3) return false;
const s1 = a[0] * a[4] * a[8];
if (r1 != s1) return false;
const s2 = a[2] * a[4] * a[6];
if (r1 != s2) return false;
return true;
}
Java算法源码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Integer[] arr =
Arrays.stream(sc.nextLine().split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
getResult(arr);
}
public static void getResult(Integer[] arr) {
boolean[] used = new boolean[arr.length];
LinkedList<Integer> path = new LinkedList<>();
ArrayList<Integer[]> res = new ArrayList<>();
dfs(arr, used, path, res);
res.sort(
(a, b) -> {
for (int i = 0; i < 9; i++) {
if (!Objects.equals(a[i], b[i])) return a[i] - b[i];
}
return 0;
});
for (Integer[] re : res) {
StringJoiner sj = new StringJoiner(" ");
for (Integer i : re) {
sj.add(i + "");
}
System.out.println(sj);
}
}
public static void dfs(
Integer[] arr, boolean[] used, LinkedList<Integer> path, ArrayList<Integer[]> res) {
if (path.size() == arr.length) {
if (check(path)) {
Integer[] a = path.toArray(new Integer[0]);
res.add(a);
}
return;
}
for (int i = 0; i < arr.length; i++) {
if (!used[i]) {
path.add(arr[i]);
used[i] = true;
dfs(arr, used, path, res);
used[i] = false;
path.removeLast();
}
}
}
public static boolean check(LinkedList<Integer> path) {
Integer[] a = path.toArray(new Integer[0]);
int r1 = a[0] * a[1] * a[2];
int r2 = a[3] * a[4] * a[5];
if (r1 != r2) return false;
int r3 = a[6] * a[7] * a[8];
if (r1 != r3) return false;
int c1 = a[0] * a[3] * a[6];
if (r1 != c1) return false;
int c2 = a[1] * a[4] * a[7];
if (r1 != c2) return false;
int c3 = a[2] * a[5] * a[8];
if (r1 != c3) return false;
int s1 = a[0] * a[4] * a[8];
if (r1 != s1) return false;
int s2 = a[2] * a[4] * a[6];
if (r1 != s2) return false;
return true;
}
}
Python算法源码
# 输入获取
arr = list(map(int, input().split()))
# 算法入口
def getResult(arr):
res = []
dfs(arr, [False for i in range(len(arr))], [], res)
res.sort(key=lambda x: (x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7], x[8]))
for a in res:
print(" ".join(map(str, a)))
# 全排列求解
def dfs(arr, used, path, res):
if len(path) == len(arr):
if check(path):
res.append(path[:])
return
for i in range(len(arr)):
if not used[i]:
path.append(arr[i])
used[i] = True
dfs(arr, used, path, res)
used[i] = False
path.pop()
# 检查排列a是否符合 每行、每列、两个对角线的乘积相同
def check(a):
r1 = a[0] * a[1] * a[2]
r2 = a[3] * a[4] * a[5]
if r1 != r2:
return False
r3 = a[6] * a[7] * a[8]
if r1 != r3:
return False
c1 = a[0] * a[3] * a[6]
if r1 != c1:
return False
c2 = a[1] * a[4] * a[7]
if r1 != c2:
return False
c3 = a[2] * a[5] * a[8]
if r1 != c3:
return False
s1 = a[0] * a[4] * a[8]
if r1 != s1:
return False
s2 = a[2] * a[4] * a[6]
if r1 != s2:
return False
return True
# 调用算法
getResult(arr)
免责声明:
评论0