题目描述
现有一个CPU和一些任务需要处理,已提前获知每个任务的任务ID、优先级、所需执行时间和到达时间。
CPU同时只能运行一个任务,请编写一个任务调度程序,采用“可抢占优先权调度”调度算法进行任务调度,规则如下:
- 如果一个任务到来时,CPU是空闲的,则CPU可以运行该任务直到任务执行完毕。但是如果运行中有一个更高优先级的任务到来,则CPU必须暂停当前任务去运行这个优先级更高的任务;
- 如果一个任务到来时,CPU正在运行一个比他优先级更高的任务时,新到达的任务必须等待;
- 当CPU空闲时,如果还有任务在等待,CPU会从这些任务中选择一个优先级最高的任务执行,相同优先级的任务选择到达时间最早的任务。
输入描述
输入有若干行,每一行有四个数字(均小于10^8),分别为任务ID,任务优先级,执行时间和到达时间。
每个任务的任务ID不同,优先级数字越大优先级越高,并且相同优先级的任务不会同时到达。
输入的任务已按照到达时间从小到大排序,并且保证在任何时间,处于等待的任务不超过10000个。
输出描述
按照任务执行结束的顺序,输出每个任务的任务ID和对应的结束时间。
用例
| 输入 | 1 3 5 1 2 1 5 10 3 2 7 12 4 3 2 20 5 4 9 21 6 4 2 22 |
| 输出 | 1 6 3 19 5 30 6 32 4 33 2 35 |
| 说明 | 无 |
题目解析
用例图示如下
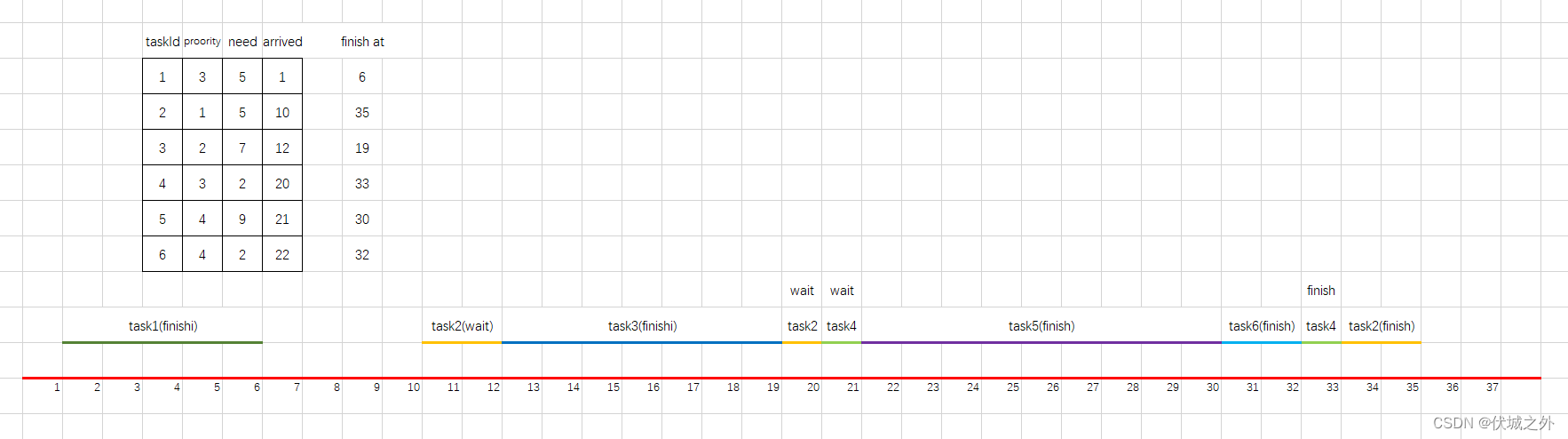
task1在1时刻到达,此时CPU空闲,因此执行task1,task1需要执行5个时间,而执行期间没有新任务加入,因此task1首先执行完成,结束时刻是6。
task2在10时刻达到,此时CPU空闲,因此执行task2,task2需要执行5个时间,但是在task2执行到12时刻时,有新任务task3加入,且优先级更高,因此task2让出执行权,task2还需要5-(12-10)= 3 个时间才能执行完,task2进入等待队列。
task3在12时刻到达,此时CPU正在执行task2,但是由于task3的优先级高于task2,因此task3获得执行权开始执行,task3需要7个时间,而在下一个任务task4会在20时刻到达,因此task3可以执行完,结束时刻是19。
task3执行结束时刻是19,而task4到达时间是20,因此中间有一段CPU空闲期,而等待队列中还有一个task2等待执行,因此此时CPU会调出task2继续执行,但是只能执行1时间,因此task2还需要3 – 1 = 2个时间才能执行完。
task4在20时刻到达,此时CPU正在执行task2,但是由于task4的优先级更高,因此task4获得执行权开始执行,task2重回等待队列,task4需要2个时间,但是执行到时刻21时,task5到达了,且优先级更高,因此task4还需2 – (21-20) = 1 个时间才能执行完,task4进入等待队列。
此时等待队列有两个任务task2,task4,因此需要按照优先级排序,优先级高的在队头,因此queue = [task4, task2]
task5在21时刻到达,此时CPU正在执行task4,但是task5的优先级更高,因此task5获得执行权开始执行,task4进入等待队列,task5需要9个时间,但是执行到时刻22时,task6到达了,但是task6的优先级和task5相同,因此task5执行不受影响,task5会在21 + 9 = 30 时刻执行完成。
而task6则进入等待队列,有新任务进入队列后,就要按优先级重新排序,优先级高的在队头,因此queue = [task6, task4, task2]。
此时所有任务已经遍历完,我们检查等待队列是否有任务,若有,则此时任务队列中的任务必然是按优先级降序的,因此我们依次取出队头任务,在上一次结束时刻基础上添加需要的时间,就是新的结束时刻,比如
task6出队,上一次结束时刻是30,因此task6的结束时刻 = 30 + 2 = 32,新的结束时刻变为32
task4出队,上一次结束时刻是32,因此task4的结束时刻 = 32 + 1 = 33,新的结束时刻变为33
task2出队,上一次结束时刻是33,因此task2的结束时刻 = 33 + 2 = 35,新的结束时刻变为33。
本题实现的难点在于:
1、等待队列的实现
这里的等待队列其实就是优先队列,优先队列我们可以基于有序数组实现,但是有序数组实现最优先队列的时间复杂度至少O(n),算是比较高的。优先队列其实只要每次保证最高优先级的任务处于队头即可,无需实现整体有序,因此基于最大堆实现优先队列是更好的选择,最大堆每次实现优先队列,只需要O(logN)的时间复杂度,因此在处理大数量级是更具有优势,但是JS语言并没有实现基于堆结构的优先队列,因此我们需要手动实现,相较于有序数组而言,难度较大。关于基于堆的优先队列实现,请看:
2、CPU的任务执行逻辑
CPU执行某个任务时,如果有新任务加入,则我们应该比较正在执行的任务和新任务的优先级,
- 如果新任务优先级较高,则应该将正在执行的任务撤出,加入到等待队列中,然后执行新任务。
- 如果新任务优先级不高于正在执行的任务,则新任务进入等待队列,继续执行当前任务。
CPU空转期间,应该检查等待队列是否有任务,并取出最高优先级任务执行。
2023.02.19 根据网友反馈上面逻辑的通过率为20%,我重新看了一下,发现上面遗漏一个逻辑:
题目说
当CPU空闲时,如果还有任务在等待,CPU会从这些任务中选择一个优先级最高的任务执行,相同优先级的任务选择到达时间最早的任务。
而上面逻辑中遗漏考虑了相同优先级时,按照到达时间为第二优先级来安排任务执行的场景。已修复。
JavaScript算法源码
基于最大堆实现优先队列
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
if (line !== "") {
lines.push(line);
} else {
const tasks = lines.map((line) => line.split(" ").map(Number));
getResult(tasks);
lines.length = 0;
}
});
/**
*
* @param {*} tasks 二维数组,元素组数含义是[任务ID,任务优先级,执行时间,到达时间]
*/
function getResult(tasks) {
tasks = tasks.map((task) => {
return { id: task[0], priority: task[1], need: task[2], arrived: task[3] };
});
const pq = new Pqueue((a, b) =>
a.priority != b.priority ? b.priority - a.priority : a.arrived - b.arrived
);
pq.offer(tasks.shift());
let curTime = pq.peek().arrived; // curTime记录当前时刻
while (tasks.length > 0) {
const curtTask = pq.peek(); // 当前正在运行的任务curtTask
const nextTask = tasks.shift(); // 下一个任务nextTask
const curTask_endTime = curTime + curtTask.need; // 当前正在运行任务的“理想”结束时间
// 如果当前正在运行任务的理想结束时间 超过了 下一个任务的开始时间
if (curTask_endTime > nextTask.arrived) {
curtTask.need -= nextTask.arrived - curTime; // 先不看优先级,先将当前任务可以运行的时间减去
curTime = nextTask.arrived;
}
// 如果当前正在运行任务的理想结束时间 没有超过 下一个任务的开始时间,则当前任务可以执行完
else {
pq.poll();
console.log(`${curtTask.id} ${curTask_endTime}`); // 打印执行完的任务的id和结束时间
curTime = curTask_endTime;
// 如果当前任务结束时,下一次任务还没有达到,那么存在CPU空转(即idle)
if (nextTask.arrived > curTask_endTime) {
// 此时,我们应该从优先队列中取出最优先的任务出来执行,逻辑同上
while (pq.size > 0) {
const idleTask = pq.peek();
const idleTask_endTime = curTime + idleTask.need;
if (idleTask_endTime > nextTask.arrived) {
idleTask.need -= nextTask.arrived - curTime;
break;
} else {
pq.poll();
console.log(`${idleTask.id} ${idleTask_endTime}`);
curTime = idleTask_endTime;
}
}
curTime = nextTask.arrived;
}
}
pq.offer(nextTask);
}
// 所有任务都加入优先队列后,我们就可以按照优先队列的安排,顺序取出任务来执行了
while (pq.size > 0) {
const pollTask = pq.poll();
const pollTask_endTime = curTime + pollTask.need;
console.log(`${pollTask.id} ${pollTask_endTime}`);
curTime = pollTask_endTime;
}
}
// 基于堆实现优先队列
class Pqueue {
constructor(cpr) {
this.queue = [];
this.size = 0;
this.cpr = cpr;
}
swap(i, j) {
let tmp = this.queue[i];
this.queue[i] = this.queue[j];
this.queue[j] = tmp;
}
// 上浮
swim() {
let ch = this.queue.length - 1;
while (ch !== 0) {
let fa = Math.floor((ch - 1) / 2);
const ch_node = this.queue[ch];
const fa_node = this.queue[fa];
if (this.cpr(ch_node, fa_node) < 0) {
this.swap(ch, fa);
ch = fa;
} else {
break;
}
}
}
// 下沉
sink() {
let fa = 0;
while (true) {
let ch_left = 2 * fa + 1;
let ch_right = 2 * fa + 2;
let ch_max;
let ch_max_node;
const fa_node = this.queue[fa];
const ch_left_node = this.queue[ch_left];
const ch_right_node = this.queue[ch_right];
if (ch_left_node && ch_right_node) {
// 注意这里应该要>=0,因为左边优先级高
if (this.cpr(ch_left_node, ch_right_node) <= 0) {
ch_max = ch_left;
ch_max_node = ch_left_node;
} else {
ch_max = ch_right;
ch_max_node = ch_right_node;
}
} else if (ch_left_node && !ch_right_node) {
ch_max = ch_left;
ch_max_node = ch_left_node;
} else if (!ch_left_node && ch_right_node) {
ch_max = ch_right;
ch_max_node = ch_right_node;
} else {
break;
}
// 注意这里应该要>0,因为父优先级高
if (this.cpr(ch_max_node, fa_node) < 0) {
this.swap(ch_max, fa);
fa = ch_max;
} else {
break;
}
}
}
// 向优先队列中加入元素
offer(ele) {
this.queue.push(ele);
this.size++;
this.swim();
}
// 取出最高优先级元素
poll() {
this.swap(0, this.queue.length - 1);
this.size--;
const ans = this.queue.pop();
this.sink();
return ans;
}
// 只使用最高优先级元素,不取出
peek() {
return this.queue[0];
}
}
Java算法源码
Java已有专门的优先队列实现类PriorityQueue,因此我们可以直接使用它,而不需要自己实现。
import java.util.Arrays;
import java.util.LinkedList;
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
LinkedList<Task> list = new LinkedList<>();
while (sc.hasNextLine()) {
String s = sc.nextLine();
if ("".equals(s)) break;
Integer[] arr = Arrays.stream(s.split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
Task task = new Task(arr[0], arr[1], arr[2], arr[3]);
list.add(task);
}
getResult(list);
}
/**
* @param tasks 任务列表
*/
public static void getResult(LinkedList<Task> tasks) {
PriorityQueue<Task> pq =
new PriorityQueue<>(
(a, b) -> a.priority != b.priority ? b.priority - a.priority : a.arrived - b.arrived);
pq.offer(tasks.removeFirst());
int curTime = pq.peek().arrived; // curTime记录当前时刻
while (tasks.size() > 0) {
Task curtTask = pq.peek(); // 当前正在运行的任务curtTask
Task nextTask = tasks.removeFirst(); // 下一个任务nextTask
int curtTask_endTime = curTime + curtTask.need; // 当前正在运行任务的“理想”结束时间
if (curtTask_endTime > nextTask.arrived) { // 如果当前正在运行任务的理想结束时间 超过了 下一个任务的开始时间
curtTask.need -= nextTask.arrived - curTime; // 先不看优先级,先将当前任务可以运行的时间减去
curTime = nextTask.arrived;
} else { // 如果当前正在运行任务的理想结束时间 没有超过 下一个任务的开始时间,则当前任务可以执行完
pq.poll(); // 当前任务出队
System.out.println(curtTask.id + " " + curtTask_endTime); // 打印执行完的任务的id和结束时间
curTime = curtTask_endTime;
if (nextTask.arrived > curtTask_endTime) { // 如果当前任务结束时,下一次任务还没有达到,那么存在CPU空转(即idle)
while (pq.size() > 0) { // 此时,我们应该从优先队列中取出最优先的任务出来执行,逻辑同上
Task idleTask = pq.peek();
int idleTask_endTime = curTime + idleTask.need;
if (idleTask_endTime > nextTask.arrived) {
idleTask.need -= nextTask.arrived - curTime;
break;
} else {
pq.poll();
System.out.println(idleTask.id + " " + idleTask_endTime);
curTime = idleTask_endTime;
}
}
curTime = nextTask.arrived;
}
}
pq.offer(nextTask);
}
// 所有任务都加入优先队列后,我们就可以按照优先队列的安排,顺序取出任务来执行了
while (pq.size() > 0) {
Task pollTask = pq.poll();
int pollTask_endTime = curTime + pollTask.need;
System.out.println(pollTask.id + " " + pollTask_endTime);
curTime = pollTask_endTime;
}
}
}
class Task {
int id; // 任务id
int priority; // 任务优先级
int need; // 任务执行时长
int arrived; // 任务到达时刻
public Task(int id, int priority, int need, int arrived) {
this.id = id;
this.priority = priority;
this.need = need;
this.arrived = arrived;
}
}
Python算法源码
Pytho可以基于queue.PriorityQueue来实现优先队列,但是queue.PriorityQueue的自定义排序不支持函数参数传入,而是只能基于queue.PriorityQueue加入的元素的自身比较器(如__lt__和__gt__)来排序
import queue
class Task:
def __init__(self, taskId, priority, need, arrived):
self.taskId = taskId
self.priority = priority
self.need = need
self.arrived = arrived
def __gt__(self, other):
if self.priority != other.priority:
return other.priority > self.priority
else:
return self.arrived > other.arrived
# 算法入口
def getResult(tasks):
pq = queue.PriorityQueue()
pq.put(tasks.pop(0))
curTime = pq.queue[0].arrived # curTime记录当前时刻
while len(tasks) > 0:
curtTask = pq.queue[0] # 当前正在运行的任务curtTask
nextTask = tasks.pop(0) # 下一个任务nextTask
curTask_endTime = curTime + curtTask.need # 当前正在运行任务的“理想”结束时间
# 如果当前正在运行任务的理想结束时间 超过了 下一个任务的开始时间
if curTask_endTime > nextTask.arrived:
curtTask.need -= nextTask.arrived - curTime # 先不看优先级,先将当前任务可以运行的时间减去
curTime = nextTask.arrived
# 如果当前正在运行任务的理想结束时间 没有超过 下一个任务的开始时间,则当前任务可以执行完
else:
pq.get()
print(f"{curtTask.taskId} {curTask_endTime}") # 打印执行完的任务的id和结束时间
curTime = curTask_endTime
# 如果当前任务结束时,下一次任务还没有达到,那么存在CPU空转(即idle)
if nextTask.arrived > curTask_endTime:
# 此时,我们应该从优先队列中取出最优先的任务出来执行,逻辑同上
while pq.qsize() > 0:
idleTask = pq.queue[0]
idleTask_endTime = curTime + idleTask.need
if idleTask_endTime > nextTask.arrived:
idleTask.need -= nextTask.arrived - curTime
break
else:
pq.get()
print(f"{idleTask.taskId} {idleTask_endTime}")
curTime = idleTask_endTime
curTime = nextTask.arrived
pq.put(nextTask)
# 所有任务都加入优先队列后,我们就可以按照优先队列的安排,顺序取出任务来执行了
while pq.qsize() > 0:
pollTask = pq.get()
pollTask_endTime = curTime + pollTask.need
print(f"{pollTask.taskId} {pollTask_endTime}")
curTime = pollTask_endTime
# 输入获取
tasks = []
while True:
task = input()
if task == "":
getResult(tasks)
break
else:
tmp = list(map(int, task.split()))
task = Task(tmp[0], tmp[1], tmp[2], tmp[3])
tasks.append(task)
免责声明:
评论0