题目描述
张三要去外地出差,需要做核酸,需要在指定时间点前做完核酸,请帮他找到满足条件的核酸检测点。
- 给出一组核酸检测点的距离和每个核酸检测点当前的人数
- 给出张三要去做核酸的出发时间 出发时间是10分钟的倍数,同时给出张三做核酸的最晚结束时间
- 题目中给出的距离是整数,单位是公里,时间1分钟为一基本单位
去找核酸点时,有如下的限制:
- 去往核酸点的路上,每公里距离花费时间10分钟,费用是10元
- 核酸点每检测一个人的时间花费是1分钟
- 每个核酸点工作时间都是8点到20点中间不休息,核酸点准时工作,早到晚到都不检测
- 核酸检测结果可立刻知道
- 在张三去某个核酸点的路上花费的时间内,此核酸检测点的人数是动态变化的,变化规则是
- 在非核酸检测时间内,没有人排队
- 8点-10点每分钟增加3人
- 12点-14点每分钟增加10人
- 18点-20点每分钟增加20人。
- 其他时间每5分钟增加1人。
要求将所有满足条件的核酸检测点按照优选规则排序列出 :
优选规则:
- 花费时间最少的核酸检测点排在前面。
- 花费时间一样,花费费用最少的核酸检测点排在前面。
- 时间和费用一样,则ID值最小的排在前面
输入描述
H1 M1
H2 M2
N
ID1 D1 C1
ID2 D2 C2
…
IDn Dn Cn
H1: 当前时间的小时数。
M1:当前时间的分钟数,
H2:指定完成核算时间的小时数。
M2:指定完成核算时间的分钟数。
N:所有核酸检测点个数。
ID1:核酸点的ID值。
D1:核酸检测点距离张三的距离。
C1:核酸检测点当前检测的人数。
输出描述
N
I2 T2 M2
I3 T3 M3
N:满足要求的核酸检测点个数
I2:选择后的核酸检测点ID
T2:做完核酸花费的总时间(分钟)
M3:去该核算点花费的费用
用例
| 输入 | 10 30 14 50 3 1 10 19 2 8 20 3 21 3 |
| 输出 | 2 2 80 80 1 190 100 |
| 说明 | 无 |
题目解析
用例意思是:
张三在10:30出门,要在14:50之前做完核酸。
现在张三可选三个核酸检测点:
- 检测点1:距离张三10公里,10:30的时候有19个人排队
- 检测点2:距离张三8公里,10:30的时候有20个人排队
- 检测点3:距离张三21公里,10:30的时候有3个人排队
张三赶到检测点1,需要10*10 = 100元,10*10=100分钟,而在张三到达检测点时12:10,此时排队的人数是为:
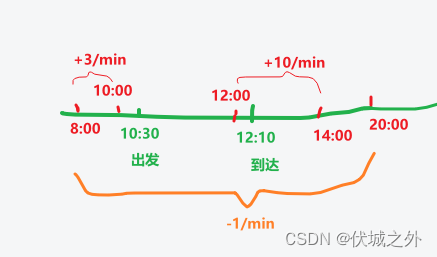
通过上图,我们可以看出:在10:30~12:00期间不会有人加入,只会有人离开,每分钟离开1人,因此到12:00时,最多离开 12*60 – (10*60+30) = 90人,而10:30时只有19人排队,因此到12:00时,检测点1只有0人排队。
然后12:00到12:10阶段,每分钟离开1人,增加10人,因此相当于每分钟净增9人,因此到12:10,即张三到达时,检测点共有:10 * 9 = 90人。
因此张三还需排90分钟,才能做完核酸。
因此张三到检测点1的代价是:路上100分钟,到达后等待90分钟,共需190分钟,花费100元。
同理,可得张三去其他检测点的代价。
然后,过滤掉花费时间超出限制的代价,剩下的按照花费时间、花费金额排序即可。
我们可以通过求区间交集的方式,来获取张三【出发时间,到达时间】 和 【8:00,10:00】以及【10:00, 12:00】,以及【12:00, 14:00】以及【14:00,20:00】的交集。
其中,
- 和 【8:00,10:00】的交集,每分钟净增2人
- 和 【10:00, 12:00】的交集,每分钟净减1人
- 和 【12:00, 14:00】的交集,每分钟净增9人
- 和 【14:00,20:00】的交集,每分钟净减1人
2023.1.17补充说明:
根据网友m0_71826536的提示,如果张三在8:00前就赶到了核酸监测点,但是8:00前是不给排队的,因此张三还要等待到8:00,因此张三花费的时间其实是:路上时间 + 等待时间 + 排队时间
2023.03.20补充说明
有同学考到这题后,按照上面逻辑写,得到通过率20%,我分析了一下原因,有可能是下面逻辑有问题:
张三在八点前赶到时,排在了初始人数的前面,即第一个进行核酸检测。
其实,根据题目用例来看,改成下面这个逻辑,也一样可行
张三在八点前赶到时,排在了初始人数的后面
下面代码补充了该场景,大家可以参照代码来看
2023.03.21 补充说明
之前题目描述不全,新增如下规则:
- 18点-20点每分钟增加20人。
- 其他时间每5分钟增加1人。
2023.04.06 补充说明
张三最迟做完核酸的时间点,不能早于8点,不能迟于20点
因为题目说:
每个核酸点工作时间都是8点到20点中间不休息,核酸点准时工作,早到晚到都不检测
Java修改了35行,JS修改了37行,Python修改了30行
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int h1 = sc.nextInt();
int m1 = sc.nextInt();
int h2 = sc.nextInt();
int m2 = sc.nextInt();
int n = sc.nextInt();
int[][] targets = new int[n][3];
for (int i = 0; i < n; i++) {
targets[i][0] = sc.nextInt();
targets[i][1] = sc.nextInt();
targets[i][2] = sc.nextInt();
}
getResult(h1, m1, h2, m2, targets);
}
/**
* @param h1 当前时间的小时数
* @param m1 当前时间的分钟数
* @param h2 指定完成核算时间的小时数
* @param m2 指定完成核算时间的分钟数
* @param targets 元素也是数组,元素数组含义为[核酸点的ID值, 核酸检测点距离张三的距离,核酸检测点当前检测的人数]
*/
public static void getResult(int h1, int m1, int h2, int m2, int[][] targets) {
int start = h1 * 60 + m1; // 张三出发的时间点
// int expect_end = h2 * 60 + m2; // 张三最迟做完核酸的时间点
int expect_end = Math.min(h2 * 60 + m2, 20 * 60); // 张三最迟做完核酸的时间点,不能迟于20点
double[][] times = {
{8 * 60, 10 * 60, 2}, // 8点~10点,每分钟增加2人
{10 * 60, 12 * 60, -0.8}, // 10点~12点,每分钟减少0.8人。(每五分钟新增1人,而每分钟减少1人,因此相当于每分钟减少0.8人)
{12 * 60, 14 * 60, 9}, // 12~14点,每分钟增加9人
{14 * 60, 18 * 60, -0.8}, // 14~18点,每分钟减少0.8人
{18 * 60, 20 * 60, 19}, // 18~20点,每分钟增加19人
};
int[][] ans =
Arrays.stream(targets)
.map(
target -> {
int id = target[0]; // 核酸点id
int dis = target[1]; // 核酸点和张三的距离
int wait = target[2]; // 核酸点在张三出发时已有的人数,每个人检测需要1分钟
int arrived = start + dis * 10; // 张三到达核酸点的时间
if (arrived < 8 * 60) {
arrived = 8 * 60;
// 张三在八点之前到达,排在初始人数后面
return new int[] {id, arrived - start + wait, dis * 10};
// 张三在八点之前到达,排在初始人数前面
// return new int[] {id, arrived - start, dis * 10}; // 此解法通过率20%
}
double s1 = start;
double e1 = arrived;
for (double[] time : times) {
double s2 = time[0];
double e2 = time[1];
double changePerMinutes = time[2];
double t = intersection(s1, e1, s2, e2);
if (t > 0) {
wait += t * changePerMinutes;
wait = Math.max(0, wait);
}
}
return new int[] {id, arrived - start + wait, dis * 10};
})
.filter(arr -> start + arr[1] <= expect_end)
.sorted((a, b) -> a[1] != b[1] ? a[1] - b[1] : a[2] != b[2] ? a[2] - b[2] : a[0] - b[0])
.toArray(int[][]::new);
System.out.println(ans.length);
for (int[] an : ans) {
System.out.println(an[0] + " " + an[1] + " " + an[2]);
}
}
public static double intersection(double s1, double e1, double s2, double e2) {
if (s1 <= s2 && e1 > s2) {
return Math.min(e1, e2) - s2;
}
if (s1 >= s2 && e2 > s1) {
return Math.min(e1, e2) - s1;
}
return 0;
}
}
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let h1, m1, h2, m2, n;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 3) {
[h1, m1] = lines[0].split(" ").map(Number);
[h2, m2] = lines[1].split(" ").map(Number);
n = lines[2] - 0;
}
if (n && lines.length === n + 3) {
const targets = lines.slice(3).map((line) => line.split(" ").map(Number));
getResult(h1, m1, h2, m2, targets);
lines.length = 0;
}
});
/**
*
* @param {*} h1 当前时间的小时数
* @param {*} m1 当前时间的分钟数
* @param {*} h2 指定完成核算时间的小时数
* @param {*} m2 指定完成核算时间的分钟数
* @param {*} targets [[核酸点的ID值, 核酸检测点距离张三的距离,核酸检测点当前检测的人数]]
*/
function getResult(h1, m1, h2, m2, targets) {
const start = h1 * 60 + m1; // 张三出发的时间点
// const expect_end = h2 * 60 + m2; // 张三最迟做完核酸的时间点
const expect_end = Math.min(h2 * 60 + m2, 20 * 60); // 张三最迟做完核酸的时间点,不能早于8点,不能迟于20点
const times = [
[8 * 60, 10 * 60, 2], // 8点~10点,每分钟增加2人
[10 * 60, 12 * 60, -0.8], // 10点~12点,每分钟减少0.8人
[12 * 60, 14 * 60, 9], // 12~14点,每分钟增加9人
[14 * 60, 18 * 60, -0.8], // 14点~18点,每分钟减少0.8人
[18 * 60, 20 * 60, 19], // 18~20点,每分钟新增19人
];
const ans = targets
.map((target) => {
let [id, dis, wait] = target; // [核酸点id, 核酸点和张三的距离, 核酸点在张三出发时已有的人数,每个人检测需要1分钟]
let arrived = start + dis * 10;
if (arrived < 8 * 60) {
arrived = 8 * 60;
// 张三在八点之前到达,排在初始人数后面
return [id, arrived - start + wait, dis * 10];
// 张三在八点之前到达,排在初始人数前面
// return [id, arrived - start, dis * 10]; // 此解法通过率20%
}
const s1 = start;
const e1 = arrived;
for (let [s2, e2, changePerMinutes] of times) {
const t = intersection(s1, e1, s2, e2);
if (t > 0) {
wait += t * changePerMinutes;
wait = Math.max(0, wait);
}
}
return [id, arrived - start + wait, dis * 10];
})
.filter((arr) => start + arr[1] <= expect_end)
.sort((a, b) =>
a[1] != b[1] ? a[1] - b[1] : a[2] != b[2] ? a[2] - b[2] : a[0] - b[0]
);
console.log(ans.length);
ans.forEach((an) => console.log(an.join(" ")));
}
function intersection(s1, e1, s2, e2) {
if (s1 <= s2 && e1 > s2) {
return Math.min(e1, e2) - s2;
}
if (s1 >= s2 && e2 > s1) {
return Math.min(e1, e2) - s1;
}
return 0;
}
Python算法源码
# 输入获取
h1, m1 = map(int, input().split())
h2, m2 = map(int, input().split())
n = int(input())
targets = [list(map(int, input().split())) for i in range(n)]
def intersection(s1, e1, s2, e2):
if s1 <= s2 < e1:
return min(e1, e2) - s2
if s2 <= s1 < e2:
return min(e1, e2) - s1
return 0
# 算法入口
def getResult(h1, m1, h2, m2, targets):
"""
:param h1: 当前时间的小时数
:param m1: 当前时间的分钟数
:param h2: 指定完成核算时间的小时数
:param m2: 指定完成核算时间的分钟数
:param targets: [[核酸点的ID值, 核酸检测点距离张三的距离,核酸检测点当前检测的人数]]
"""
start = h1 * 60 + m1
# expect_end = h2 * 60 + m2
expect_end = min(h2 * 60 + m2, 20 * 60) # 张三最迟做完核酸的时间点,不能早于8点,不能迟于20点
# 8点~10点,每分钟增加2人
# 10点~12点,每分钟减少0.8人
# 12~14点,每分钟增加9人
# 14~18点,每分钟减少0.8人
# 18~20点,每分钟增加19人
times = [[8 * 60, 10 * 60, 2],
[10 * 60, 12 * 60, -0.8],
[12 * 60, 14 * 60, 9],
[14 * 60, 18 * 60, -0.8],
[18 * 60, 20 * 60, 19]]
def mapFn(target):
id, dis, wait = target # [核酸点id, 核酸点和张三的距离, 核酸点在张三出发时已有的人数]
arrived = start + dis * 10
if arrived < 8 * 60:
arrived = 8 * 60
# 张三在八点之前到达,排在初始人数后面
return [id, arrived - start + wait, dis * 10]
# 张三在八点之前到达,排在初始人数前面
# return [id, arrived - start, dis * 10] # 此解法20%通过率
s1 = start
e1 = arrived
for s2, e2, changePerMinutes in times:
t = intersection(s1, e1, s2, e2)
if t > 0:
wait += t * changePerMinutes
wait = max(0, wait)
return [id, arrived - start + int(wait), dis * 10]
ans = list(filter(lambda x: start + x[1] <= expect_end, map(mapFn, targets)))
ans.sort(key=lambda x: (x[1], x[2], x[0]))
print(len(ans))
for an in ans:
print(" ".join(list(map(str, an))))
# 调用算法
getResult(h1, m1, h2, m2, targets)免责声明:
评论0