题目描述
如果一个数组中出现次数最多的元素出现大于等于K次,被称为 k-优雅数组 ,k也可以被称为优雅阈值。
例如,数组1,2,3,1、2,3,1,它是一个3-优雅数组,因为元素1出现次数大于等于3次,
数组[1, 2, 3, 1, 2]就不是一个3-优雅数组,因为其中出现次数最多的元素是1和2,只出现了2次。
给定一个数组A和k,请求出A有多少子数组是k-优雅子数组。
子数组是数组中一个或多个连续元素组成的数组。
例如,数组[1,2,3,4]包含10个子数组,分别是:
[1], [1,2], [1,2,3], [1,2,3,4], [2], [2,3], [2,3,4], [3], [3, 4], [4]。
输入描述
第一行输入两个数字,以空格隔开,含义是:A数组长度 k值
第二行输入A数组元素,以空格隔开
输出描述
输出A有多少子数组是k-优雅子数组
用例
| 输入 | 7 3 1 2 3 1 2 3 1 |
| 输出 | 1 |
| 说明 | 无 |
| 输入 | 7 2 1 2 3 1 2 3 1 |
| 输出 | 10 |
| 说明 | 无 |
题目解析
我的解题思路如下:
利用双指针(即一个双重for)找到所有子数组(有点暴力),外层 i 指针指向子数组左边界,内层 j 指针指向子数组右边界,然后统计子数组内部各数字出现个数,若有数字出现次数大于等于k,则该子数组符合要求,统计结果ans++。
上面算法逻辑中,找所有子数组的逻辑基本无法优化,但是统计每个子数组内部各数字出现次数的逻辑却可以优化。
我们可以基于动态规划前缀和的思想,对相同左边界的子数组,只统计初始子数组的内部元素个数,然后每当右边界变化,则基于上一个子数组的统计结果计算出新结果,例如:
自测用例:
7 2
1 2 3 1 2 3 1
左右指针移动图示

上面统计的都是以索引0元素开头的子数组情况。
当j指针移动到尾巴时,就可以i++,然后开始新一轮的统计,即统计以索引 i 元素开头的所有子数组中符合要求的个数,例如

这种前缀思想可以避免大量的重复统计工作。
同时,每轮统计我们只需要一个对象保存统计结果,一轮统计结束,则丢弃统计结果,不会占用太多内存。
2023.02.22 上面逻辑有机考同学反馈,通过率只有33%,后面用例不通过原因是超时。
其实上面逻辑超时的原因很容易发现,就是暴力枚举了所有子数组,因此必须优化子数组获取逻辑,和一位网友讨论后,发现上面逻辑有一个可以优化的点

那就是上图最找到符合要求的子串后,下一步的 i, j 指针运动逻辑,按照前面逻辑思路是:
- i 后移一位
- j 重新指向 i 新位置
即如下图所示,此时count也重新统计

但是真的有必要吗?
我们继续往下看,按照上面逻辑,我们必然会走到下图画红圈这一步,然后重新找到符合要求的子串

但是我们再回到下图第一轮时找到符合要求子串时的图示

有没有发现什么端倪呢?
其实,我们在第一轮结束时,不需要将 i,j 重头开始,而是可以直接:
- i++
即变为下图
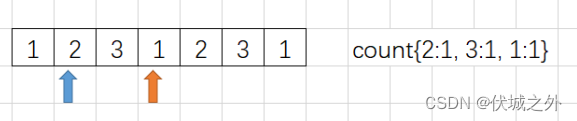
然后下一步j++,很快就会进入,前面第二轮经过多次指针运动后才能进入的状态

这个逻辑就非常节省时间了。
但是上面逻辑还是不够完善,比如大家看下面这个用例:
8 2
0 1 2 3 1 2 3 1
我按照上面新逻辑画图演示下双指针运动过程
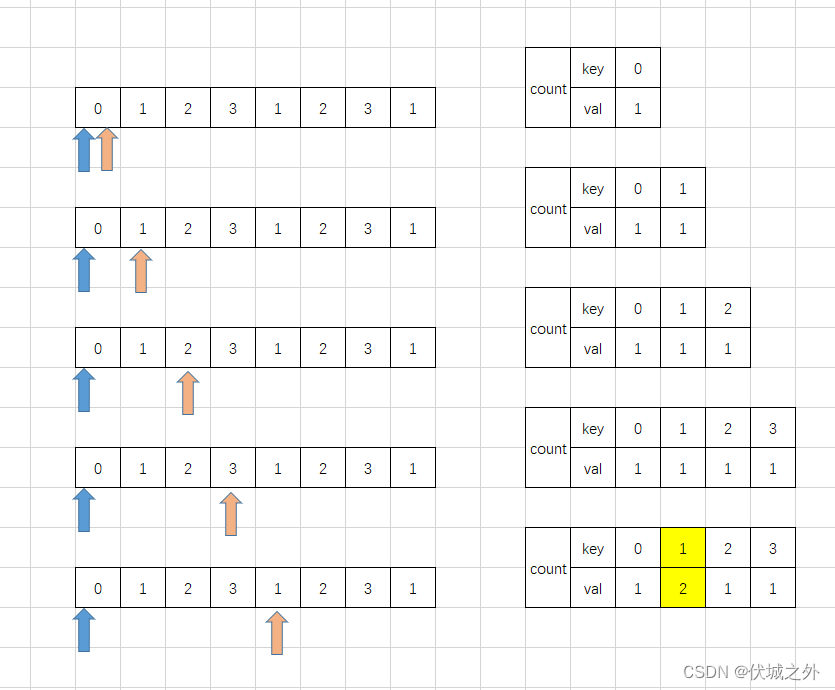
当走到最后一步时,我们就找到符合要求的子数组。
那么按照前面逻辑,下一步我们应该 i++(注意i++的时,对应的子数组就失去一个arr[i],因此对应count[arr[i]]数量要减少)

然后就又发现了符合要求的子数组,这一步在逻辑上没有问题,但是在代码实现上可能会发生问题,比如看下面伪代码:
l = 0 // 左指针
r = 0 // 右指针
// n是数组arr长度
while(l < n && r < n) {
c = arr[r] // r指针指向的数组元素就是将要加入的左右指针内部的元素
// count用于统计左右指针内部(子数组)c字符出现的次数
count[c]++
// k阈值
if(count[c] >= k) {
ans += n - r // 发现符合要求的子数组后,可以拓展出n-r个符合要求的子数组
count[arr[l]]-- // 左指针右移一格,但是右移前要减去左指针指向字符的统计次数
l++
}
r++ // 右指针移动
}上面代码大家有发现问题吗?
问题出在左指针L右移一格后,右指针R也右移了一格,即如下图所示
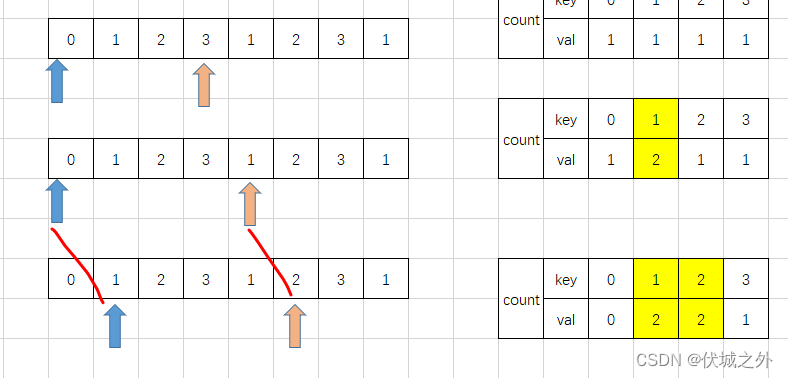
此时其实就遗漏部分符合要求的子数组情况。大家可以对照前面正确运动过程想一下。
那么该怎么改呢?
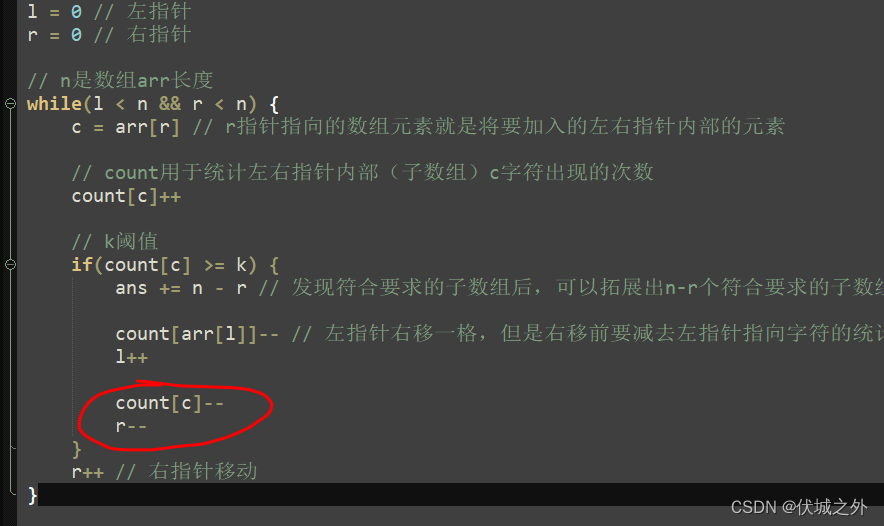
即在R指针右移前,做一次左移即可。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, k;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
[n, k] = lines[0].split(" ").map(Number);
const arr = lines[1].split(" ").map(Number);
console.log(getResult(arr, n, k));
lines.length = 0;
}
});
function getResult(arr, n, k) {
let ans = 0;
let l = 0;
let r = 0;
const count = {};
while (l < n && r < n) {
const c = arr[r];
count[c] ? count[c]++ : (count[c] = 1);
if (count[c] >= k) {
ans += n - r;
count[arr[l]]--;
l++;
count[c]--;
r--;
}
r++;
}
return ans;
}
Java算法源码
import java.util.HashMap;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int k = sc.nextInt();
Integer[] arr = new Integer[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
System.out.println(getResult(arr, n, k));
}
public static Integer getResult(Integer[] arr, Integer n, Integer k) {
int ans = 0;
int l = 0;
int r = 0;
HashMap<Integer, Integer> count = new HashMap<>();
while (l < n && r < n) {
Integer c = arr[r];
count.put(c, count.getOrDefault(c, 0) + 1);
if (count.get(c) >= k) {
ans += n - r;
count.put(arr[l], count.get(arr[l]) - 1);
l++;
count.put(c, count.get(c) - 1);
r--;
}
r++;
}
return ans;
}
}
Python算法源码
# 输入获取
n, k = map(int, input().split())
arr = list(map(int, input().split()))
# 算法入口
def getResult(arr, n, k):
ans = 0
l = 0
r = 0
count = {}
while l < n and r < n:
c = arr[r]
if count.get(c) is None:
count[c] = 0
count[c] += 1
if count[c] >= k:
ans += n - r
count[arr[l]] -= 1
l += 1
count[c] -= 1
r -= 1
r += 1
return ans
# 算法调用
print(getResult(arr, n, k))
免责声明:
评论0