题目描述
有一个二维的天线矩阵,每根天线可以向其他天线发射信号,也能接收其他天线的信号,为了简化起见,我们约定每根天线只能向东和向南发射信号,换言之,每根天线只能接收东向或南向的信号。
每根天线有自己的高度anth,每根天线的高度存储在一个二维数组中,各个天线的位置用[r, c]表示,r代表天线的行位置(从0开始编号),c代表天线的列位置(从0开始编号)。
在某一方向(东向或南向),某根天线可以收到多根其他天线的信号(也可能收不到任何其他天线的信号),对任一天线X和天线Y,天线X能接收到天线Y的条件是:
- 天线X在天线Y的东边或南边
- 天线X和天线Y之间的其他天线的高度都低于天线X和天线Y,或天线X和天线Y之间无其他天线,即无遮挡。
如下图示意:
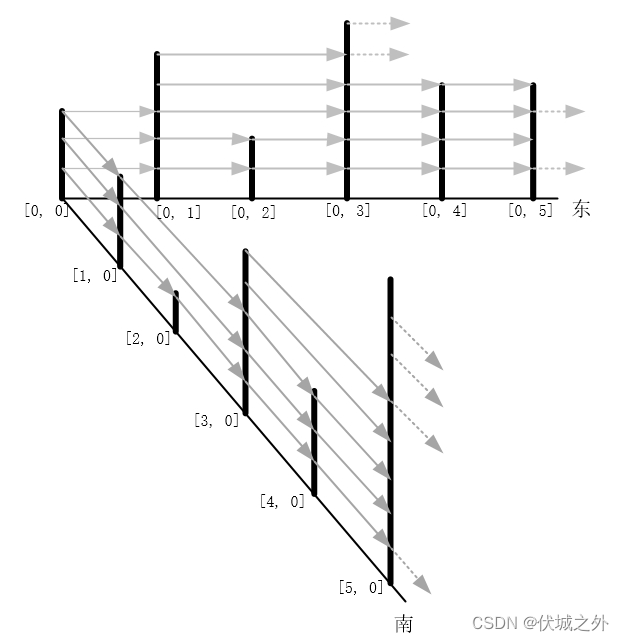
在天线矩阵的第0行上:
- 天线[0, 0]接收不到任何其他天线的信号,
- 天线[0, 1]可以接收到天线[0, 0]的信号,
- 天线[0, 2]可以接收到天线[0, 1]的信号,
- 天线[0, 3]可以接收到天线[0, 1]和天线[0, 2]的信号,
- 天线[0, 4]可以接收到天线[0, 3]的信号,
- 天线[0, 5]可以接收到天线[0, 4]的信号;
在天线的第0列上:
- 天线[0, 0]接收不到任何其他天线的信号,
- 天线[1, 0]可以接收到天线[0, 0]的信号,
- 天线[2, 0]可以接收到天线[1, 0]的信号,
- 天线[3, 0]可以接收到天线[1, 0]和天线[2, 0]的信号,
- 天线[4, 0]可以接收到天线[3, 0]的信号,
- 天线[5, 0]可以接收到天线[3, 0]和天线[4, 0]的信号;
给一个m行n列的矩阵(二维数组),矩阵存储各根天线的高度,求出每根天线可以接收到多少根其他天线的信号,结果输出到m行n列的矩阵(二维矩阵)中。
输入描述
输入为1个m行n列的矩阵(二维矩阵)anth[m][n],矩阵存储各根天线的高度,高度值anth[r]][c]为大于0的整数。
第一行为输入矩阵的行数和列数,如:
m n
第二行为输入矩阵的元素值,按行输入,如:
anth[0][0] anth[0][1] … anth[0][n-1] anth[1][0] anth[1][1] … anth[1][n-1] … anth[m-1][0] … anth[m-1][n-1]
输出描述
输出一个m行n列的矩阵(二维数组)ret[m][n],矩阵存储每根天线能收到多少根其他天线的信号,根数为ret[r][c]。
第一行为输出矩阵的行数和列数,如:
m n
第二行为输出矩阵的元素值,按行输出,如:
ret[0][0] ret[0][1] … ret[0][n-1] ret[1][0] ret[1][1] … ret[1][n-1] … ret[m-1][0] … ret[m-1][n-1]
备注
- 1 ≤ m ≤ 500
- 1 ≤ n ≤ 500
- 0 < anth[r][c] < 10^5
用例
| 输入 | 1 6 2 4 1 5 3 3 |
| 输出 | 1 6 0 1 1 2 1 1 |
| 说明 |
输入为1行6列的天线矩阵的高度值 [2 4 1 5 3 3] 输出为1行6列的结果矩阵 [0 1 1 2 1 1] |
| 输入 | 2 6 2 5 4 3 2 8 9 7 5 10 10 3 |
| 输出 | 2 6 0 1 1 1 1 4 1 2 2 4 2 2 |
| 说明 |
输入为2行6列的天线矩阵高度值 [2 5 4 3 2 8] [9 7 5 10 10 3] 输出为2行6列的结果矩阵 [0 1 1 1 1 4] [1 2 2 4 2 2] |
题目解析
首先,本题我们需要从输入的一维数组中解析出二维天线矩阵,JS的实现略微麻烦,具体逻辑请看源码。
下面我们以用例1为例子,来解析本题,如下图是用例1的二维天线矩阵anth
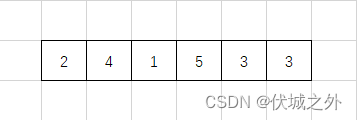
我们从anth[0][0]开始发射,本题说了,天线信号发射只能向东或者向南发射,即如下图所示
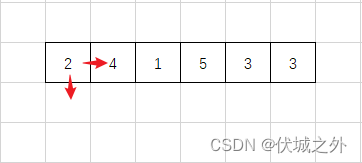
由于用例1只有一层,因此只需要考虑向东发射信号。
而东边的天线是否能收到信号,也有前提条件,即“发射天线”与“接收天线”之间的天线的高度都低于“发射天线”与“接收天线”,或者“发射天线”与“接收天线”之间没有其他天线
因此,上面用例1中anth[0][0]可以发射到anth[0][1],因为它们之间没有其他天线
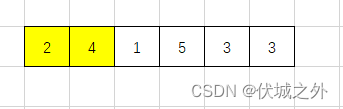
但是anth[0][0]不能发射到anth[0][2],因为它们之间的天线大于等于了它们
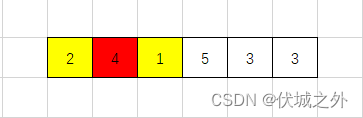
其实这一步,不需要走到anth[0][2],因为anth[0][1] >= anth[0][0],因此anth[0][0]必然会被anth[0][1]遮挡,导致无法继续向东发射。
因此,对于anth[0][0]作为发射点的所有情况已经讨论完了,它只有一个接收点,那就是anth[0][1]。
接下来继续讨论anth[0][1]作为发射点
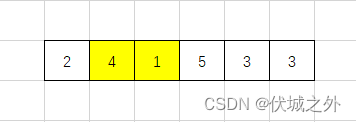
首先,相邻的anth[0][2]肯定能接收到信号。
并且由于anth[0][2]小于anth[0][1],因此无法完全将anth[0][1]发射的信号遮挡,
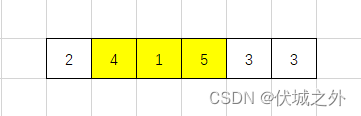
因此anth[0][3]可以接收到anth[0][1]的信号?
注意:这里我打了一个问号,因为题目要求,如果“发射天线”和“接收天线”之间有其他天线,那么其他天线的高度必须低于“发射天线”和“接收天线”。
上面打问号的原因是:我们只判断了中间天线 anth[0][2] < anth[0][1] 发射天线,并没有判断中间天线 anth[0][2] 也小于 anth[0][3] 接收天线。
- 而,这里中间天线 anth[0][2] 确实是小于 anth[0][3] 接收天线的,因此anth[0][3]可以接收到anth[0][1]的信号。
如果,我们采用双重for,外层遍历发射天线,内层遍历接收天线,则还需一个for遍历求得发射天线和接收天线之间的:所有中间天线中最高的高度h,如果这个高度h 大于等于发射天线,或者接收天线,则发射天线和接收天线之间无法进行通信。
这其实已经是三重for了,再加上每个天线都会接收来自东向和南向这两个方向的信号,因此需要进行两次三重for。
这里的优化,我们可以利用单调递减栈。
首先定义一个单调递减栈stack,然后开始遍历天线anth[i][j](比如先处理东向,即按行从左到右遍历):
1、如果stack为空,则直接将天线anth[i][j]加入stack
2、如果stack不为空,则获取栈顶天线top
2.1、如果anth[i][j] > top,则将stack栈顶的top弹出,然后anth[i][j]对应的ret[i][j]++,表示anth[i][j]天线新增接收一个信号,而由于stack栈是递减栈,因此anth[i][j]还可以继续接收新栈顶天线的信号
2.2、如果anth[i][j] == top,则将stack栈顶的top弹出,然后anth[i][j]新增接收一个信号,ret[i][j]++。(注意,由于stack是严格递减栈,因此如果栈顶元素和anth[i][j]等高,则必然只有一个,且stack弹栈后的新栈顶必然大于anth[i][j],此时其实可以直接结束)
2.3、如果anth[i][j] < top,则表示anth[i][j]已经无法接收到top之前的信号了,因为已经被top完全阻挡了。因此anth[i][j]只能栈顶天线的信号,ret[i][j]++,而无法继续接收前面天线的信号。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
const [m, n] = lines[0].split(" ").map(Number);
const arr = lines[1].split(" ").map(Number);
console.log(getResult(arr, m, n));
lines.length = 0;
}
});
function getResult(arr, m, n) {
const anth = new Array(m).fill(0).map(() => new Array(n));
for (let i = 0; i < m * n; i++) {
const r = Math.floor(i / n);
const c = i % n;
anth[r][c] = arr[i];
}
const ret = new Array(m).fill(0).map(() => new Array(n).fill(0));
// 先处理水平方向,即先进行每行的东向发射处理
for (let i = 0; i < m; i++) {
const stack = [];
for (let j = 0; j < n; j++) {
// 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while (stack.length && anth[i][j] > stack.at(-1)) {
ret[i][j]++;
stack.pop();
}
// 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然 >= anth[i][j]
if (stack.length) {
// 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if (anth[i][j] == stack.at(-1)) {
ret[i][j]++;
stack.pop(); // 维护严格递减栈
}
// 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else {
ret[i][j]++;
}
}
stack.push(anth[i][j]);
}
}
// 再处理垂直方向,即每列的南向发射处理,和上面同理
for (let j = 0; j < n; j++) {
const stack = [];
for (let i = 0; i < m; i++) {
// 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while (stack.length && anth[i][j] > stack.at(-1)) {
ret[i][j]++;
stack.pop();
}
// 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然 >= anth[i][j]
if (stack.length) {
// 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if (anth[i][j] == stack.at(-1)) {
ret[i][j]++;
stack.pop(); // 维护严格递减栈
}
// 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else {
ret[i][j]++;
}
}
stack.push(anth[i][j]);
}
}
return `${m} ${n}n${ret.toString().split(",").join(" ")}`;
}
提取公共代码,优化代码结构
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
const [m, n] = lines[0].split(" ").map(Number);
const arr = lines[1].split(" ").map(Number);
console.log(getResult(arr, m, n));
lines.length = 0;
}
});
function getResult(arr, m, n) {
const anth = new Array(m).fill(0).map(() => new Array(n));
for (let i = 0; i < m * n; i++) {
const r = Math.floor(i / n);
const c = i % n;
anth[r][c] = arr[i];
}
const ret = new Array(m).fill(0).map(() => new Array(n).fill(0));
// 先处理水平方向,即先进行每行的东向发射处理
for (let i = 0; i < m; i++) {
const stack = [];
for (let j = 0; j < n; j++) {
common(stack, anth, ret, i, j);
}
}
// 再处理垂直方向,即每列的南向发射处理,和上面同理
for (let j = 0; j < n; j++) {
const stack = [];
for (let i = 0; i < m; i++) {
common(stack, anth, ret, i, j);
}
}
return `${m} ${n}n${ret.toString().split(",").join(" ")}`;
}
function common(stack, anth, ret, i, j) {
// 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while (stack.length && anth[i][j] > stack.at(-1)) {
ret[i][j]++;
stack.pop();
}
// 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然 >= anth[i][j]
if (stack.length) {
// 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if (anth[i][j] == stack.at(-1)) {
ret[i][j]++;
stack.pop(); // 维护严格递减栈
}
// 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else {
ret[i][j]++;
}
}
stack.push(anth[i][j]);
}
Java算法源码
import java.util.LinkedList;
import java.util.Scanner;
import java.util.StringJoiner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int n = sc.nextInt();
int[][] anth = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
anth[i][j] = sc.nextInt();
}
}
System.out.println(getResult(anth, m, n));
}
public static String getResult(int[][] anth, int m, int n) {
int[][] ret = new int[m][n];
// 先处理南向发射信号
for (int j = 0; j < n; j++) {
LinkedList<Integer> stack = new LinkedList<>();
for (int i = 0; i < m; i++) {
// 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while (stack.size() > 0 && anth[i][j] > stack.getLast()) {
ret[i][j] += 1;
stack.removeLast();
}
// 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然
if (stack.size() > 0) {
// 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,
// 比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if (anth[i][j] == stack.getLast()) {
ret[i][j] += 1;
stack.removeLast(); // 维护严格递减栈
}
// 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,
// 比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else {
ret[i][j] += 1;
}
}
stack.add(anth[i][j]);
}
}
StringJoiner sj = new StringJoiner(" ");
// 再处理东向发射信号,和上面同理
for (int i = 0; i < m; i++) {
LinkedList<Integer> stack = new LinkedList<>();
for (int j = 0; j < n; j++) {
// 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while (stack.size() > 0 && anth[i][j] > stack.getLast()) {
ret[i][j] += 1;
stack.removeLast();
}
// 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然
if (stack.size() > 0) {
// 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,
// 比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if (anth[i][j] == stack.getLast()) {
ret[i][j] += 1;
stack.removeLast(); // 维护严格递减栈
}
// 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,
// 比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else {
ret[i][j] += 1;
}
}
stack.add(anth[i][j]);
sj.add(ret[i][j] + "");
}
}
return m + " " + n + "n" + sj.toString();
}
}
提取公共代码,优化代码结构
import java.util.LinkedList;
import java.util.Scanner;
import java.util.StringJoiner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int n = sc.nextInt();
int[][] anth = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
anth[i][j] = sc.nextInt();
}
}
System.out.println(getResult(anth, m, n));
}
public static String getResult(int[][] anth, int m, int n) {
int[][] ret = new int[m][n];
// 先处理南向发射信号
for (int j = 0; j < n; j++) {
LinkedList<Integer> stack = new LinkedList<>();
for (int i = 0; i < m; i++) {
common(stack, anth, ret, i, j);
}
}
StringJoiner sj = new StringJoiner(" ");
// 再处理东向发射信号,和上面同理
for (int i = 0; i < m; i++) {
LinkedList<Integer> stack = new LinkedList<>();
for (int j = 0; j < n; j++) {
common(stack, anth, ret, i, j);
sj.add(ret[i][j] + "");
}
}
return m + " " + n + "n" + sj.toString();
}
public static void common(LinkedList<Integer> stack, int[][] anth, int[][] ret, int i, int j) {
// 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while (stack.size() > 0 && anth[i][j] > stack.getLast()) {
ret[i][j] += 1;
stack.removeLast();
}
// 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然
if (stack.size() > 0) {
// 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,
// 比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if (anth[i][j] == stack.getLast()) {
ret[i][j] += 1;
stack.removeLast(); // 维护严格递减栈
}
// 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,
// 比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else {
ret[i][j] += 1;
}
}
stack.add(anth[i][j]);
}
}
Python算法源码
# 输入获取
m, n = map(int, input().split())
arr = list(map(int, input().split()))
# 算法源码
def getResult(m, n, arr):
anth = [[0 for j in range(n)] for i in range(m)]
for i in range(m * n):
r = int(i / n)
c = i % n
anth[r][c] = arr[i]
ret = [[0 for j in range(n)] for i in range(m)]
# 先处理东向发射信号
for i in range(m):
stack = []
for j in range(n):
# 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while len(stack) > 0 and anth[i][j] > stack[-1]:
ret[i][j] += 1
stack.pop()
# 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然
if len(stack) > 0:
# 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if anth[i][j] == stack[-1]:
ret[i][j] += 1
stack.pop() # 维护严格递减栈
# 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else:
ret[i][j] += 1
stack.append(anth[i][j])
# 再处理南向发射信号
for j in range(n):
stack = []
for i in range(m):
# 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while len(stack) > 0 and anth[i][j] > stack[-1]:
ret[i][j] += 1
stack.pop()
# 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然
if len(stack) > 0:
# 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if anth[i][j] == stack[-1]:
ret[i][j] += 1
stack.pop() # 维护严格递减栈
# 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else:
ret[i][j] += 1
stack.append(anth[i][j])
res = " ".join([" ".join(map(str, i)) for i in ret])
print(f'{m} {n}n{res}')
# 算法调用
getResult(m, n, arr)
提取公共代码,优化代码结构
# 输入获取
m, n = map(int, input().split())
arr = list(map(int, input().split()))
def common(stack, anth, ret, i, j):
# 如果栈顶天线比anth[i][j],则anth[i][j]必然能接收到栈顶天线的信号,并且还能继续接收栈顶前面一个天线的信号(递减栈,栈顶前面天线高度必然大于栈顶天线高度)
while len(stack) > 0 and anth[i][j] > stack[-1]:
ret[i][j] += 1
stack.pop()
# 走到此步,如果stack还有值,那么由于是递减栈,因此此时栈顶天线高度必然
if len(stack) > 0:
# 如果栈顶天线高度 == anth[i][j],那么此时anth[i][j]可以接收栈顶天线的信号,比如5 3 2 3,最后一个3可以接收到前面等高3的信号,但是无法继续接收前面5的信号,因此这里anth[i][j]结束处理
if anth[i][j] == stack[-1]:
ret[i][j] += 1
stack.pop() # 维护严格递减栈
# 此情况必然是:anth[i][j] < stack.at(-1),那么此时anth[i][j]可以接收栈顶天线的信号,比如6 5 2 3,最后一个3可以接收到前面5的信号,但是无法继续接收更前面6的信号,因此这里anth[i][j]结束处理
else:
ret[i][j] += 1
stack.append(anth[i][j])
# 算法源码
def getResult(m, n, arr):
anth = [[0 for j in range(n)] for i in range(m)]
for i in range(m * n):
r = int(i / n)
c = i % n
anth[r][c] = arr[i]
ret = [[0 for j in range(n)] for i in range(m)]
# 先处理东向发射信号
for i in range(m):
stack = []
for j in range(n):
common(stack, anth, ret, i, j)
# 再处理南向发射信号
for j in range(n):
stack = []
for i in range(m):
common(stack, anth, ret, i, j)
res = " ".join([" ".join(map(str, i)) for i in ret])
print(f'{m} {n}n{res}')
# 算法调用
getResult(m, n, arr)
免责声明:
评论0