题目描述
从一个长度为N的正数数组numbers中找出长度至少为L且几何平均值最大子数组,并输出其位置和大小。(K个数的几何平均值为K个数的乘积的K次方根)
若有多个子数组的几何平均值均为最大值,则输出长度最小的子数组。
若有多个长度相同的子数组的几何平均值均为最大值,则输出最前面的子数组。
输入描述
第一行输入为N、L
- N表示numbers的大小(1 ≤ N ≤ 100000)
- L表示子数组的最小长度(1 ≤ L ≤ N)
之后N行表示numbers中的N个数,每个一行(10^-9 ≤ numbers[i] ≤ 10^9)
输出描述
输出子数组的位置(从0开始计数)和大小,中间用一个空格隔开。
备注
用例保证除几何平均值为最大值的子数组外,其他子数组的几何平均值至少比最大值小10^-10倍
用例
| 输入 | 3 2 2 2 3 |
| 输出 | 1 2 |
| 说明 | 长度至少为2的子数组共三个,分别是{2,2}、{2,3}、{2,2,3},其中{2,3}的几何平均值最大,故输出其位置1和长度2 |
| 输入 | 10 2 0.2 0.1 0.2 0.2 0.2 0.1 0.2 0.2 0.2 0.2 |
| 输出 | 2 2 |
| 说明 | 有多个长度至少为2的子数组的几何平均值为0.2,其中长度最短的为2,也有多个,长度为2且几何平均值为0.2的子数组最前面的那个为从第二个数开始的两个0.2组成的子数组 |
二分+前缀积解法(不适用于本题,可以不看,具体原因看下一个解法)
题目解析
本题其实就是
的变种题。但是本题更难。
建议大家先把leetcode 644 这题做会了,再来看本题。
本题和leetcode 644的区别在于,leetcode 644求解的长度大于等于k的 最大算术平均值 的连续子序列,而本题求解的是 长度大于等于k的 最大几何平均值 的连续子序列。
一个数组的nums = [a1, a2, a3, …, aN]的
- 算术平均值 = (a1 + a2 + a3 + … + aN) / N
- 几何平均值 = N √(a1 * a2 * a3 * …. * aN)
因此,在求解 长度大于等于k 的子序列时,我们不能在沿用leetcode 644的解法,leetcode 644解法如下
首先,求出 0~i 子序列的和 sum
然后,求出 0~0 到 0~i-k 中所有子序列的最小和 min_pre_sum
最后,sum – min_pre_sum >= 0的话,说明midVal可能取小了
本题需要换成除法
首先,求出 0~i 子序列的所有元素乘积 fact
然后,求出 0~0 到 0~i-k 中所有子序列的最小乘积 min_pre_fact
最后,fact / min_pre_fact >= 1的话,说明midVal可能取小了
原理如下:有一个数组nums = [a1, a2, a3, …, aN],假设其几何平均值为avg,则有等式如下:
N √ (a1 * a2 * a3 * … * aN) == avg
再转换一下,如下:
a1 * a2 * a3 * … * aN == avg ^ N
再转换一下,如下:
(a1 / avg) * (a2 / avg) * (a3 / avg) * … * (aN / avg) == 1
如果avg取大了,则 (a1 / avg) * (a2 / avg) * (a3 / avg) * … * (aN / avg) < 1
如果avg取小了,则 (a1 / avg) * (a2 / avg) * (a3 / avg) * … * (aN / avg) > 1
另外,本题需要输出最大几何平均值对应的子数组的起始位置和长度,这个很简单,只需要记录每次被挖去的最小平均值子数组的结尾索引即可,根据结尾索引min_pre_fact_end,即可得出最大平均值数组的起始索引和长度,计算公式如下
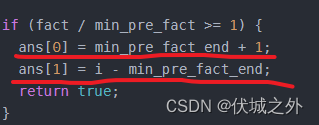
2023.04.09 根据网友指正,本题之前的解法没有考虑:存在多个最大几何平均值的子数组的情况,比如用例2,就有多个最大几何平均值,下面用JS通过暴力解法,求出所有子数组的几何平均值
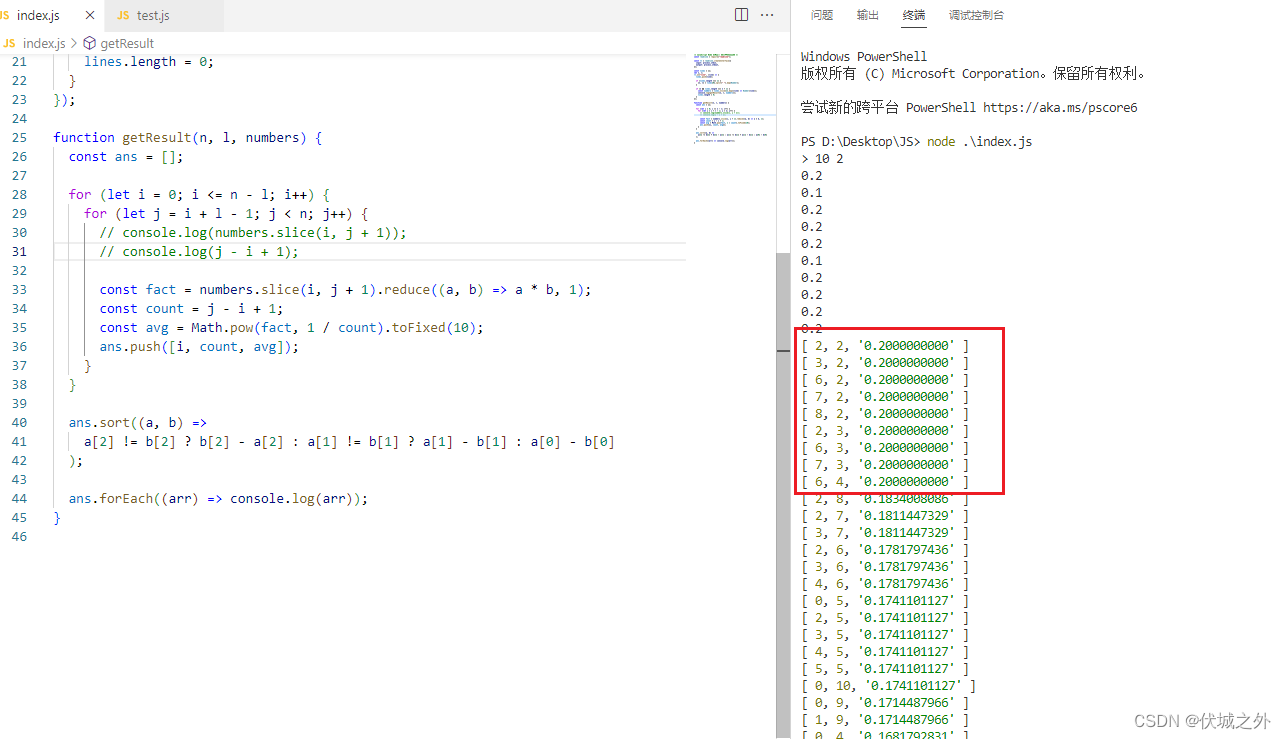
如上图所示,最大几何平均值为0.2,而几何平均值到达0.2的子数组有多个,
比如 [2, 2, '0.200000000000'] 的含义就是:起点索引2,长度2,的子数组的几何平均值就是0.2
因此,基于上面算法,当我们可以保存最后一轮二分求得的avg对应的:所有子数组的起点和长度(保存进ans),然后进行排序:先按照长度(较短者排前面),再按照起点(靠前者排在前面)、
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, l;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
[n, l] = lines[0].split(" ").map(Number);
}
if (n && lines.length === n + 1) {
const numbers = lines.slice(1).map((line) => Number(line));
console.log(getResult(n, l, numbers));
lines.length = 0;
}
});
function getResult(n, l, numbers) {
const sorted_numbers = numbers.slice().sort((a, b) => a - b);
let minAvg = sorted_numbers.at(0);
let maxAvg = sorted_numbers.at(-1);
// const diff = maxAvg / Math.pow(10, 10);
let ans = [];
// 其他子数组的几何平均值至少比最大值小10^-10倍
while (maxAvg - minAvg >= maxAvg / Math.pow(10, 10)) {
// 不保留历史avg对应的ans,只保留最后一个avg,即最大avg的ans
ans = [];
let midAvg = (minAvg + maxAvg) / 2;
if (check(n, l, numbers, midAvg, ans)) {
minAvg = midAvg;
} else {
maxAvg = midAvg;
}
}
// 若有多个子数组的几何平均值均为最大值,则输出长度最小的子数组。
// 若有多个长度相同的子数组的几何平均值均为最大值,则输出最前面的子数组。
ans.sort((a, b) => (a[1] != b[1] ? a[1] - b[1] : a[0] - b[0]));
return ans[0].join(" ");
}
function check(n, l, numbers, avg, ans) {
// 该flag为True表示avg取小了,为False表示avg取大了,默认为False
let flag = false;
let fact = 1;
for (let i = 0; i < l; i++) {
fact *= numbers[i] / avg;
}
if (fact >= 1) {
flag = true;
// ans的元素含义:[目标子数组起始位置,目标子数组长度]
ans.push([0, l]);
}
let pre_fact = 1;
let min_pre_fact = Infinity;
let min_pre_fact_end = 0;
for (let i = l; i < n; i++) {
fact *= numbers[i] / avg; // 对应0~i区间
pre_fact *= numbers[i - l] / avg; // 对应0~i-l区间
if (pre_fact < min_pre_fact) {
min_pre_fact = pre_fact; // 对应0~i-l区间内 几何平均值最小的子数列
min_pre_fact_end = i - l;
}
if (fact / min_pre_fact >= 1) {
flag = true;
// ans的元素含义:[目标子数组起始位置,目标子数组长度]
ans.push([min_pre_fact_end + 1, i - min_pre_fact_end]);
}
}
return flag;
}
Java算法源码
import java.util.ArrayList;
import java.util.Objects;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int l = sc.nextInt();
double[] numbers = new double[n];
for (int i = 0; i < n; i++) {
numbers[i] = sc.nextDouble();
}
System.out.println(getResult(n, l, numbers));
}
public static String getResult(int n, int l, double[] numbers) {
double minAvg = Integer.MAX_VALUE;
double maxAvg = Integer.MIN_VALUE;
for (double num : numbers) {
minAvg = Math.min(num, minAvg);
maxAvg = Math.max(num, maxAvg);
}
// double diff = maxAvg / Math.pow(10, 10);
ArrayList<Integer[]> ans = new ArrayList<>();
// 其他子数组的几何平均值至少比最大值小10^-10倍
while (maxAvg - minAvg >= maxAvg / Math.pow(10, 10)) {
// 不保留历史avg对应的ans,只保留最后一个avg,即最大avg的ans
ans = new ArrayList<>();
double midAvg = (minAvg + maxAvg) / 2;
if (check(n, l, numbers, midAvg, ans)) {
minAvg = midAvg;
} else {
maxAvg = midAvg;
}
}
// 若有多个子数组的几何平均值均为最大值,则输出长度最小的子数组。
// 若有多个长度相同的子数组的几何平均值均为最大值,则输出最前面的子数组。
ans.sort((a, b) -> !Objects.equals(a[1], b[1]) ? a[1] - b[1] : a[0] - b[0]);
Integer[] tmp = ans.get(0);
return tmp[0] + " " + tmp[1];
}
public static boolean check(
int n, int l, double[] numbers, double avg, ArrayList<Integer[]> ans) {
// 该flag为True表示avg取小了,为False表示avg取大了,默认为False
boolean flag = false;
double fact = 1;
for (int i = 0; i < l; i++) {
fact *= numbers[i] / avg;
}
if (fact >= 1) {
flag = true;
// ans的元素含义:[目标子数组起始位置,目标子数组长度]
ans.add(new Integer[] {0, l});
}
double pre_fact = 1;
double min_pre_fact = Integer.MAX_VALUE;
int min_pre_fact_end = 0;
for (int i = l; i < n; i++) {
fact *= numbers[i] / avg; // 对应0~i区间
pre_fact *= numbers[i - l] / avg; // 对应0~i-l区间
if (pre_fact < min_pre_fact) {
min_pre_fact = pre_fact; // 对应0~i-l区间内 几何平均值最小的子数列
min_pre_fact_end = i - l;
}
if (fact / min_pre_fact >= 1) {
flag = true;
// ans的元素含义:[目标子数组起始位置,目标子数组长度]
ans.add(new Integer[] {min_pre_fact_end + 1, i - min_pre_fact_end});
}
}
return flag;
}
}
Python算法源码
import sys
# 输入获取
n, l = map(int, input().split())
numbers = [float(input()) for i in range(n)]
# 算法入口
def getResult(n, l, numbers):
minAvg = min(numbers)
maxAvg = max(numbers)
# diff = maxAvg / 10 ** 10
ans = []
# 其他子数组的几何平均值至少比最大值小10^-10倍
while maxAvg - minAvg >= maxAvg / 10 ** 10:
# 不保留历史avg对应的ans,只保留最后一个avg,即最大avg的ans
ans = []
midAvg = (minAvg + maxAvg) / 2
if check(n, l, numbers, midAvg, ans):
minAvg = midAvg
else:
maxAvg = midAvg
# 若有多个子数组的几何平均值均为最大值,则输出长度最小的子数组。
# 若有多个长度相同的子数组的几何平均值均为最大值,则输出最前面的子数组。
ans.sort(key=lambda x: (x[1], x[0]))
return " ".join(map(str, ans[0]))
def check(n, l, numbers, avg, ans):
# 该flag为True表示avg取小了,为False表示avg取大了,默认为False
flag = False
fact = 1
for i in range(l):
fact *= numbers[i] / avg
if fact >= 1:
flag = True
# ans的元素含义:[目标子数组起始位置,目标子数组长度]
ans.append([0, l])
pre_fact = 1
min_pre_fact = sys.maxsize
min_pre_fact_end = 0
for i in range(l, n):
fact *= numbers[i] / avg # 对应0~i区间
pre_fact *= numbers[i - l] / avg # 对应0~i-l区间
if pre_fact < min_pre_fact:
min_pre_fact = pre_fact # 对应0~i-l区间内 几何平均值最小的子数列
min_pre_fact_end = i - l
if fact / min_pre_fact >= 1:
flag = True
# ans的元素含义:[目标子数组起始位置,目标子数组长度]
ans.append([min_pre_fact_end + 1, i - min_pre_fact_end])
return flag
# 算法调用
print(getResult(n, l, numbers))前缀积解法
题目解析
前面二分+前缀积的解法存在问题,比如下面用例:
7 4
0.5
0.5
2
2
2
0.5
8
这题大家可以用暴力解法,求出所有长度大于等于4的子数组,然后求解每个子数组的几何平均值,如下图是基于JS的暴力求解结果:
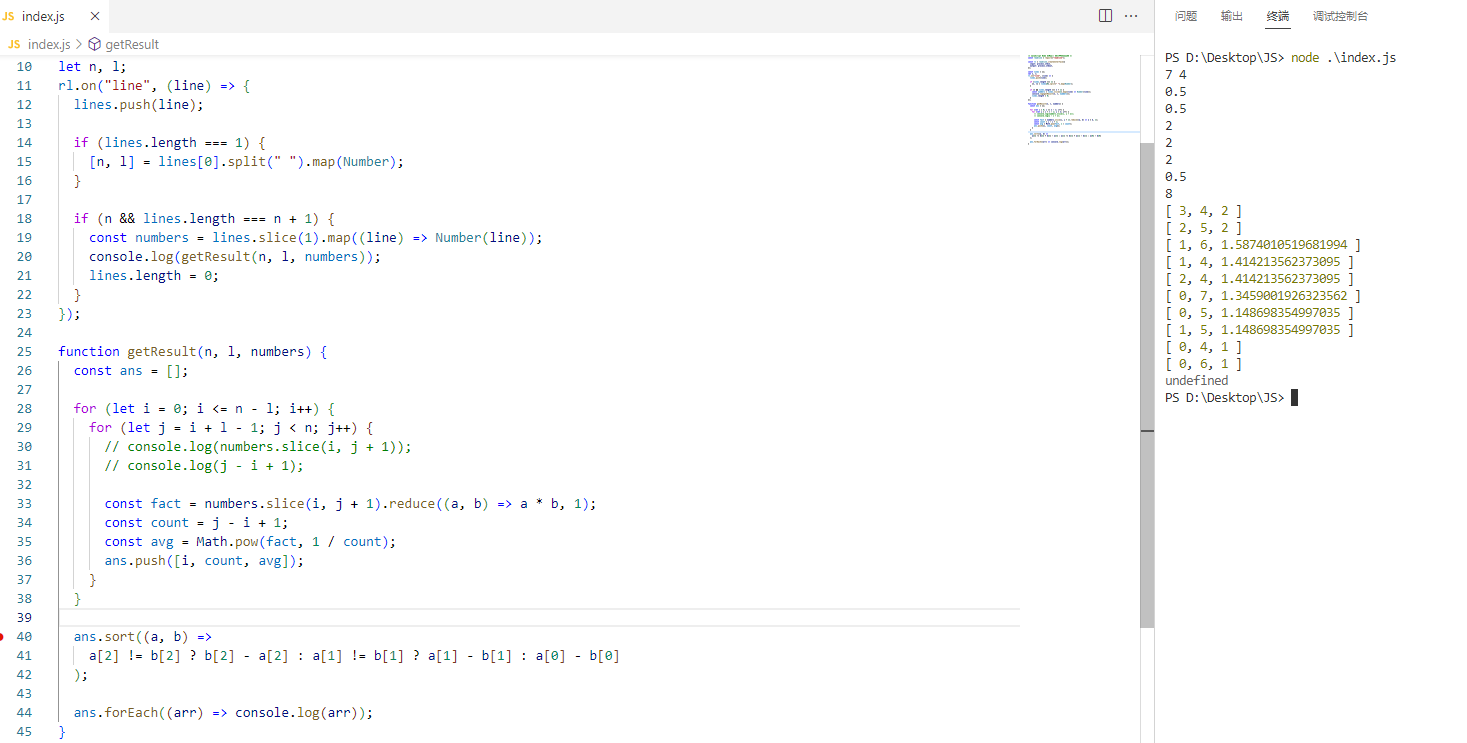
可以发现:
- 起始索引3,长度4的子数组的几何平均值是2
- 起始索引2,长度5的子数组的几何平均值也是2
但是对于本题而言:
若有多个子数组的几何平均值均为最大值,则输出长度最小的子数组。
若有多个长度相同的子数组的几何平均值均为最大值,则输出最前面的子数组。
因此,起始索引3,长度4的子数组是最优解,因为该子数组的长度更短。因此上面用例应该输出3 4。
但是前面的 “二分+前缀积” 解法输出的是2 5
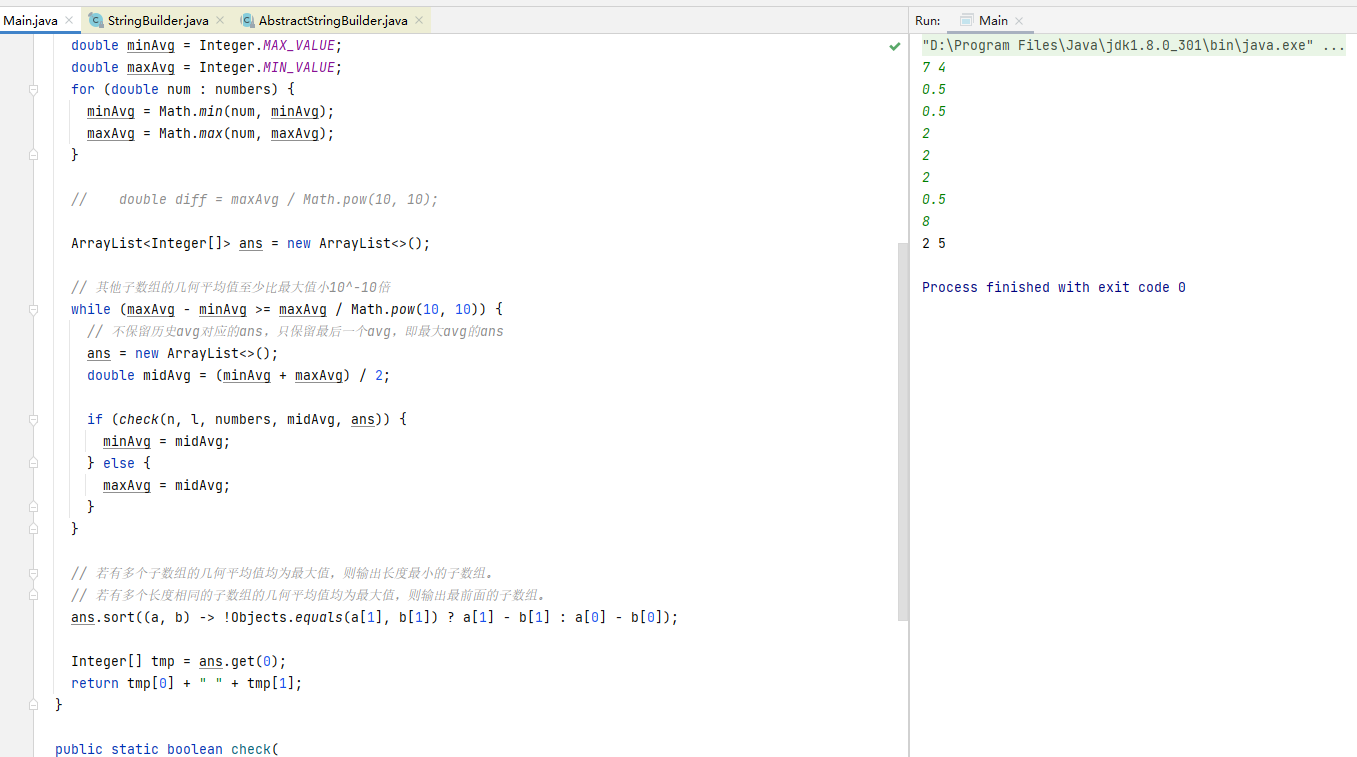
明明已经考虑了会存在 “多个子数组的几何平均值均为最大值” 的情况,为啥会得出错误答案呢?
比如下面min_pre_fact代表的时0~i-L范围内最小的子数组(注意,是范围内,不一定就是0~i-L),而fact代表的是0~i子数组,然后用fact / min_pre_fact 其实就能得出一个长度大于L的子数组的几何平均值/avg的情况
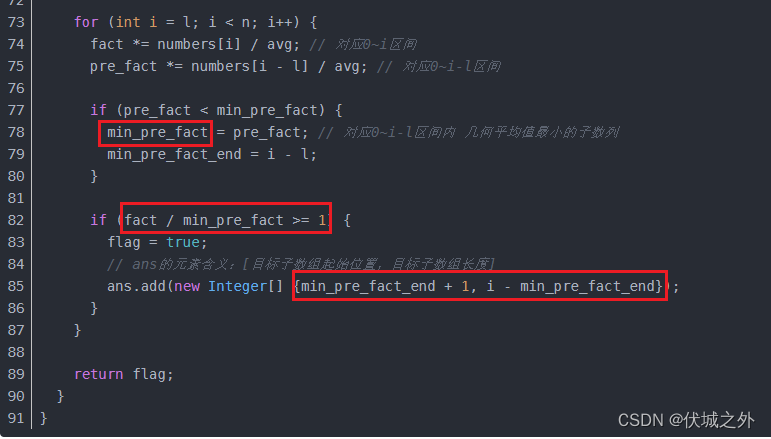
因此,check函数在验证几何平均值时,并非验证了所有子数组,而这是验证了一些特定,最优情况的子数组,因此上面代码中ans统计到的子数组是不全面的。
我想了一下,本题没有什么好的解法,我们只能暴力枚举所有子数组情况,并求出每个子数组的几何平均值,保留最大的,如果存在多个最大几何平均值子数组,那么就保留长度最短的,如果有多个长度相同的,则保留起始索引最靠前的。
当然,在暴力枚举所有子数组情况前,可以先求解出输入数组的前缀积数组,然后基于前缀积数组,就可以求解出任意范围子数组的积了。
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int l = sc.nextInt();
double[] numbers = new double[n];
for (int i = 0; i < n; i++) {
numbers[i] = sc.nextDouble();
}
System.out.println(getResult(n, l, numbers));
}
public static String getResult(int n, int l, double[] numbers) {
// dp是“前缀积”数组
double[] dp = new double[n];
dp[0] = numbers[0];
for (int i = 1; i < n; i++) {
dp[i] = numbers[i] * dp[i - 1];
}
// 记录题解
Avg ans = null;
// 长度大于L的子数组的起始位置start,和结束位置end,注意这里end是包含的,即左闭右闭
for (int start = 0; start <= n - l; start++) {
for (int end = start + l - 1; end < n; end++) {
// 通过前缀积数组,快速计算出start~end范围对应子数组的元素之积
double fact = start == 0 ? dp[end] : dp[end] / dp[start - 1];
// k是当前start~end子数组的长度
int k = end - start + 1;
Avg cur = new Avg(start, k, fact);
// 保留几何平均值最大的,如果几何平均值相同,则保留长度较小的,如果长度相同则保留起始位置最靠前的
if (ans == null || Avg.cmp(ans, cur) > 0) ans = cur;
}
}
return ans.start + " " + ans.root;
}
}
class Avg {
int start;
int root;
double fact;
double avg;
public Avg(int start, int root, double fact) {
this.start = start;
this.root = root;
this.fact = fact;
// 几何平均值
this.avg = Math.pow(fact, 1.0 / root);
}
public static int cmp(Avg a, Avg b) {
// 由于题目说几何平均值间最小差距为
if (Math.abs(a.avg - b.avg) > Math.max(a.avg, b.avg) / Math.pow(10, 10)) {
// 保留几何平均值最大的
return b.avg - a.avg > 0 ? 1 : -1;
}
// 如果几何平均值相同,则保留长度较小的
if (a.root != b.root) return a.root - b.root;
// 如果长度相同则保留起始位置最靠前的
return a.start - b.start;
}
}
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, l;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
[n, l] = lines[0].split(" ").map(Number);
}
if (n && lines.length === n + 1) {
const numbers = lines.slice(1).map((line) => Number(line));
console.log(getResult(n, l, numbers));
lines.length = 0;
}
});
function getResult(n, l, numbers) {
// dp是“前缀积”数组
const dp = new Array(n).fill(0);
dp[0] = numbers[0];
for (let i = 1; i < n; i++) {
dp[i] = numbers[i] * dp[i - 1];
}
// 记录题解
let ans = null;
// 长度大于L的子数组的起始位置start,和结束位置end,注意这里end是包含的,即左闭右闭
for (let start = 0; start <= n - l; start++) {
for (let end = start + l - 1; end < n; end++) {
// 通过前缀积数组,快速计算出start~end范围对应子数组的元素之积
const fact = start == 0 ? dp[end] : dp[end] / dp[start - 1];
// k是当前start~end子数组的长度
const k = end - start + 1;
const cur = new Avg(start, k, fact);
// 保留几何平均值最大的,如果几何平均值相同,则保留长度较小的,如果长度相同则保留起始位置最靠前的
if (ans == null || cmp(ans, cur) > 0) ans = cur;
}
}
return ans.start + " " + ans.root;
}
function cmp(a, b) {
// 由于题目说几何平均值间最小差距为
if (Math.abs(a.avg - b.avg) > Math.max(a.avg, b.avg) / Math.pow(10, 10)) {
// 保留几何平均值最大的
return b.avg - a.avg > 0 ? 1 : -1;
}
// 如果几何平均值相同,则保留长度较小的
if (a.root != b.root) return a.root - b.root;
// 如果长度相同则保留起始位置最靠前的
return a.start - b.start;
}
class Avg {
constructor(start, root, fact) {
this.start = start;
this.root = root;
this.fact = fact;
// 几何平均值
this.avg = Math.pow(fact, 1 / root);
}
}
Python算法源码
# 输入获取
n, l = map(int, input().split())
numbers = [float(input()) for i in range(n)]
class Avg:
def __init__(self, start, root, fact):
self.start = start
self.root = root
self.fact = fact
# 几何平均值
self.avg = pow(fact, 1.0 / root)
def cmp(a, b):
# 由于题目说几何平均值间最小差距为
if abs(a.avg - b.avg) > max(a.avg, b.avg) / pow(10, 10):
# 保留几何平均值最大的
return 1 if b.avg - a.avg > 0 else -1
# 如果几何平均值相同,则保留长度较小的
if a.root != b.root:
return a.root - b.root
# 如果长度相同则保留起始位置最靠前的
return a.start - b.start
# 算法入口
def getResult(n, l, numbers):
# dp是“前缀积”数组
dp = [0] * n
dp[0] = numbers[0]
for i in range(1, n):
dp[i] = numbers[i] * dp[i - 1]
# 记录题解
ans = None
# 长度大于L的子数组的起始位置start,和结束位置end,注意这里end是包含的,即左闭右闭
for start in range(n - l + 1):
for end in range(start + l - 1, n):
# 通过前缀积数组,快速计算出start~end范围对应子数组的元素之积
fact = dp[end] if start == 0 else dp[end] / dp[start - 1]
# k是当前start~end子数组的长度
k = end - start + 1
cur = Avg(start, k, fact)
# 保留几何平均值最大的,如果几何平均值相同,则保留长度较小的,如果长度相同则保留起始位置最靠前的
if ans is None or cmp(ans, cur) > 0:
ans = cur
return str(ans.start) + " " + str(ans.root)
# 算法调用
print(getResult(n, l, numbers))
免责声明:
评论0