当前位置： 2024华为OD机试题库 (A卷,200分)- 基站维护工程师（Java & JS & Python）

(A卷,200分)- 基站维护工程师（Java & JS & Python）

2024-05-07 14

题目描述

小王是一名基站维护工程师，负责某区域的基站维护。
某地方有  n  个基站(1 < n < 10)，已知各基站之间的距离 s(0 < s < 500)，并且基站 x 到基站 y 的距离，与基站 y 到基站 x 的距离并不一定会相同。
小王从基站 1 出发，途经每个基站 1 次，然后返回基站 1 ，需要请你为他选择一条距离最短的路。

输入描述

站点数n和各站点之间的距离(均为整数)

输出描述

最短路程的数值

用例

输入 3
0 2 1
1 0 2
2 1 0
输出 3
说明 无

题目解析

用例输入含义是，

3            //有3个基站，
0 2 1      // 站点1到站点1的距离0，到站点2的距离2，到站点3的距离1
1 0 2      // 站点2到站点1的距离1，到站点2的距离0，到站点3的距离2
2 1 0      // 站点3到站点1的距离2，到站点2的距离1，到站点3的距离0

图示如下

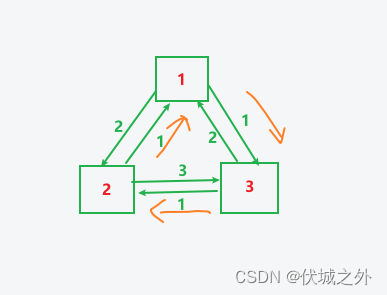
可以发现，1 → 3  → 2  → 1 的路线距离是最短的，只有3距离。

题目中说：

小王从基站 1 出发，途经每个基站 1 次，然后返回基站 1

并且按照题目输入来看，每个站点都与剩下的其他站点相连，因此本题其实就是求解n-1个站点（即2~n站点，起始站点1）的全排列。

比如用例一共三个站点，从1站点出发，即求2，3站点的全排列：23，32

因此一共有两种途径选择：1 → 2 → 3 → 1 和  1 → 3 → 2 → 1

我们只要比较各排列路径中距离最小的即为题解。

两个站点i，j之间距离，即为matrix[i-1][j-1]，比如求解1 → 2距离，起始就是matrix[0][1]。

题目中说 1 < n < 10 ，也就是说最多有9个站点，而我们求解n-1个站点的全排列，即8个站点的全排列，一共有8！= 40320 个，每个排列求解距离要进行一个O(n)的遍历，即9次遍历。因此一共是差不多40w次循环，好在没什么计算量。

我测试了一下10*10矩阵的用时为200ms左右，应该符合要求。

JavaScript算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let n;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    n = lines[0] - 0;
  }

  if (n && lines.length === n + 1) {
    lines.shift();
    const matrix = lines.map((line) => line.split(" ").map(Number));
    console.log(getResult(matrix, n));
    lines.length = 0;
  }
});

function getResult(matrix, n) {
  const res = [];
  dfs(n, [], [], res);

  let ans = Infinity;

  for (let path of res) {
    let dis = matrix[0][path[0]];
    path.reduce((p, c) => {
      dis += matrix[p][c];
      return c;
    });
    dis += matrix[path.at(-1)][0];
    ans = Math.min(ans, dis);
  }

  return ans;
}

function dfs(n, used, path, res) {
  if (path.length === n - 1) return res.push([...path]);

  for (let i = 1; i < n; i++) {
    if (!used[i]) {
      path.push(i);
      used[i] = true;
      dfs(n, used, path, res);
      used[i] = false;
      path.pop();
    }
  }
}

上面代码可能会爆内存，改进代码如下

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let n;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    n = lines[0] - 0;
  }

  if (n && lines.length === n + 1) {
    lines.shift();
    const matrix = lines.map((line) => line.split(" ").map(Number));
    console.log(getResult(matrix, n));
    lines.length = 0;
  }
});

function getResult(matrix, n) {
  const ans = { val: Infinity };
  dfs(n, [], [], ans, matrix);

  return ans.val;
}

function dfs(n, used, path, ans, matrix) {
  if (path.length === n - 1) {
    let dis = matrix[0][path[0]];
    path.reduce((p, c) => {
      dis += matrix[p][c];
      return c;
    });
    dis += matrix[path.at(-1)][0];
    ans.val = Math.min(ans.val, dis);
    return;
  }

  for (let i = 1; i < n; i++) {
    if (!used[i]) {
      path.push(i);
      used[i] = true;
      dfs(n, used, path, ans, matrix);
      used[i] = false;
      path.pop();
    }
  }
}

 

Java算法源码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();

        int[][] matrix = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                matrix[i][j] = sc.nextInt();
            }
        }

        System.out.println(getResult(matrix, n));
    }

    public static int getResult(int[][] matrix, int n) {
        boolean[] used = new boolean[n];
        LinkedList<Integer> path = new LinkedList<>();
        ArrayList<LinkedList<Integer>> res = new ArrayList<>();

        dfs(n, used, path, res);

        int ans = Integer.MAX_VALUE;

        for (LinkedList<Integer> pa : res) {
            int dis = matrix[0][pa.get(0)];
            for (int i = 0; i < pa.size() - 1; i++) {
                int p = pa.get(i);
                int c = pa.get(i + 1);
                dis += matrix[p][c];
            }
            dis += matrix[pa.getLast()][0];
            ans = Math.min(ans, dis);
        }

        return ans;
    }

    public static void dfs(int n, boolean[] used, LinkedList<Integer> path, ArrayList<LinkedList<Integer>> res) {
        if (path.size() == n - 1) {
            res.add((LinkedList<Integer>)path.clone());
            return;
        }

        for (int i = 1; i < n; i++) {
            if (!used[i]) {
                path.push(i);
                used[i] = true;
                dfs(n, used, path, res);
                used[i] = false;
                path.pop();
            }
        }
    }

}

上面代码有爆内存的风险，改进代码如下

import java.util.LinkedList;
import java.util.Scanner;

public class Main {
  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);

    int n = sc.nextInt();

    int[][] matrix = new int[n][n];
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < n; j++) {
        matrix[i][j] = sc.nextInt();
      }
    }

    System.out.println(getResult(matrix, n));
  }

  public static int getResult(int[][] matrix, int n) {
    boolean[] used = new boolean[n];
    LinkedList<Integer> path = new LinkedList<>();
    int[] ans = {Integer.MAX_VALUE};

    dfs(n, used, path, ans, matrix);

    return ans[0];
  }

  public static void dfs(
      int n, boolean[] used, LinkedList<Integer> path, int[] ans, int[][] matrix) {
    if (path.size() == n - 1) {
      int dis = matrix[0][path.get(0)];
      for (int i = 0; i < path.size() - 1; i++) {
        int p = path.get(i);
        int c = path.get(i + 1);
        dis += matrix[p][c];
      }
      dis += matrix[path.getLast()][0];
      ans[0] = Math.min(ans[0], dis);
      return;
    }

    for (int i = 1; i < n; i++) {
      if (!used[i]) {
        path.push(i);
        used[i] = true;
        dfs(n, used, path, ans, matrix);
        used[i] = false;
        path.pop();
      }
    }
  }
}

Python算法源码

import sys

# 输入获取
n = int(input())
matrix = [list(map(int, input().split())) for i in range(n)]


# 算法入口
def getResult(matrix, n):
    res = []
    dfs(n, [False] * n, [], res)

    ans = sys.maxsize

    for path in res:
        dis = matrix[0][path[0]]
        for i in range(len(path) - 1):
            dis += matrix[path[i]][path[i + 1]]
        dis += matrix[path[-1]][0]
        ans = min(ans, dis)

    return ans


def dfs(n, used, path, res):
    if len(path) == n - 1:
        return res.append(path[:])

    for i in range(1, n):
        if not used[i]:
            path.append(i)
            used[i] = True
            dfs(n, used, path, res)
            used[i] = False
            path.pop()


# 算法调用
print(getResult(matrix, n))

上面代码有爆内存的风险，改进代码如下：

import sys

# 输入获取
n = int(input())
matrix = [list(map(int, input().split())) for i in range(n)]


# 算法入口
def getResult():
    ans = [sys.maxsize]
    dfs(n, [False] * n, [], ans)

    return ans[0]


def dfs(n, used, path, ans):
    if len(path) == n - 1:
        dis = matrix[0][path[0]]
        for i in range(len(path) - 1):
            dis += matrix[path[i]][path[i + 1]]
        dis += matrix[path[-1]][0]
        ans[0] = min(ans[0], dis)
        return

    for i in range(1, n):
        if not used[i]:
            path.append(i)
            used[i] = True
            dfs(n, used, path, ans)
            used[i] = False
            path.pop()


# 算法调用
print(getResult())

免责声明：

1、IT资源小站为非营利性网站，全站所有资料仅供网友个人学习使用，禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享，本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题，请立即告知本站，本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体，但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员，一律视为同意网站规定，本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文

0

评论0

取消

首页 发现 VIP 我的

站点公告

没有账号？注册  忘记密码？