题目描述
公元2919年，人类终于发现了一颗宜居星球——X星。
现想在X星一片连绵起伏的山脉间建一个天热蓄水库，如何选取水库边界，使蓄水量最大？
要求：
- 山脉用正整数数组s表示，每个元素代表山脉的高度。
- 选取山脉上两个点作为蓄水库的边界，则边界内的区域可以蓄水，蓄水量需排除山脉占用的空间
- 蓄水量的高度为两边界的最小值。
- 如果出现多个满足条件的边界，应选取距离最近的一组边界。
输出边界下标（从0开始）和最大蓄水量；如果无法蓄水，则返回0，此时不返回边界。
例如，当山脉为s=[3,1,2]时，则选取s[0]和s[2]作为水库边界，则蓄水量为1，此时输出：0 2:1
当山脉s=[3,2,1]时，不存在合理的边界，此时输出：0。
输入描述
一行正整数，用空格隔开，例如输入
1 2 3
表示s=[1,2,3]
输出描述
当存在合理的水库边界时，输出左边界、空格、右边界、英文冒号、蓄水量；例如
0 2:1
当不存在合理的书库边界时，输出0；例如
0
备注
- 1 ≤ length(s) ≤ 10000
- 0 ≤ s[i] ≤ 10000
用例
| 输入 | 1 9 6 2 5 4 9 3 7 |
| 输出 | 1 6:19 |
| 说明 | 经过分析，选取s[1]和s[6]，水库蓄水量为19（3+7+4+5） |
| 输入 | 1 8 6 2 5 4 8 3 7 |
| 输出 | 1 6:15 |
| 说明 | 经过分析，选取s[1]和s[8]时，水库蓄水量为15；同样选取s[1]和s[6]时，水库蓄水量也为15。由于后者下标距离小（为5），故应选取后者。 |
| 输入 | 1 2 3 |
| 输出 | 0 |
| 说明 | 不存在合理的水库边界 |
题目解析
用例1图示如下：
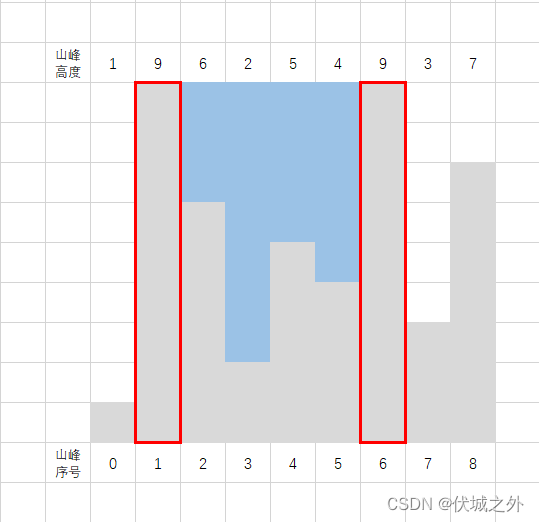
选择山峰1和山峰6作为边界，则可获得最大蓄水量19
用例2图示如下
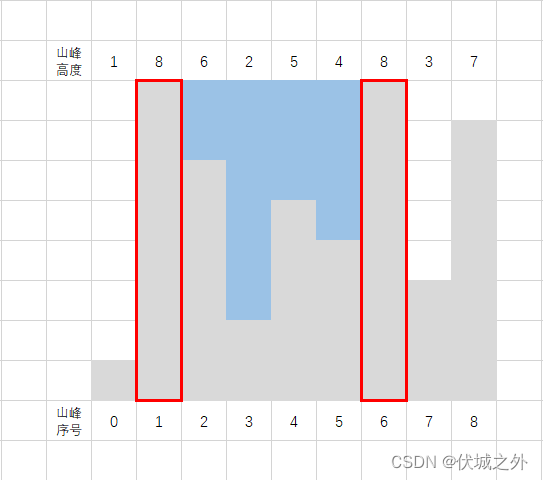
选择山峰1和山峰6作为边界，则可获得最大蓄水量15
其实用例2还可以选择山峰1和山峰8作为边界，也可以获得最大蓄水量15，如下图所示
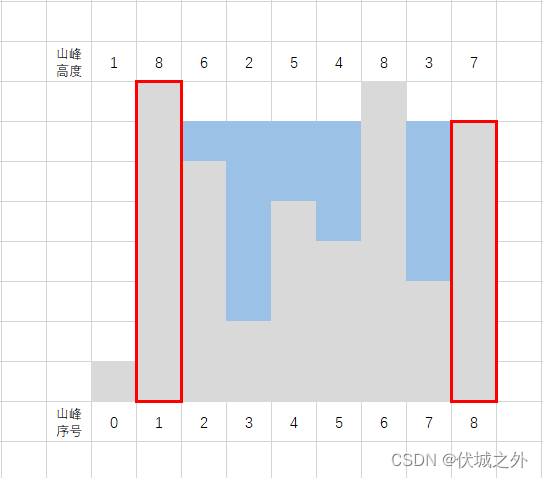
但是此时两边界山峰的距离是6，相较于选择山峰1，6作为边界时距离4而言，更远。
按照题目要求，我们需要找到：蓄水量最大的，且距离最近的两个边界山峰。
我一开始的解题思路是双指针，类似于下面这题
但是经过如下几个用例测试，发现本题无法像上面链接题目一样找到一个O(n)的解法，双边指针无法找到一个固定的策略进行运动。
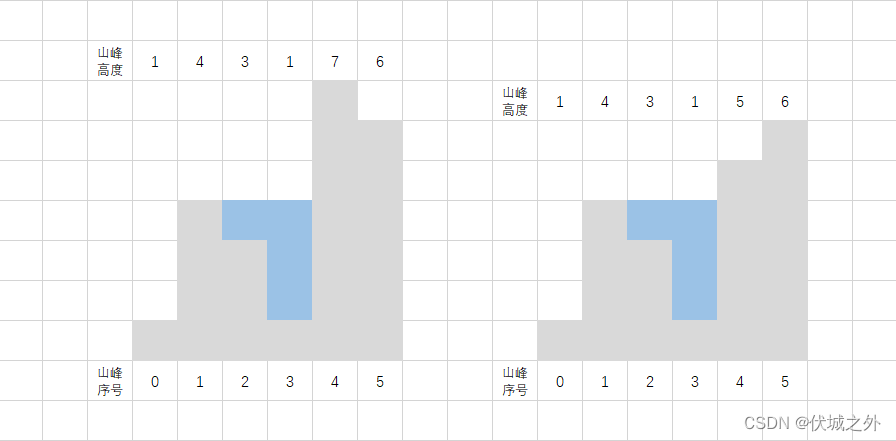
因此，我开始寻找其他的思路，直到发现了LeetCode – 42 接雨水_伏城之外的博客-CSDN博客
其实，我们不应该从横向来思考本题，可以从纵向来思考本题。什么意思呢？
我们按照接雨水那个思路，把用例1中所有能接水的山峰全部接满，即如下图所示
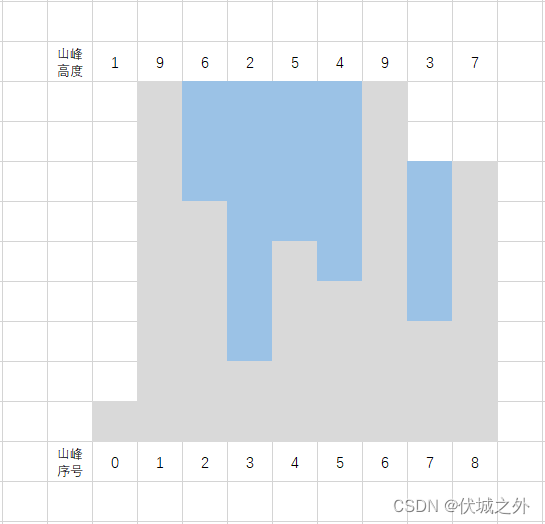
此时从纵向来看只有有两条水位线，如下图所示
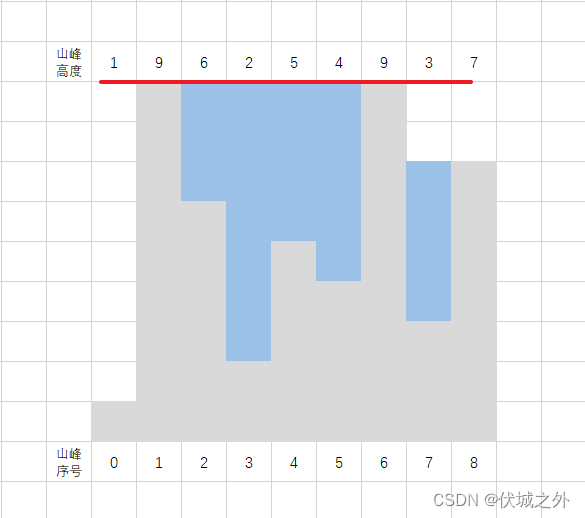
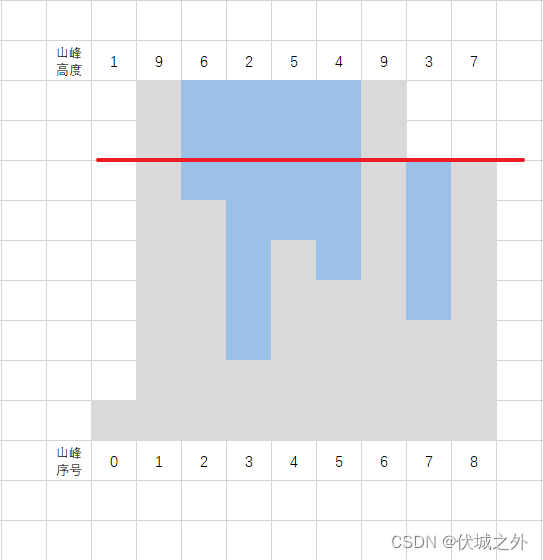
从上图可以看出，每条水位线都有都可能与多个山峰相交，但是我们只需要关注：
- 两端的
- 能够达到该水位线要求得山峰
如下图所示：
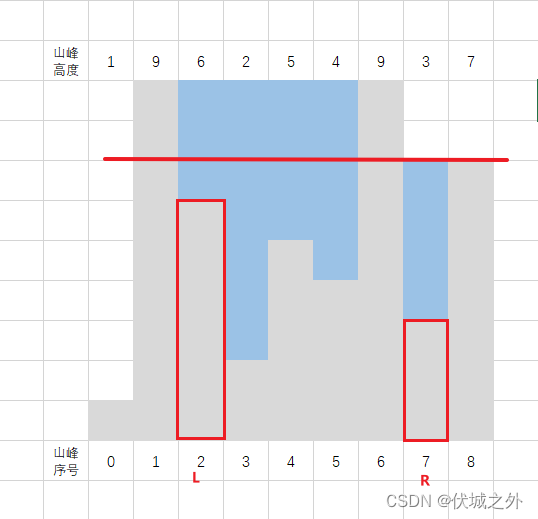
上图中，L山峰和R山峰是可以达到该水位线要求的最外层的两端山峰，此时这两座山峰之间的每个山峰的储水量就是该水位线最大的储水量。
而此时边界山峰为L-1，和R+1。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const h = line.split(" ").map(Number);
console.log(getResult(h));
});
function getResult(h) {
const n = h.length;
// left[i] 记录 第 i 个山峰左边的最高山峰
const left = new Array(n).fill(0);
for (let i = 1; i < n; i++) {
left[i] = Math.max(left[i - 1], h[i - 1]);
}
// right[i] 记录 第 i 个山峰右边的最高山峰
const right = new Array(n).fill(0);
for (let i = n - 2; i >= 0; i--) {
right[i] = Math.max(right[i + 1], h[i + 1]);
}
// lines[i] 记录 第 i 个山峰的水位线高度
const lines = new Array(n).fill(0);
// lineSet记录有哪些水位线
const lineSet = new Set();
for (let i = 1; i < n - 1; i++) {
const water = Math.max(0, Math.min(left[i], right[i]) - h[i]); // water 记录 第 i 个山峰可以储存多少水
if (water != 0) {
// 第 i 个山峰的水位线高度
lines[i] = water + h[i];
lineSet.add(lines[i]);
}
}
// ans数组含义：[左边界， 右边界， 储水量]
let ans = [0, 0, 0];
// 遍历每一个水位线
for (let line of lineSet) {
// 满足该水位线的最左侧山峰位置l
let l = 0;
while (lines[l] < line || h[l] >= line) {
l++;
}
// 满足该水位线的最右侧山峰位置r
let r = n - 1;
while (lines[r] < line || h[r] >= line) {
r--;
}
// 该水位线的总储水量
let sum = 0;
for (let i = l; i <= r; i++) {
sum += Math.max(0, line - h[i]);
}
// 记录最大的储水量
if (sum > ans[2]) {
ans[0] = l - 1;
ans[1] = r + 1;
ans[2] = sum;
}
// 如果有多个最多储水量选择，则选择边界山峰距离最短的
else if (sum == ans[2]) {
const curDis = r - l + 1;
const minDis = ans[1] - ans[0] - 1;
if (curDis < minDis) {
ans[0] = l - 1;
ans[1] = r + 1;
}
}
}
if (ans[2] == 0) return "0";
return ans[0] + " " + ans[1] + ":" + ans[2];
}
Java算法源码
import java.util.Arrays;
import java.util.HashSet;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Integer[] h =
Arrays.stream(sc.nextLine().split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
System.out.println(getResult(h));
}
public static String getResult(Integer[] h) {
int n = h.length;
// left[i] 记录 第 i 个山峰左边的最高山峰
int[] left = new int[n];
for (int i = 1; i < n; i++) left[i] = Math.max(left[i - 1], h[i - 1]);
// right[i] 记录 第 i 个山峰右边的最高山峰
int[] right = new int[n];
for (int i = n - 2; i >= 0; i--) right[i] = Math.max(right[i + 1], h[i + 1]);
// lines[i] 记录 第 i 个山峰的水位线高度
int[] lines = new int[n];
// lineSet记录有哪些水位线
HashSet<Integer> lineSet = new HashSet<>();
for (int i = 1; i < n - 1; i++) {
int water = Math.max(0, Math.min(left[i], right[i]) - h[i]); // water 记录 第 i 个山峰可以储存多少水
if (water != 0) {
// 第 i 个山峰的水位线高度
lines[i] = water + h[i];
lineSet.add(lines[i]);
}
}
// ans数组含义：[左边界， 右边界， 储水量]
int[] ans = {0, 0, 0};
// 遍历每一个水位线
for (int line : lineSet) {
// 满足该水位线的最左侧山峰位置l
int l = 0;
while (lines[l] < line || h[l] >= line) {
l++;
}
// 满足该水位线的最右侧山峰位置r
int r = n - 1;
while (lines[r] < line || h[r] >= line) {
r--;
}
// 该水位线的总储水量
int sum = 0;
for (int i = l; i <= r; i++) {
sum += Math.max(0, line - h[i]);
}
// 记录最大的储水量
if (sum > ans[2]) {
ans[0] = l - 1;
ans[1] = r + 1;
ans[2] = sum;
}
// 如果有多个最多储水量选择，则选择边界山峰距离最短的
else if (sum == ans[2]) {
int curDis = r - l + 1;
int minDis = ans[1] - ans[0] - 1;
if (curDis < minDis) {
ans[0] = l - 1;
ans[1] = r + 1;
}
}
}
if (ans[2] == 0) return "0";
return ans[0] + " " + ans[1] + ":" + ans[2];
}
}
Python算法源码
# 输入获取
h = list(map(int, input().split()))
# 算法入口
def getResult(h):
n = len(h)
# left[i] 记录 第 i 个山峰左边的最高山峰
left = [0] * n
for i in range(1, n):
left[i] = max(left[i - 1], h[i - 1])
# right[i] 记录 第 i 个山峰右边的最高山峰
right = [0] * n
for i in range(n - 2, -1, -1):
right[i] = max(right[i + 1], h[i + 1])
# lines[i] 记录 第 i 个山峰的水位线高度
lines = [0] * n
# lineSet记录有哪些水位线
lineSet = set()
for i in range(1, n - 1):
# water 记录 第 i 个山峰可以储存多少水
water = max(0, min(left[i], right[i]) - h[i])
# 如果第 i 个山峰可以储存水，则必然有一个水位线，记录到lines中
if water != 0:
# 第 i 个山峰的水位线高度
lines[i] = water + h[i]
lineSet.add(lines[i])
# ans数组含义：[左边界， 右边界， 储水量]
ans = [0, 0, 0]
# 遍历每一个水位线
for line in lineSet:
# 满足该水位线的最左侧山峰位置l
l = 0
while lines[l] < line or h[l] >= line:
l += 1
# 满足该水位线的最右侧山峰位置r
r = n - 1
while lines[r] < line or h[r] >= line:
r -= 1
# 该水位线的总储水量
total = 0
for i in range(l, r + 1):
total += max(0, line - h[i])
# 记录最大的储水量
if total > ans[2]:
ans[0] = l - 1
ans[1] = r + 1
ans[2] = total
# 如果有多个最多储水量选择，则选择边界山峰距离最短的
elif total == ans[2]:
curDis = r - l + 1
minDis = ans[1] - ans[0] - 1
if curDis < minDis:
ans[0] = l - 1
ans[1] = r + 1
if ans[2] == 0:
return "0"
return str(ans[0]) + " " + str(ans[1]) + ":" + str(ans[2])
# 算法调用
print(getResult(h))
免责声明：
1、IT资源小站为非营利性网站，全站所有资料仅供网友个人学习使用，禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享，本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题，请立即告知本站，本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体，但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员，一律视为同意网站规定，本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0