题目描述
当小区通信设备上报警时，系统会自动生成待处理的工单，华为工单调度系统需要根据不同的策略，调度外线工程师（FME）上站修复工单对应的问题。
根据与运营商签订的合同，不同严重程度的工单被处理并修复的时长要求不同，这个要求被修复的时长我们称之为SLA时间。
假设华为和运营商A签订了运维合同，部署了一套调度系统，只有1个外线工程师（FME），每个工单根据问题严重程度会给一个评分，在SLA时间内完成修复的工单，华为获得工单评分对应的积分，超过SLA完成的工单不获得积分，但必须完成该工单。运营商最终会根据积分进行付款。
请设计一种调度策略，根据现状得到调度结果完成所有工单，让这个外线工程师处理的工单获得的总积分最多。
假设从某个调度时刻开始，当前工单数量为N，不会产生新的工单，每个工单处理修复耗时为1小时，请设计你的调度策略，完成业务目标。
不考虑外线工程师在小区之间行驶的耗时。
输入描述
第一行为一个整数N，表示工单的数量。
接下来N行，每行包括两个整数。第一个整数表示工单的SLA时间（小时），第二个数表示该工单的积分。
输出描述
输出一个整数表示可以获得的最大积分。
备注
- 工单数量N ≤ 10^6
- SLA时间 ≤ 7 * 10^5
- 答案的最大积分不会超过2147483647
用例
假设有7个工单的SLA时间（小时）和积分如下：
| 工单编号 | SLA | 积分 |
| 1 | 1 | 6 |
| 2 | 1 | 7 |
| 3 | 3 | 2 |
| 4 | 3 | 1 |
| 5 | 2 | 4 |
| 6 | 2 | 5 |
| 7 | 6 | 1 |
| 输入 | 7 1 6 1 7 3 2 3 1 2 4 2 5 6 1 |
| 输出 | 15 |
| 说明 | 最多可获得15积分，其中一个调度结果完成工单顺序为2，6，3，1，7，5，4（可能还有其他顺序） |
题目解析
用例的含义如下
从现在开始：
- 编号1和2的工单，需要在1小时内完成
- 编号5和6的工单，需要在2小时内完成
- 编号3和4的工单，需要在3小时内完成
- 编号7的工单，需要在6小时内完成
如果现在是0点，那么有时间线如下：
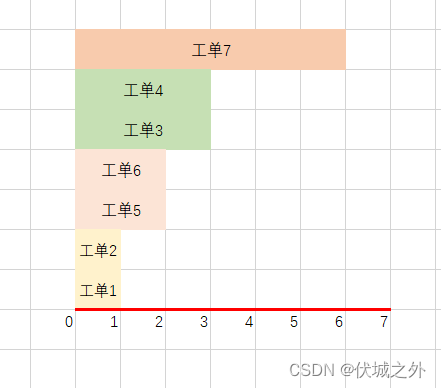
但是每个工单都需要花费1小时来修复，因此：
- 0~1点之间，工单1和工单2是最优先的，因为超过这个时间，他们即使修复了也没有积分了，但是由于每个工单都需要1小时，因此这个时间段内，只有一个工单可以被修复，另一个工单需要被放弃，此时我们应该选择积分最多的工单2（7个积分）来优先修复。
因此这个时间段可以获得7个积分。
- 1~2点之间，工单5和工单6是最优先的，但是由于只有1小时，因此只能修复一个工单，优先选择积分高的工单6（5个积分）来修复。而工单5因为超时所以放弃。
因此这个时间段可以获得5个积分。
- 2~3点之间，工单3和工单4是最优先的，但是由于只有1小时，因此只能修复一个工单，优先选择积分高的工单3（2个积分）来修复。而工单4因为超时所以放弃。
因此这个时间段可以获得2个积分。
- 3~5点之间，没有紧急工单，这个时间可以处理2个工单，而之前放弃的工单数量有3个，因此我们可以在这段时间内选择处理任意两个放弃掉的工单，但是没有积分拿。
- 5~6点之间，有一个紧急工单7，因此我们修复工单7，拿1个积分。
因此这个时间段可以获得1个积分。
- 6~7之间，没有紧急工单，这个时间可以处理1个工单，而之前放弃的工单数量还剩一个，因此我们可以在这段时间选择处理剩下一个被放弃工单，但是没有积分拿。
最终可以拿到 7 + 5 + 2 + 1 = 15个积分。
另外，还有一些其他网友提供的用例如：
3
1 1
2 10
2 20
当0~1点时，虽然工单1是最紧急的，但是放弃工单1，而是在0~2点执行工单2和3可以获得最大积分30。
那么上面逻辑该如何实现呢？
本题的解题思路可以参照
我的解题思路如下：
首先将所有工单wos按照截止时间升序，即最紧急的排在最前面。
然后创建一个优先队列pq（按照积分升序，即积分少的工单在堆顶），定义一个当前时间curTime = 0，定义一个ans记录拿到的积分，然后遍历升序后的wos的每一个wo并尝试加入pq中，此时会出现两种情况：
- 要加入pq的工单wo的截止时间endTime >= curTime + 1，表示当前花一小时修复该工单后，依旧在工单的有效期内，此时我们可以之间将wo加入pq，并且获得该工单的积分 ans += score，然后curTime++
- 要加入pq的工单wo的截止时间endTime < curTime + 1，表示当前花一个小时修复该工单后，超出了该工单的有效期，此时我们需要比较 优先队列堆顶的工单A的积分（优先队列中最小积分）和 要加入的B工单的积分：
- 如果B > A，则说明当前B工单更具有修复价值，因此我们应该把修复工单A的一小时用来修复B工单，因此优先队列弹出顶部工单A，并加入工单B。此时 ans += B.score – A.score，而curTime不变，因为只是将原本用于修复A的一小时，换到修复B上。
- 如果B <= A，则说明当前B工单不比A更具有修复价值。
对于JS而言没有原生的优先队列实现类，基于堆结构实现的优先队列请看：LeetCode – 1705 吃苹果的最大数目_伏城之外的博客-CSDN博客
如果觉得实现过于麻烦，也可以使用有序数组实现优先队列，但是维持优先级的时间复杂度将从O(lgN)升到O(N)
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
n = lines[0] - 0;
}
if (n && lines.length === n + 1) {
const wos = lines.slice(1).map((line) => line.split(" ").map(Number));
console.log(getResult(n, wos));
lines.length = 0;
}
});
/**
* @param {*} n 工单数量
* @param {*} wos 工单的 [SLA, 积分]
* @returns 可以获得的最大积分
*/
function getResult(n, wos) {
// 按照SLA截止时间升序
wos.sort((a, b) => a[0] - b[0]);
const pq = new PriorityQueue((a, b) => a - b);
let curTime = 0;
let ans = 0;
for (let wo of wos) {
const [endTime, score] = wo;
if (endTime >= curTime + 1) {
pq.offer(score);
ans += score;
curTime++;
} else {
if (pq.size() == 0) {
continue;
}
const min_score = pq.peek();
if (score > min_score) {
pq.poll();
pq.offer(score);
ans += score - min_score;
}
}
}
return ans;
}
// 基于堆实现优先队列
class PriorityQueue {
constructor(cpr) {
this.queue = [];
this.cpr = cpr;
}
swap(a, b) {
const tmp = this.queue[a];
this.queue[a] = this.queue[b];
this.queue[b] = tmp;
}
// 上浮
swim() {
let c = this.queue.length - 1;
while (c >= 1) {
const f = Math.floor((c - 1) / 2);
if (this.cpr(this.queue[c], this.queue[f]) < 0) {
this.swap(c, f);
c = f;
} else {
break;
}
}
}
// 入队
offer(val) {
this.queue.push(val);
this.swim();
}
// 下沉
sink() {
let f = 0;
while (true) {
let c1 = 2 * f + 1;
let c2 = c1 + 1;
let c;
let val1 = this.queue[c1];
let val2 = this.queue[c2];
if (val1 && val2) {
c = this.cpr(val1, val2) < 0 ? c1 : c2;
} else if (val1 && !val2) {
c = c1;
} else if (!val1 && val2) {
c = c2;
} else {
break;
}
if (this.cpr(this.queue[c], this.queue[f]) < 0) {
this.swap(c, f);
f = c;
} else {
break;
}
}
}
// 出队
poll() {
this.swap(0, this.queue.length - 1);
const res = this.queue.pop();
this.sink();
return res;
}
peek() {
return this.queue[0];
}
size() {
return this.queue.length;
}
}
Java算法源码
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] wos = new int[n][2];
for (int i = 0; i < n; i++) {
wos[i][0] = sc.nextInt();
wos[i][1] = sc.nextInt();
}
System.out.println(getResult(n, wos));
}
/**
* @param n 工单数量
* @param wos 工单的 [SLA, 积分]
* @return 可以获得的最大积分
*/
public static int getResult(int n, int[][] wos) {
Arrays.sort(wos, (a, b) -> a[0] - b[0]);
PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> a - b);
int curTime = 0;
int ans = 0;
for (int[] wo : wos) {
int endTime = wo[0];
int score = wo[1];
if (endTime >= curTime + 1) {
pq.offer(score);
ans += score;
curTime++;
} else {
if (pq.size() == 0) {
continue;
}
int min_score = pq.peek();
if (score > min_score) {
pq.poll();
pq.offer(score);
ans += score - min_score;
}
}
}
return ans;
}
}Python算法源码
import queue
# 输入获取
n = int(input())
wos = [list(map(int, input().split())) for i in range(n)]
# 算法入口
def getResult(wos):
# 按照SLA截止时间升序
wos.sort(key=lambda x: x[0])
pq = queue.PriorityQueue()
# ans 记录拿到的积分
ans = 0
# curTime 记录当前时间
curTime = 0
for wo in wos:
endTime, score = wo
if endTime >= curTime + 1:
pq.put(score)
ans += score
curTime += 1
else:
if pq.qsize() == 0:
continue
min_score = pq.queue[0]
if score > min_score:
pq.get()
pq.put(score)
ans += score - min_score
return ans
# 算法调用
print(getResult(wos))免责声明：
1、IT资源小站为非营利性网站，全站所有资料仅供网友个人学习使用，禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享，本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题，请立即告知本站，本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体，但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员，一律视为同意网站规定，本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0