题目描述
某部门开展Family Day开放日活动,其中有个从桶里取球的游戏,游戏规则如下:
有N个容量一样的小桶等距排开,
且每个小桶都默认装了数量不等的小球,
每个小桶装的小球数量记录在数组 bucketBallNums 中,
游戏开始时,要求所有桶的小球总数不能超过SUM,
如果小球总数超过SUM,则需对所有的小桶统一设置一个容量最大值 maxCapacity,
并需将超过容量最大值的小球拿出来,直至小桶里的小球数量小于 maxCapacity;
请您根据输入的数据,计算从每个小桶里拿出的小球数量。
限制规则一:
所有小桶的小球总和小于SUM,则无需设置容量值maxCapacity,并且无需从小桶中拿球出来,返回结果[]
限制规则二:
如果所有小桶的小球总和大于SUM,则需设置容量最大值maxCapacity,并且需从小桶中拿球出来,返回从每个小桶拿出的小球数量组成的数组;
输入描述
第一行输入2个正整数,数字之间使用空格隔开,其中第一个数字表示SUM,第二个数字表示bucketBallNums数组长度;
第二行输入N个正整数,数字之间使用空格隔开,表示bucketBallNums的每一项;
输出描述
找到一个maxCapacity,来保证取出尽量少的球,并返回从每个小桶拿出的小球数量组成的数组。
备注
- 1 ≤ bucketBallNums[i] ≤ 10^9
- 1 ≤ bucketBallNums.length = N ≤ 10^5
- 1 ≤ maxCapacity ≤ 10^9
- 1 ≤ SUM ≤ 10^9
用例
| 输入 | 14 7 2 3 2 5 5 1 4 |
| 输出 | [0,1,0,3,3,0,2] |
| 说明 | 小球总数为22,SUM=14,超出范围了,需从小桶取球, maxCapacity=1,取出球后,桶里剩余小球总和为7,远小于14 maxCapacity=2,取出球后,桶里剩余小球总和为13, maxCapacity=3,取出球后,桶里剩余小球总和为16,大于14 因此maxCapacity为2 ,每个小桶小球数量大于2的都需要拿出来; |
| 输入 | 3 3 1 2 3 |
| 输出 | [0,1,2] |
| 说明 | 小球总数为6,SUM=3,超出范围了,需从小桶中取球,maxCapacity=1,则小球总数为3,从1号桶取0个球,2号桶取1个球,3号桶取2个球; |
| 输入 | 6 2 3 2 |
| 输出 | [] |
| 说明 | 小球总数为5,SUM=6,在范围内,无需从小桶取球; |
题目解析
用例示意图如下:
由于所有桶中的球数之和超过了14,因此我们需要设置一个maxCapacity来限制每个桶中球的数量。
如果maxCapacity值设置为0,则所有桶中的球都需要取出,因此剩余球总数为0,小于sum=14,因此符合要求
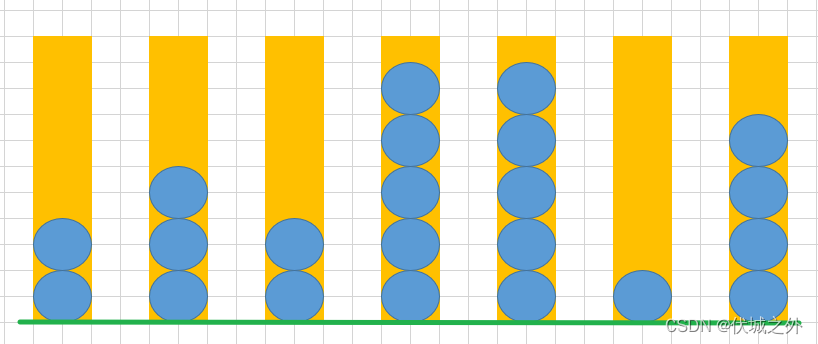
如果maxCapacity值设置为1,则所有桶中的球最多只保留1个,如下图所示,剩余球总数7个,也符合要求
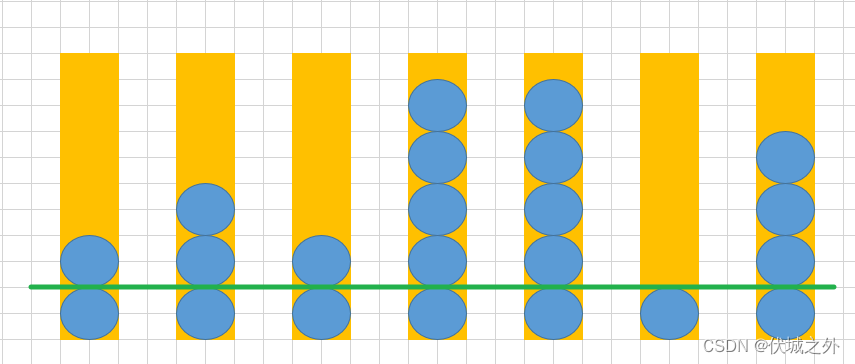
如果maxCapacity值设置为2,则所有桶中的球最多只保留2个,如下图所示,剩余球总数13个,也符合要求
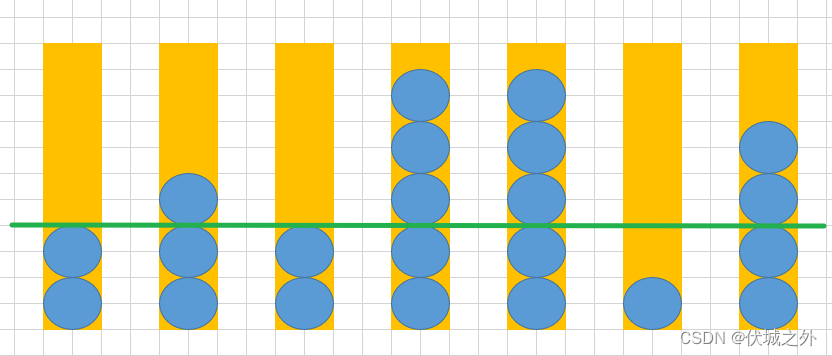
如果maxCapacity值设置为3,则所有桶中的球最多只保留3个,如下图所示,剩余球总数17个,不符合要求
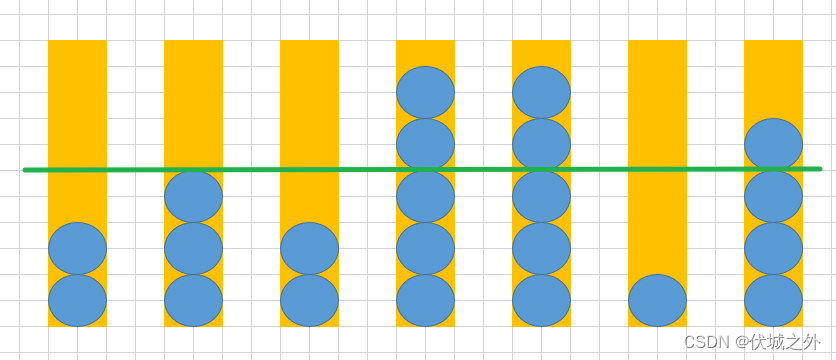
因此,我们可以发现,maxCapacity取值2时,剩余球数最多,总数量小于SUM=14,符合要求,且取出的球最少,分别为0,1,0,3,3,0,2。
那么我们是否需要从maxCapacity=0开始找呢?
答案是不需要,我们完全可以使用 SUM / bucketBallNums.length 求得一个最理想值.
比如用例中SUM=14,bucketBallNums.length=7,则每个桶中球数量的最理想值是14/7=2。
我们可以将此时最理想值作为maxCapacity的起始值。然后向后查找。
但是上面这种算法在应对较大数量级,可能会超时,因此改进策略是使用二分查找,具体逻辑请看
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
const [sum, n] = lines[0].split(" ").map(Number);
const arr = lines[1].split(" ").map(Number);
console.log(getResult(sum, arr, n));
lines.length = 0;
}
});
function getResult(sum, arr, n) {
const total = arr.reduce((p, c) => p + c);
if (total <= sum) return "[]";
let max_maxCapacity = Math.max.apply(null, arr);
let min_maxCapacity = Math.floor(sum / n);
// ans保存题解,初始题解为min_maxCapacity对应的题解
let ans = arr.map((count) =>
count > min_maxCapacity ? count - min_maxCapacity : 0
);
while (max_maxCapacity - min_maxCapacity > 1) {
const maxCapacity = Math.floor((max_maxCapacity + min_maxCapacity) / 2);
let remain = total;
// tmp数组保存的是每个桶移除的球的数量
const tmp = arr.map((count) => {
// r是每个桶需要移除的球的个数,如果桶内球数超过maxCapacity,则需要移除超出部分,否则不需要移除
const r = count > maxCapacity ? count - maxCapacity : 0;
remain -= r;
return r;
});
if (remain > sum) {
max_maxCapacity = maxCapacity;
} else if (remain < sum) {
min_maxCapacity = maxCapacity;
ans = tmp;
} else {
ans = tmp;
break;
}
}
return JSON.stringify(ans);
}
Java算法源码
考虑total会超过int范围,所以total设置为long类型。以及remain也设置为long类型。
import java.util.Arrays;
import java.util.Scanner;
import java.util.StringJoiner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int sum = sc.nextInt();
int n = sc.nextInt();
Integer[] arr = new Integer[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
System.out.println(getResult(sum, arr, n));
}
public static String getResult(int sum, Integer[] arr, int n) {
long total = 0;
int max_maxCapacity = 0;
for (int i = 0; i < n; i++) {
max_maxCapacity = Math.max(max_maxCapacity, arr[i]);
total += arr[i];
}
if (total <= sum) return "[]";
int min_maxCapacity = sum / n;
final int min_maxCapacity_copy = min_maxCapacity;
Integer[] ans =
Arrays.stream(arr)
.map(count -> count > min_maxCapacity_copy ? count - min_maxCapacity_copy : 0)
.toArray(Integer[]::new);
while (max_maxCapacity - min_maxCapacity > 1) {
int maxCapacity = (max_maxCapacity + min_maxCapacity) / 2;
// tmp数组保存的是每个桶移除的球的数量
Integer[] tmp = new Integer[n];
long remain = total;
for (int i = 0; i < arr.length; i++) {
// r是每个桶需要移除的球的个数,如果桶内球数超过maxCapacity,则需要移除超出部分,否则不需要移除
int r = arr[i] > maxCapacity ? arr[i] - maxCapacity : 0;
remain -= r;
tmp[i] = r;
}
if (remain > sum) {
max_maxCapacity = maxCapacity;
} else if (remain < sum) {
min_maxCapacity = maxCapacity;
ans = tmp;
} else {
ans = tmp;
break;
}
}
StringJoiner sj = new StringJoiner(",", "[", "]");
for (Integer an : ans) {
sj.add(an + "");
}
return sj.toString();
}
}
Python算法源码
# 输入获取
sumV, n = map(int, input().split())
arr = list(map(int, input().split()))
# 算法入口
def getResult(sumV, arr, n):
total = sum(arr)
if total <= sumV:
return "[]"
max_maxCapacity = max(arr)
min_maxCapacity = int(sumV / n)
# ans保存题解,初始题解为min_maxCapacity对应的题解
ans = list(map(lambda count: count - min_maxCapacity if count > min_maxCapacity else 0, arr))
while max_maxCapacity - min_maxCapacity > 1:
maxCapacity = int((max_maxCapacity + min_maxCapacity) / 2)
# tmp数组保存的是每个桶移除的球的数量
tmp = list(map(lambda count: count - maxCapacity if count > maxCapacity else 0, arr))
remain = total - sum(tmp)
if remain > sumV:
max_maxCapacity = maxCapacity
elif remain < sumV:
min_maxCapacity = maxCapacity
ans = tmp
else:
ans = tmp
break
return "[" + ",".join(map(str, ans)) + "]"
# 调用算法
print(getResult(sumV, arr, n))
免责声明:
评论0