题目描述
当前IT部门支撑了子公司颗粒化业务,该部门需要实现为子公司快速开租建站的能力,建站是指在一个全新的环境部署一套IT服务。
- 每个站点开站会由一系列部署任务项构成,每个任务项部署完成时间都是固定和相等的,设为1。
- 部署任务项之间可能存在依赖,假如任务2依赖任务1,那么等任务1部署完,任务2才能部署。
- 任务有多个依赖任务则需要等所有依赖任务都部署完该任务才能部署。
- 没有依赖的任务可以并行部署,优秀的员工们会做到完全并行无等待的部署。
给定一个站点部署任务项和它们之间的依赖关系,请给出一个站点的最短开站时间。
输入描述
第一行是任务数taskNum,第二行是任务的依赖关系数relationsNum
接下来 relationsNum 行,每行包含两个id,描述一个依赖关系,格式为:IDi IDj,表示部署任务i部署完成了,部署任务j才能部署,IDi 和 IDj 值的范围为:[0, taskNum)
注:输入保证部署任务之间的依赖不会存在环。
输出描述
一个整数,表示一个站点的最短开站时间。
备注
- 1 < taskNum ≤ 100
- 1 ≤ relationsNum ≤ 5000
用例
| 输入 | 5 5 0 4 1 2 1 3 2 3 2 4 |
| 输出 | 3 |
| 说明 |
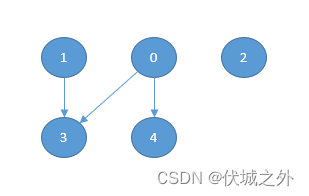
有5个部署任务项,5个依赖关系,如下图所示。
我们可以先同时部署任务项0和任务项1,然后部署任务项2,最后同时部署任务型3和任务型4.最短开战时间为3。 |
| 输入 | 5 3 0 3 0 4 1 3 |
| 输出 | 2 |
| 说明 |
有5个部署任务项,3个依赖关系,如下图所示。
我们可以先同时部署任务型0,任务型1,任务项2。然后再同时部署任务型4.最短开站时间为2。 |
题目解析
本题是经典的拓扑排序问题。因为题目种各任务之间有较为明显的前后依赖关系。
对于拓扑排序,我们可以看下面博客的解析:
华为OD机试 – 跳格子游戏_伏城之外的博客-CSDN博客_跳格子 华为机试
本题要求的并非是让我们判断拓扑结构中是否有环结构,因为题目已经说明了
输入保证部署任务之间的依赖不会存在环
本题是要我们求解最短开战时间,这里最短开战时间其实就是剥离入度0点的次数,如下图所示:
用例1中各顶点的入度值已用红色值标出
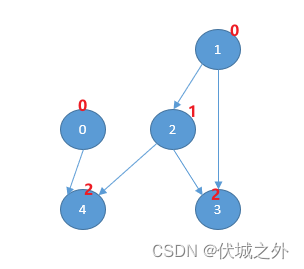
我们可以不断地剥离入度为0地顶点,因为题目说:
没有依赖的任务可以并行部署,优秀的员工们会做到完全并行无等待的部署。

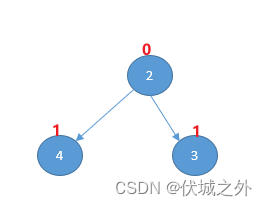
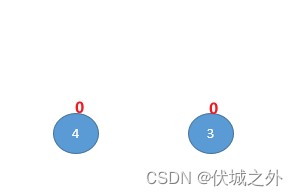
可以只需要剥离三次,而这也是最短建站时间。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let taskNum, relationsNum;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
taskNum = lines[0] - 0;
relationsNum = lines[1] - 0;
}
if (relationsNum && lines.length === relationsNum + 2) {
const relations = lines.slice(2).map((line) => line.split(" ").map(Number));
console.log(getResult(relations, taskNum));
lines.length = 0;
}
});
function getResult(relations, taskNum) {
const next = {};
const inDegree = new Array(taskNum).fill(0);
for (let relation of relations) {
const [a, b] = relation; // a → b
next[a] ? next[a].push(b) : (next[a] = [b]); // a的下一个顶点有b
inDegree[b]++; // b顶点的入度++
}
const queue = [];
let t = 1;
for (let i = 0; i < taskNum; i++) {
if (inDegree[i] === 0) {
queue.push([i, t]); // i含义是入度为0的顶点,t含义是该顶点所处建站时间
}
}
while (queue.length) {
const [task, time] = queue.shift(); // 注意这里为了维持t,一定要使用队列先进先出,出队代表删除某顶点
next[task]?.forEach((nxt) => {
// 该顶点被删除,则其后继点的入度值--,若--后入度为0,则将成为新的出队点
if (--inDegree[nxt] === 0) {
t = time + 1; // 此时建站时间+1
queue.push([nxt, t]);
}
});
}
return t;
}
Java算法源码
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int taskNum = sc.nextInt();
int relationsNum = sc.nextInt();
int[][] relations = new int[relationsNum][2];
for (int i = 0; i < relationsNum; i++) {
relations[i][0] = sc.nextInt();
relations[i][1] = sc.nextInt();
}
System.out.println(getResult(relations, taskNum));
}
public static int getResult(int[][] relations, int taskNum) {
HashMap<Integer, ArrayList<Integer>> next = new HashMap<>();
int[] inDegree = new int[taskNum];
for (int[] relation : relations) {
int a = relation[0];
int b = relation[1];
next.putIfAbsent(a, new ArrayList<>());
next.get(a).add(b); // a的下一个顶点有b
inDegree[b]++; // b顶点的入度++
}
LinkedList<Integer[]> queue = new LinkedList<>();
int t = 1;
for (int i = 0; i < taskNum; i++) {
if (inDegree[i] == 0) {
queue.add(new Integer[] {i, t}); // i含义是入度为0的顶点,t含义是该顶点所处建站时间
}
}
while (queue.size() > 0) {
Integer[] tmp = queue.removeFirst(); // 注意这里为了维持t,一定要使用队列先进先出,出队代表删除某顶点
int task = tmp[0];
int time = tmp[1];
if (next.containsKey(task) && next.get(task).size() > 0) {
for (Integer nxt : next.get(task)) {
// 该顶点被删除,则其后继点的入度值--,若--后入度为0,则将成为新的出队点
if (--inDegree[nxt] == 0) {
t = time + 1; // 此时建站时间+1
queue.add(new Integer[] {nxt, t});
}
}
}
}
return t;
}
}
Python算法源码
taskNum = int(input())
relationsNum = int(input())
relations = []
for i in range(relationsNum):
relations.append(list(map(int, input().split())))
next = {}
inDegree = [0 for i in range(taskNum)]
for relation in relations:
a, b = relation
# a的下一个顶点有b
if next.get(a) is None:
next[a] = [b]
else:
next[a].append(b)
# b顶点的入度++
inDegree[b] += 1
queue = []
t = 1
for i in range(taskNum):
if inDegree[i] == 0:
queue.append((i, t)) # i含义是入度为0的顶点,t含义是该顶点所处建站时间
while len(queue) > 0:
task, time = queue.pop(0) # 注意这里为了维持t,一定要使用队列先进先出,出队代表删除某顶点
if next.get(task) is not None and len(next[task]) > 0:
for nxt in next[task]:
# 该顶点被删除,则其后继点的入度值--,若--后入度为0,则将成为新的出队点
inDegree[nxt] -= 1
if inDegree[nxt] == 0:
t = time + 1 # 此时建站时间+1
queue.append((nxt, t))
print(t)
免责声明:
1、IT资源小站为非营利性网站,全站所有资料仅供网友个人学习使用,禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享,本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题,请立即告知本站,本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体,但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员,一律视为同意网站规定,本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0