题目描述
给一个无向图染色,可以填红黑两种颜色,必须保证相邻两个节点不能同时为红色,输出有多少种不同的染色方案?
输入描述
第一行输入M(图中节点数) N(边数)
后续N行格式为:V1 V2表示一个V1到V2的边。
数据范围:1 <= M <= 15,0 <= N <= M * 3,不能保证所有节点都是连通的。
输出描述
输出一个数字表示染色方案的个数。
用例
| 输入 | 4 4 1 2 2 4 3 4 1 3 |
| 输出 | 7 |
| 说明 |
4个节点,4条边,1号节点和2号节点相连, 2号节点和4号节点相连,3号节点和4号节点相连, 1号节点和3号节点相连, 若想必须保证相邻两个节点不能同时为红色,总共7种方案。 |
| 输入 | 3 3 1 2 1 3 2 3 |
| 输出 | 4 |
| 说明 | 无 |
| 输入 | 4 3 1 2 2 3 3 4 |
| 输出 | 8 |
| 说明 | 无 |
| 输入 | 4 3 1 2 1 3 2 3 |
| 输出 | 8 |
| 说明 | 无 |
题目解析
2022.12.25 更正解析说明,感谢Andy___Zhong指出错误。
本题其实就是求解连通图的染色方案,
目前我想到的最好方式是暴力法,即通过回溯算法,求解出染红节点的全组合,
n个数的全组合数量一共有 (2^n) – 1。
比如:1,2,3的全组合情况有:1、2、3、12、13、23、123,即 (2^3) – 1 = 7个。
本题中节点一共有m个,而1 <= m <= 15,即最多有 (2^15) – 1 = 32767 个组合情况,这个数量级不算多。 因此暴力法可行。
我们需要尝试对组合中的节点进行染红色,但是相邻节点不能同时染成红色。因此,在求解全组合时,还可以进行剪枝优化,即判断新加入的节点 是否和 已存在的节点相邻,如果相邻,则剪枝,如果不相邻则继续递归。
// 连通图的染色方案数求解
function getDyeCount(arr, m) {
// connect用于存放每个节点的相邻节点
const connect = {};
for (let [v1, v2] of arr) {
connect[v1] ? connect[v1].add(v2) : (connect[v1] = new Set([v2]));
connect[v2] ? connect[v2].add(v1) : (connect[v2] = new Set([v1]));
}
// 必有一种全黑的染色方案
let count = 1;
// 求解染红节点的全组合情况
function dfs(m, index, path) {
if (path.length === m) return;
outer: for (let i = index; i <= m; i++) {
// 如果新加入节点和已有节点相邻,则说明新加入节点不能染成红色,需要进行剪枝
for (let j = 0; j < path.length; j++) {
if (path[j].has(i)) continue outer;
}
count++;
path.push(connect[i]);
dfs(m, i + 1, path);
path.pop();
}
}
// 节点从1开始
dfs(m, 1, []);
return count;
}本题,到此还未结束,因为题目中有一句话:
不能保证所有节点都是连通的
这说明什么呢?即对应用例4的情况,用例4对应的无向图如下:
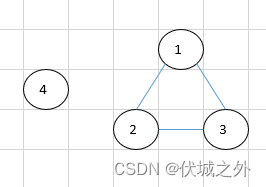
此时一共有8种染色方案如下:
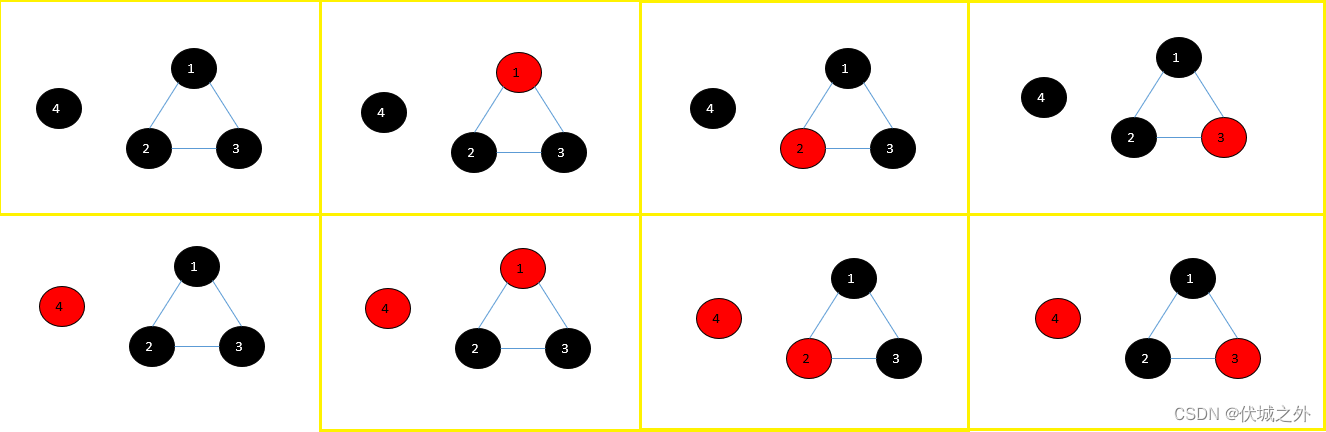
其实就是先求解无向图的各个连通分量,比如用例4的无向图就有两个连通分量,分别是:
- {4}
- {1,2,3}
然后求解各连通分量各自的染色方案,比如
- {4} 有2种染色方案
- {1,2,3} 有4种染色方案
那么总染色方案数目就是2*4=8种
因此,本题还考察了连通分量的求解。
连通分量的求解可以使用并查集,关于并查集知识请看:
但是本题实现上可以取巧,即不需要使用并查集去求解连通分量,而是完全依赖于暴力,因为不管节点是否在一个连通分量中,还是不在一个连通分量中,他们的染色都要满足:
相邻节点不能同时为红色
因此,处于两个连通分量中的节点必然不相连,则必然可以同时染红,因此直接用前面求染红节点组合就可以,不需要用并查集。
补充一个边界用例情况:
4 3
2 3
2 4
3 4
输出应该是8
但是节点1和任何其他节点不相连,也没有在边,因此下面代码,统计connect时,即统计每个节点的相邻节点,必然统计不到节点1,即connect[1] 的值为null,因此后续获取节点1的相邻节点时会得到null,此时我们应该要特殊处理null。
JavaScript算法源码
直接利用节点间相邻关系暴力枚举所有染色方案。该方案实现上更简单,但是性能没有基于并查集求出各连通分量后分别求解染色方案的好。
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let m, n;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
[m, n] = lines[0].split(" ").map(Number);
}
if (n !== undefined && lines.length === n + 1) {
const arr = lines.slice(1).map((line) => line.split(" ").map(Number));
console.log(getResult(arr, m));
lines.length = 0;
}
});
/**
*
* @param {*} arr 边,即[v1, v2]
* @param {*} m 点数量
*/
function getResult(arr, m) {
// connect用于存放每个节点的相邻节点
const connect = {};
for (let [v1, v2] of arr) {
connect[v1] ? connect[v1].add(v2) : (connect[v1] = new Set([v2]));
connect[v2] ? connect[v2].add(v1) : (connect[v2] = new Set([v1]));
}
// 必有一种全黑的染色方案
let count = 1;
// 求解染红节点的全组合情况
function dfs(m, index, path) {
if (path.length === m) return;
outer: for (let i = index; i <= m; i++) {
// 如果新加入节点和已有节点相邻,则说明新加入节点不能染成红色,需要进行剪枝
for (let j = 0; j < path.length; j++) {
if (path[j].has(i)) continue outer;
}
count++;
if (connect[i] != undefined) {
path.push(connect[i]);
dfs(m, i + 1, path);
path.pop();
} else {
dfs(m, i + 1, path);
}
}
}
// 节点从1开始
dfs(m, 1, []);
return count;
}
Java算法源码
直接利用节点间相邻关系暴力枚举所有染色方案。该方案实现上更简单,但是性能没有基于并查集求出各连通分量后分别求解染色方案的好。
import java.util.HashMap;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int n = sc.nextInt();
int[][] edges = new int[n][2];
for (int i = 0; i < n; i++) {
edges[i][0] = sc.nextInt();
edges[i][1] = sc.nextInt();
}
System.out.println(getResult(edges, m));
}
/**
* @param edges 边,即[v1, v2]
* @param m 点数量
* @return
*/
public static int getResult(int[][] edges, int m) {
// connect用于存放每个节点的相邻节点
HashMap<Integer, HashSet<Integer>> connect = new HashMap<>();
for (int[] edge : edges) {
connect.putIfAbsent(edge[0], new HashSet<>());
connect.get(edge[0]).add(edge[1]);
connect.putIfAbsent(edge[1], new HashSet<>());
connect.get(edge[1]).add(edge[0]);
}
// 节点从index=1开始,必有count=1个的全黑染色方案
return dfs(connect, m, 1, 1, new LinkedList<>());
}
// 该方法用于求解给定多个节点染红的全组合数
public static int dfs(
HashMap<Integer, HashSet<Integer>> connect,
int m,
int index,
int count,
LinkedList<HashSet<Integer>> path) {
if (path.size() == m) return count;
outer:
for (int i = index; i <= m; i++) {
// 如果新加入节点i和已有节点j相邻,则说明新加入节点不能染成红色,需要进行剪枝
for (HashSet<Integer> p : path) {
if (p.contains(i)) continue outer;
}
count++;
if (connect.containsKey(i)) {
path.addLast(connect.get(i));
count = dfs(connect, m, i + 1, count, path);
path.removeLast();
} else {
count = dfs(connect, m, i + 1, count, path);
}
}
return count;
}
}
Python算法源码
# 输入获取
m, n = map(int, input().split())
arr = [list(map(int, input().split())) for i in range(n)]
# 算法入口
def getResult(arr, m):
"""
:param arr: 边,即[v1, v2]
:param m: 点数量
:return: 染色方案数
"""
# connect用于存放每个节点的相邻节点
connect = {}
for v1, v2 in arr:
if connect.get(v1) is None:
connect[v1] = set()
connect[v1].add(v2)
if connect.get(v2) is None:
connect[v2] = set()
connect[v2].add(v1)
# 节点从1开始
return dfs(m, 1, [], 1, connect)
# 求解染红节点的全组合情况
def dfs(m, index, path, count, connect):
"""
:param m: 点数量,点从1计数
:param index: 当前第几个点
:param path: 保存点的容器
:param count: 染色方案数量
:param connect: 每个节点的相邻节点
:return: 染色方案数量
"""
if len(path) == m:
return count
flag = False
for i in range(index, m + 1):
# 如果新加入节点和已有节点相邻,则说明新加入节点不能染成红色,需要进行剪枝
for p in path:
if i in p:
flag = True
break
if flag:
flag = False
continue
count += 1
if connect.get(i) is not None:
path.append(connect.get(i))
count = dfs(m, i + 1, path, count, connect)
path.pop()
else:
count = dfs(m, i + 1, path, count, connect)
return count
# 算法调用
print(getResult(arr, m))免责声明:
评论0