题目描述
高铁城市圈对人们的出行、经济的拉动效果明显。每年都会规划新的高铁城市圈建设。
在给定城市数量、可建设高铁的两城市间的修建成本列表、以及结合城市商业价值会固定建设的两城市建高铁。
请你设计算法,达到修建城市高铁的最低成本。注意,需要满足城市圈内城市间两两互联可达(通过其他城市中转可达也属于满足条件)。
输入描述
输入信息包括:
- 第一行,包含此城市圈中城市的数量、可建设高铁的两城市间修建成本列表数量、必建高铁的城市列表。三个数字用空格间隔。
- 可建设高铁的两城市间的修建成本列表,为多行输入数据,格式为3个数字,用空格分隔,长度不超过1000。
- 固定要修建的高铁城市列表,是上面参数2的子集,可能为多行,每行输入为2个数字,以空格分隔。
城市id从1开始编号,建设成本的取值为正整数,取值范围均不会超过1000
输出描述
修建城市圈高铁的最低成本,正整数。如果城市圈内存在两城市之间无法互联,则返回-1。
用例
| 输入 | 3 3 0 1 2 10 1 3 100 2 3 50 |
| 输出 | 60 |
| 说明 | 3 3 0城市圈数量为3,表示城市id分别为1,2,3 1 2 10城市1,2间的高铁修建成本为10 1 3 100城市1,3间的高铁修建成本为100 2 3 50城市2,3间的高铁修建成本为50 满足修建成本最低,只需要建设城市1,2间,城市2,3间的高铁即可,城市1,3之间可通过城市2中转来互联。这样最低修建成本就是60。 |
| 输入 | 3 3 1 1 2 10 1 3 100 2 3 50 1 3 |
| 输出 | 110 |
| 说明 |
3 3 1 城市圈数量为3,表示城市id分别为1,2,3 1 2 10 城市1,2间的高铁修建成本为10 1 3 100 城市1,3间的高铁修建成本为100 2 3 50 城市2,3间的高铁修建成本为50 1 3 城市1,3间的高铁必须修建 因为城市1,3间的高铁必须修建,在满足互联的条件下,再增加修建城市1,2间的高铁即可,最低成本为110 |
题目解析
本题是求解最小生成树的变种题。
在了解最小生成树概念前,我们需要先了解生成树的概念:
在无向连通图中,生成树是指包含了全部顶点的极小连通子图。
生成树包含原图全部的n个顶点和n-1条边。(注意,边的数量一定是n-1)
比如下面无向连通图例子:
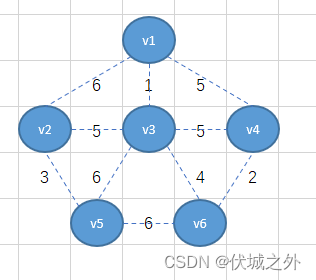
根据生成树概念,我们可以基于上面无向连通图,产生多个生成树,下面举几个生成树例子:
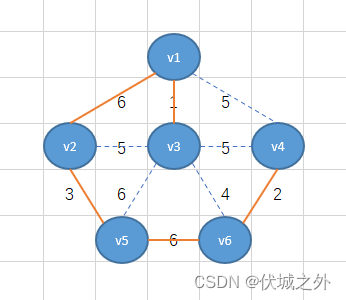
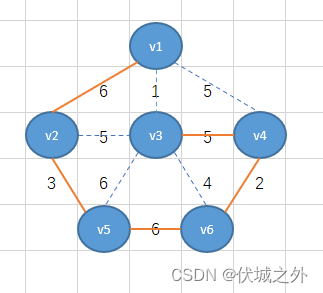
如上图我们用n-1条橙色边连接了n个顶点。这样就从无向连通图中产生了生成树。
为什么生成树只能由n-1条边呢?
因为少一条边,则生成树就无法包含所有顶点。多一条边,则生成树就会形成环。
而生成树最重要的两个特性就是:
1、包含所有顶点
2、无环
了解了生成树概念后,我们就可以进一步学习最小生成树了。
我们回头看看无向连通图,可以发现每条边都有权重值,比如v1-v2权重值是6,v3-v6权重值是4。
最小生成树指的是,生成树中n-1条边的权重值之和最小。
那么如何才能准确的找出一个无向连通图的最小生成树呢?
有两种算法:Prim算法和Kruskal算法。
Prim算法是基于顶点找最小生成树。Kruskal是基于边找最小生成树。
首先,我们介绍Prim算法:
我们可以选择无向连通图中的任意一个顶点作为起始点,比如我们选v1顶点为起始点
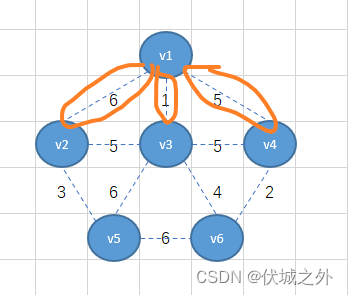
从v1顶点出发,有三条边,我们选择权重最小的1,即将v1-v3相连
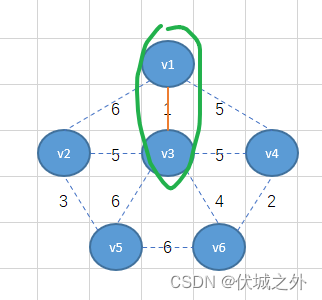
此时我们需要将v1-v3看成一个整体,然后继续找这个整体出发的所有边里面的最小的,
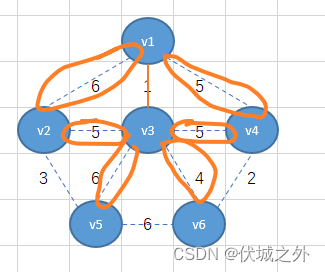
可以发现为最小权重为4,因此,将v3-v6相连
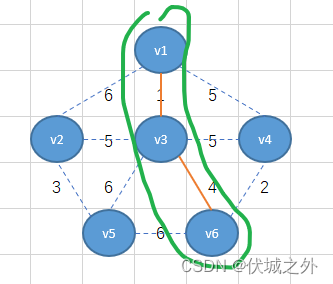
接着将v1-v3-v6看出一个整体,找这个整体出发的所有边里面的最小的,可以找到最小权重2,因此将v6-v4相连
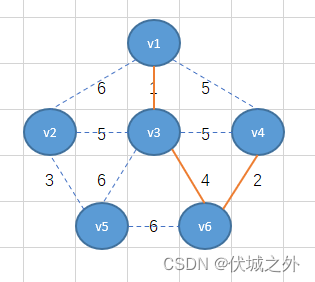
但是接下来,我们会发现,从v1-v3-v6-v4整体出发的所有边里面同时有三个最小权重5,那么该如何选择呢?
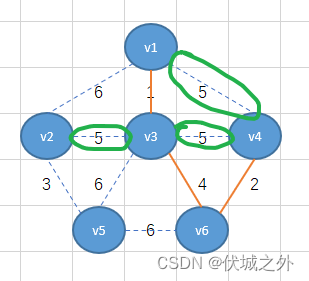
其实不难看出,如果选择v4-v3,或者v4-v1相连,则对应的生成树就形成了环结构,因此就不符合生成树特性了,因此我们只能选择v3-v2。
(注意:如果有多个相同的最小权重边可选,并且都不会产生环结构,则可以选择其中任意一条边,最终得到结果都是最小生成树)
其实,不仅仅在上面遇到相同权重边时,需要判断是否形成环,在前选择每一条边时都需要判断是否形成环,一旦选择的边能够形成环,那么我们就应该舍弃它,选择第二小的权重边,并继续判断。
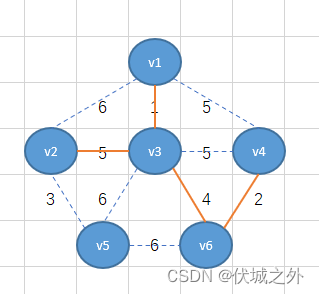
按照上面逻辑,我们可以继续找到v1-v2-v3-v4-v6整体出发所有边中的最小权重边3,即将v2-v5相连,并且连接后不会形成环
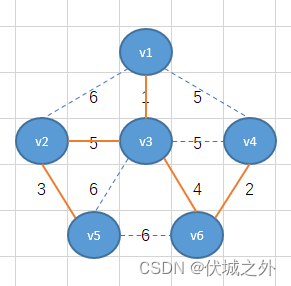
此时选择的边数已经达到了n-1条,因此可以结束逻辑,而现在得到的就是最小生成树。我们可以将这个最小生成数的所有边的权重值之和计算出来为20。
上面这种基于顶点的找最小生成树的方式就是Prim算法。
接下来介绍Kruskal算法:
Kruskal算法要求我们将所有的边按照权重值升序排序,因此可得:
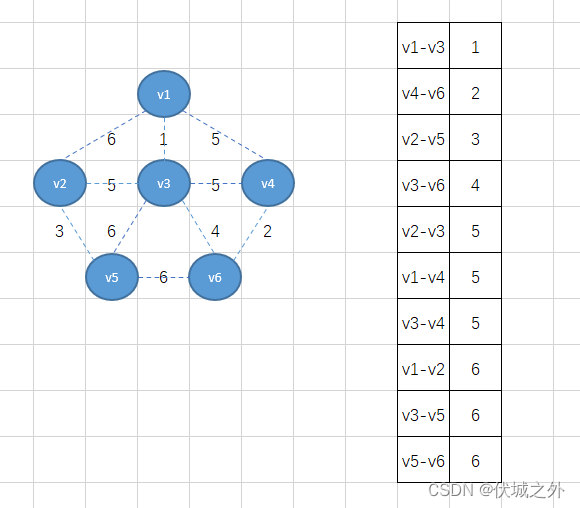
首先,我们将权重最小的边v1-v3加入,得到下图
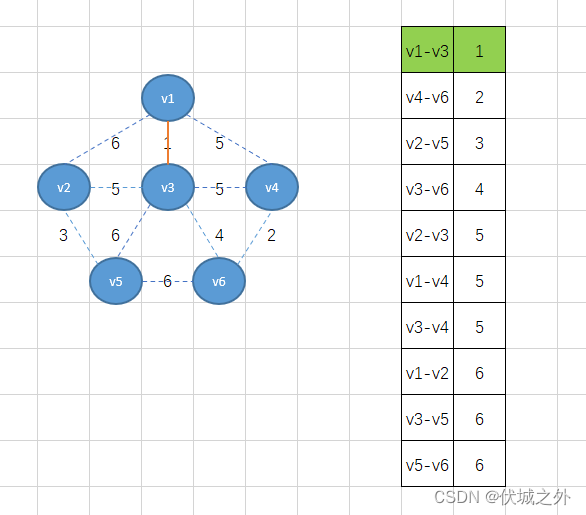
接着将下个最小权重2的边v4-v6加入
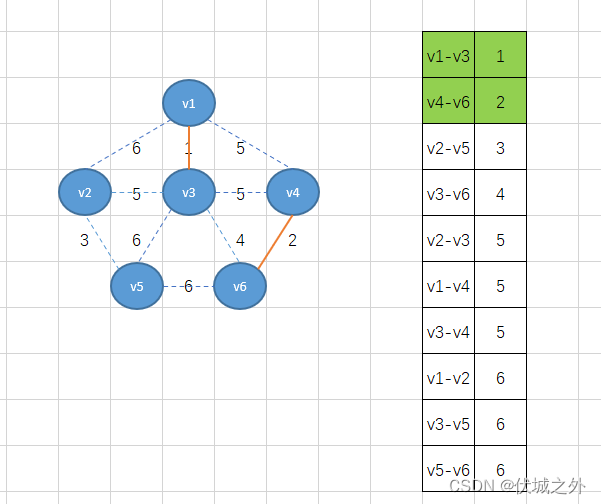
接着继续加最小权重边
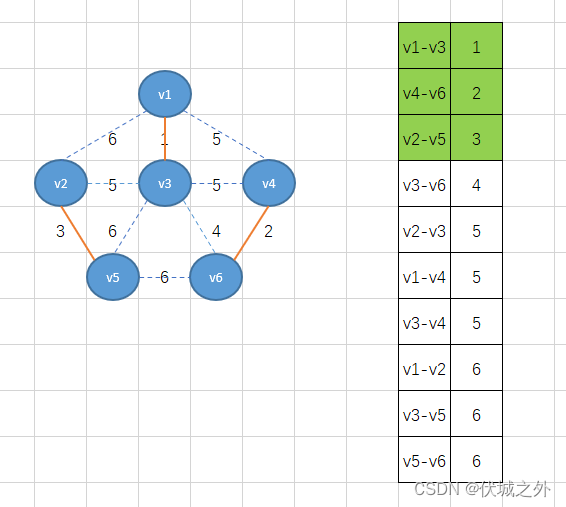
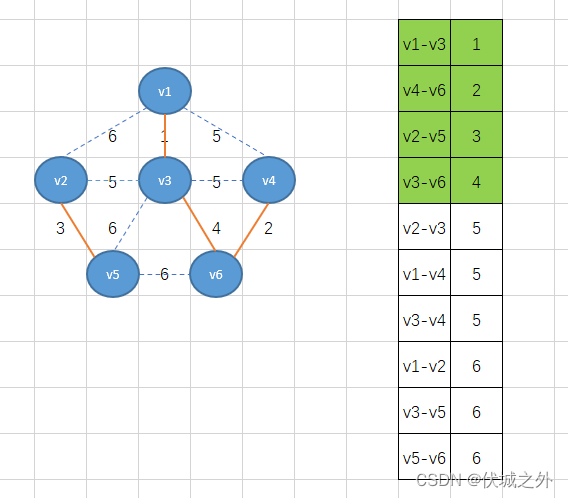
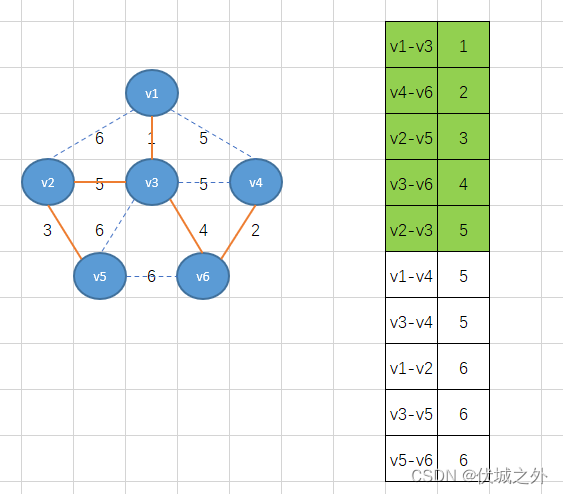
此时边数已经达到n-1,而刚好这个过程中也没有环的形成,因此得到的就是最小生成树。
但是这里有巧合因素在里面,因为最后一步中,最小权重5的边有多条,如果并不是v2-v3排在前面呢,比如是v1-v4呢?
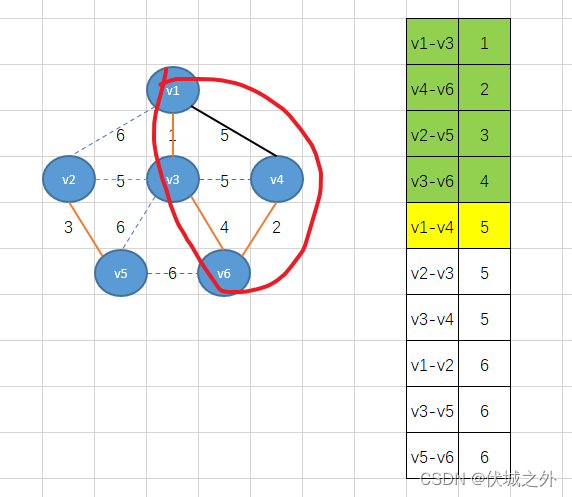
可以发现,形成了环,因此我们应该舍弃这条边,继续找剩下的最小权重边。最后总能找到v2-v3。
通过上面对于Prim算法和Kruskal算法的分析,我们发现一个关键点,那就是必须实时判断是否产生了环?
那么判断环的存在就是实现上面Prim算法和Kruskal算法的关键点!
其实,生成树就是一个连通分量,初始时,生成树这个连通分量只有一个顶点(Prim),或者两个顶点(Kruskal),后面会不断合入新的顶点进来,来扩大连通分量范围。
而连通分量可以使用并查集表示,
并查集本质就是一个长度为n的数组(n为无向图的顶点数),数组索引值代表图中某个顶点child,数组索引指向的元素值,代表child顶点的祖先顶点father。
初始时,每个child的father都是自己。即初始时,默认有n个连通分量。
比如 arr = [1,1,1,5,5,5] 数组就可以模拟出一个无向图
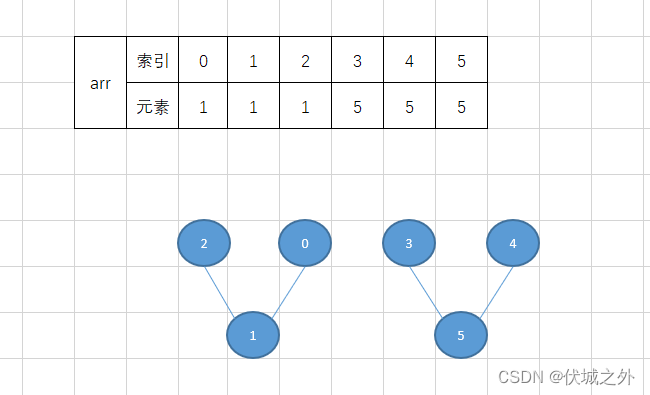
- 0顶点的祖先是1顶点 =》 arr[0] = 1
- 1顶点的祖先是1顶点 =》 arr[1] = 1
- 2顶点的祖先是1顶点 =》 arr[2] = 1
如果大家还不理解并查集结构,可以看
我们可以用father指代一个连通分量。比如上面arr = [1,1,1,5,5,5]就有两个连通分量,分别是father为1的连通分量和father为5的连通分量。
最小生成树中的顶点必然都处于同一个连通分量中,因此每加入一个新的顶点child_new,我们我们就可以看它的father是否已经是连通分量对应的father,如果是,则说明顶点child_new其实已经存在于最小生成树中了,因此就产生了环,比如下面例子:

我们定义一个数组arr,来表示并查集结构,初始时,
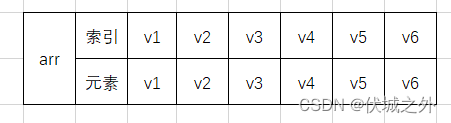
如果达到上图橙色边连接状态,则arr变为
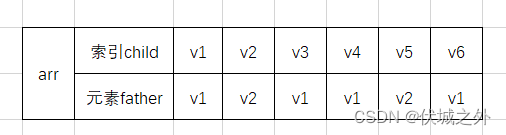
接下来加入黑色边,即v4顶点的father改成v1,但是实际上v4的father已经是v1,那么此时如果再强行加入的话,那么就形成了环。
下面,我们来解答本题:
本题要求的最低成本,其实就是最小生成树所有边相加得到的最小权重和。
但是本题,又不是一个纯粹的求最小生成树的题。
因为,本题中规定了一些“必建高铁的两个城市”,那么多个“必建高铁的两个城市”是非常有可能形成环的。
但是,我们并不需要纠结这个,因为我们要求的不是最小生成树,而是最小权重和,只是这个最小权重和中某些值已经固定了,这些固定的值就是“必建高铁的两个城市”对应的费用。
我们定义一个minFee来代表最低成本,首先我们需要将必建高铁的成本计算进去。并且在计算的过程中,将必建高铁的两个城市(两个顶点)纳入一个连通分量中(基于并查集)。
之后,我们在将 “可以建高铁” 的列表 按照成本费用升序排序(Kruskal算法),然后遍历排序后列表,依次将“可以建高铁” 的两个城市(两个顶点)尝试纳入连通分量中,如果有环,则不纳入,无环,则纳入,纳入的话,则将成本费用计入minFee中。
那么上面逻辑何时结束呢?1、所有顶点已经纳入到一个连通分量中;2、循环结束。
循环结束后,
如果并查集中的连通分量数量为1,则说明所有城市(顶点)已经通车,且是最低成本。此时返回minFee就是题解。
如果并查集中的连通分量数量不为1,则说明所有城市(顶点)无法连通,返回-1。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, can, must;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
[n, can, must] = lines[0].split(" ").map(Number);
}
if (
can !== undefined &&
must !== undefined &&
lines.length === can + must + 1
) {
lines.shift();
const cans = lines
.splice(0, can)
.map((line) => line.split(" ").map(Number));
const musts = lines.map((line) => line.split(" ").map(Number));
console.log(getResult(n, cans, musts));
lines.length = 0;
}
});
/**
*
* @param {*} n 一共几个城市
* @param {*} cans 哪些城市之间可以修建高铁,以及修建费用
* @param {*} musts 哪些城市之间必须修建高铁
*/
function getResult(n, cans, musts) {
const ufs = new UnionFindSet(n);
// 这里因为不知道题目用例输入的城市序号是否是按顺序的,因此需要排个序。
// 并且为了方便统计“必建高铁”的费用,我们需要将cans数组改造为对象,key为'1-2' 两个城市,val为 这两个城市建高铁的费用
const cansObj = {};
for (let [c1, c2, fee] of cans) {
const key = c1 < c2 ? `${c1}-${c2}` : `${c2}-${c1}`;
cansObj[key] = fee;
}
// must数组中元素也改造为'1-2' 两个城市字符串的形成,方便从cansObj中获取对应的费用
musts = musts.map((must) => {
const [c1, c2] = must;
return c1 < c2 ? `${c1}-${c2}` : `${c2}-${c1}`;
});
let minFee = 0;
for (let must of musts) {
// 计入必建高铁的费用到minFee中
minFee += cansObj[must];
const [c1, c2] = must.split("-").map(Number);
// 并将必建高铁的两个城市纳入同一个连通分量重
ufs.union(c1, c2);
}
// 如果必建高铁本身已经满足所有城市通车了,那么直接返回minFee
if (ufs.count === 1) return minFee;
// 否则,按照求解最小生成树的Kruskal算法,将高铁线(即图的边)按照成本费用(即边的权重)升序
cans.sort((a, b) => a[2] - b[2]);
// 遍历排序后的cans,每次得到的都是当前的最小权重边
for (let [c1, c2, fee] of cans) {
// 如果对应城市已经接入高铁线(即处于连通分量中)则再次合入就会产生环,因此不能合入,否则就可以合入
// if (ufs.fa[c1] !== ufs.fa[c2]) {
if (ufs.find(c1) !== ufs.find(c2)) {
ufs.union(c1, c2);
// 若可以合入,则将对应的建造成本计入minFee
minFee += fee;
}
// 如果此时,所有城市都通车了(即并查集中只有一个连通分量),则提前结束循环
if (ufs.count === 1) break;
}
// 如果循环完,发现并查集中还有多个连通分量,那么代表有的城市无法通车,因此返回-1
if (ufs.count > 1) return -1;
return minFee;
}
// 并查集
class UnionFindSet {
constructor(n) {
this.fa = new Array(n + 1).fill(0).map((_, i) => i);
this.count = n;
}
find(x) {
if (x !== this.fa[x]) {
return (this.fa[x] = this.find(this.fa[x]));
}
return x;
}
union(x, y) {
const x_fa = this.find(x);
const y_fa = this.find(y);
if (x_fa !== y_fa) {
this.fa[y_fa] = x_fa;
this.count--;
}
}
}
Java算法源码
import java.util.Arrays;
import java.util.HashMap;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int can = sc.nextInt();
int must = sc.nextInt();
int[][] cans = new int[can][3];
for (int i = 0; i < can; i++) {
cans[i][0] = sc.nextInt();
cans[i][1] = sc.nextInt();
cans[i][2] = sc.nextInt();
}
int[][] musts = new int[must][2];
for (int i = 0; i < must; i++) {
musts[i][0] = sc.nextInt();
musts[i][1] = sc.nextInt();
}
System.out.println(getResult(n, cans, musts));
}
/**
* @param n 一共几个城市
* @param cans 哪些城市之间可以修建高铁,以及修建费用
* @param musts 哪些城市之间必须修建高铁
* @return 最少费用
*/
public static int getResult(int n, int[][] cans, int[][] musts) {
UnionFindSet ufs = new UnionFindSet(n);
// 为了方便统计“必建高铁”的费用,我们需要将cans数组改造为cansMap,key为'1-2' 两个城市,val为 这两个城市建高铁的费用
HashMap<String, Integer> cansMap = new HashMap<>();
for (int[] can : cans) {
int city1 = can[0], city2 = can[1], fee = can[2];
String key = city1 < city2 ? city1 + "-" + city2 : city2 + "-" + city1;
cansMap.put(key, fee);
}
int minFee = 0;
for (int[] must : musts) {
// 计入必建高铁的费用到minFee中
String key = must[0] < must[1] ? must[0] + "-" + must[1] : must[1] + "-" + must[0];
minFee += cansMap.get(key);
// 并将必建高铁的两个城市纳入同一个连通分量重
ufs.union(must[0], must[1]);
}
// 如果必建高铁本身已经满足所有城市通车了,那么直接返回minFee
if (ufs.count == 1) return minFee;
// 否则,按照求解最小生成树的Kruskal算法,将高铁线(即图的边)按照成本费用(即边的权重)升序
Arrays.sort(cans, (a, b) -> a[2] - b[2]);
// 遍历排序后的cans,每次得到的都是当前的最小权重边
for (int[] can : cans) {
int city1 = can[0], city2 = can[1], fee = can[2];
// 如果对应城市已经接入高铁线(即处于连通分量中)则再次合入就会产生环,因此不能合入,否则就可以合入
// if (ufs.fa[city1] != ufs.fa[city2]) {
if (ufs.find(city1) != ufs.find(city2)) {
ufs.union(city1, city2);
// 若可以合入,则将对应的建造成本计入minFee
minFee += fee;
}
// 如果此时,所有城市都通车了(即并查集中只有一个连通分量),则提前结束循环
if (ufs.count == 1) break;
}
// 如果循环完,发现并查集中还有多个连通分量,那么代表有的城市无法通车,因此返回-1
if (ufs.count > 1) return -1;
return minFee;
}
}
// 并查集
class UnionFindSet {
int[] fa;
int count;
public UnionFindSet(int n) {
this.fa = new int[n + 1];
this.count = n;
for (int i = 0; i < n + 1; i++) this.fa[i] = i;
}
public int find(int x) {
if (x != this.fa[x]) {
return (this.fa[x] = this.find(this.fa[x]));
}
return x;
}
public void union(int x, int y) {
int x_fa = this.find(x);
int y_fa = this.find(y);
if (x_fa != y_fa) {
this.fa[y_fa] = x_fa;
this.count--;
}
}
}
Python算法源码
# 并差集
class UnionFindSet:
def __init__(self, n):
self.fa = [i for i in range(n + 1)]
self.count = n
def find(self, x):
if x != self.fa[x]:
self.fa[x] = self.find(self.fa[x])
return self.fa[x]
return x
def union(self, x, y):
x_fa = self.find(x)
y_fa = self.find(y)
if x_fa != y_fa:
self.fa[y_fa] = x_fa
self.count -= 1
# 算法入口
def getResult(n, cans, musts):
"""
:param n: 一共几个城市
:param cans: 哪些城市之间可以修建高铁,以及修建费用
:param musts: 哪些城市之间必须修建高铁
:return: 修建城市高铁的最低成本
"""
ufs = UnionFindSet(n)
# 这里因为不知道题目用例输入的城市序号是否是按顺序的,因此需要排个序。
# 并且为了方便统计“必建高铁”的费用,我们需要将cans数组改造为对象,key为'1-2' 两个城市,val为 这两个城市建高铁的费用
canDict = {}
for c1, c2, fee in cans:
key = f"{c1}-{c2}" if c1 < c2 else f"{c2}-{c1}"
canDict[key] = fee
# must数组中元素也改造为'1-2' 两个城市字符串的形成,方便从cansObj中获取对应的费用
musts = map(lambda must: f"-" if must[0] < must[1] else f"-", musts)
minFee = 0
for must in musts:
# 计入必建高铁的费用到minFee中
minFee += canDict[must]
c1, c2 = map(int, must.split("-"))
# 并将必建高铁的两个城市纳入同一个连通分量重
ufs.union(c1, c2)
# 如果必建高铁本身已经满足所有城市通车了,那么直接返回minFee
if ufs.count == 1:
return minFee
# 否则,按照求解最小生成树的Kruskal算法,将高铁线(即图的边)按照成本费用(即边的权重)升序
cans.sort(key=lambda x: x[2])
# 遍历排序后的cans,每次得到的都是当前的最小权重边
for c1, c2, fee in cans:
# 如果对应城市已经接入高铁线(即处于连通分量中)则再次合入就会产生环,因此不能合入,否则就可以合入
# if ufs.fa[c1] != ufs.fa[c2]:
if ufs.find(c1) != ufs.find(c2):
ufs.union(c1, c2)
# 若可以合入,则将对应的建造成本计入minFee
minFee += fee
# 如果此时,所有城市都通车了(即并查集中只有一个连通分量),则提前结束循环
if ufs.count == 1:
break
# 如果循环完,发现并查集中还有多个连通分量,那么代表有的城市无法通车,因此返回-1
if ufs.count > 1:
return -1
return minFee
# 输入获取
n, can, must = map(int, input().split())
cans = [list(map(int, input().split())) for i in range(can)]
musts = [list(map(int, input().split())) for i in range(must)]
# 算法调用
print(getResult(n, cans, musts))
免责声明:
评论0