题目描述
游戏里面,队伍通过匹配实力相近的对手进行对战。但是如果匹配的队伍实力相差太大,对于双方游戏体验都不会太好。
给定n个队伍的实力值,对其进行两两实力匹配,两支队伍实例差距在允许的最大差距d内,则可以匹配。
要求在匹配队伍最多的情况下匹配出的各组实力差距的总和最小。
输入描述
第一行,n,d。队伍个数n。允许的最大实力差距d。
- 2<=n <=50
- 0<=d<=100
第二行,n个队伍的实力值空格分割。
- 0<=各队伍实力值<=100
输出描述
匹配后,各组对战的实力差值的总和。若没有队伍可以匹配,则输出-1。
用例
| 输入 | 6 30 81 87 47 59 81 18 |
| 输出 | 57 |
| 说明 | 18与47配对,实力差距29 59与81配对,实力差距22 81与87配对,实力差距6 总实力差距29+22+6=57 |
| 输入 | 6 20 81 87 47 59 81 18 |
| 输出 | 12 |
| 说明 |
最多能匹配成功4支队伍。 81与81配对,实力差距0。 总实力差距12+0=12 |
| 输入 | 4 10 40 51 62 73 |
| 输出 | -1 |
| 说明 | 实力差距都在10以上, 没有队伍可以匹配成功。 |
题目解析
本题要求在匹配队伍最多的情况下匹配出的各组实力差距的总和最小
即两个要求:
- 匹配队伍最多
- 各匹配实力差之和最小
且最终结果要优先满足“匹配队伍最多”,其次满足“各匹配实力差之和最小”
而两个队伍是否能够匹配,也有要求
两支队伍实例差距在允许的最大差距d内,则可以匹配
因此队伍匹配也要考虑实力差。
解决本题时,我们可以先不考虑两个队伍实力差对队伍匹配的影响,即可以把 d 值当成无穷大的。
那么此时,“匹配队伍最多”这个要求,已经形同虚设,为什么呢?
因为任意两个队伍都能匹配,那么只要队伍个数给定了,那么匹配数也就确定了,比如10个队伍,可以匹配5组,这5组就是最多的匹配情况。再比如7个队伍,最多可以匹配3组。
因此,此时我们只需要考虑最小实力差之和的问题了。
那么如何才能让 各匹配的实力差之和 最小呢?
此时我们应该让队伍实力值进行升序,这样每个队伍和其相邻的队伍形成的匹配的实力差是最小的。
比如下面用例的实力值就是升序的
7 100000
1 2 10 13 21 26 27
比如
- 1,2进行匹配,要比1,10进行匹配更优
- 10,13进行匹配,要比10,1进行匹配更优
此时,最优匹配策略,其实就是相邻队伍进行匹配。
对于偶数n个队伍而言,可以产生 n/2 个匹配,且为了最终各匹配实力差之和最小,应该顺序的两两相邻进行匹配,如果队伍用序号表示的话,则可以表示为:
[0, 1],[2, 3],[4, 5],[6, 7],….,[n-2, n-1]
对于奇数m个队伍而言,可以产生(m – 1) / 2 个匹配,即必须舍弃一个队伍,此时匹配该如何选呢?
如果队伍实力值升序后为:
a,b,c,d,e,f,g
那么可能大家最直观的匹配策略就是
[a, b],[c, d],[e, f] // 即舍弃g
或者
[g, f],[e, d],[c, b] // 即舍弃a
上面两种匹配策略其实就是:
- 正方向的,顺序的(保证实力差最小),两两匹配
- 负方向的,顺序的(保证实力差最小),两两匹配
这两种匹配策略产生的匹配个数是相同的,但是实力差之和谁更小,却无法确定。我们只能从中选取最小的。
但是上面策略是存在漏洞的,比如正向匹配策略中:
[a, b],[c, d],[e, f] // 即舍弃g
我们舍弃了g,那么是否可以保证:
[e, f]匹配的实力差,就一定比[f, g]匹配的实力差更小呢?
答案是:无法保证
因此,此时对于正向匹配有两种策略:
[a, b],[c, d],[e, f]
[a, b],[c, d],[f, g]
我们应该取其中最小的。
对于负向匹配策略,也是同理:
[g, f],[e, d],[c, b]
[g, f],[e, d],[b, a]
我们应该取其中最小的。
好的,到此本题最难的逻辑已经说明清楚了,接下来就是解开之前埋下的雷了:
我们可以先不考虑两个队伍实力差对队伍匹配的影响,即可以把 d 值当成无穷大的。
实际用例中,不可能都是 d 值无穷大的。必然存在 d 值,让一些队伍之间无法进行匹配。
其实,解决这个问题很简单,我们其实已经对队伍实力值进行升序了,那么接下来可以对他再进行“分段处理”。
怎么分段呢?比如用例2
6 20
81 87 47 59 81 18
实力值升序后为:
18 47 59 81 81 87
其中
- 18和相邻队伍47的实力差是29,而d值是20,因此18和47无法组队,同时18肯定无法和后面其他队伍进行匹配了,因为后面队伍的实力值要比47更大。因此18就是一段。
- 47和相邻队伍59的实力差是12,因此可以组队,而59和相邻队伍81的实力差是22,而d值是20,因此59和81无法组队。因此47,59就是一段。
- 同理81,81,87也是一段。
因此,上面队伍其实分为了三段:
18- 47,59
- 81,81,87
由于队伍匹配至少两个,因此分段18被排除。我们只需要讨论剩余的两个分段。此时对于每个分段来说,我们就可以采用正向匹配策略和负向匹配策略来获得结果。
下面代码中,我并没有按照队伍实力值得粒度进行分段,而是直接在分段过程中,计算出匹配队伍得实力差,即:分段记录得是两两匹配的实力差,上面按照队伍的分段,可以修改为实力差分段
- 12 // 即59-47
- 0,6 // 即81-81,87-81
此时,我们正向匹配或者负向匹配时,只能跳着选,比如分段0,6,我们选了0,就不能选6,因为0,6其实共用了一个队伍81。
我们还是用一个用例来演示下正向匹配:
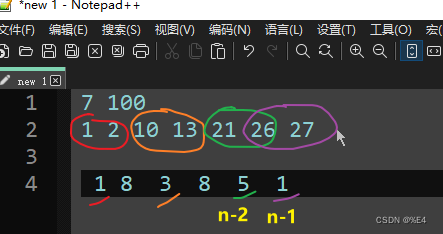
- 第2行是实力值
- 第4行是顺序的两两队伍实力差
可以发现,对于奇数个队伍而言,正向匹配的话,其实就是从第0个实力差开始选,然后隔一个选一个,即按照序号选的话,就是0,2,4,6,….,n-2
但是最后三个队伍,比如上图21,26,27,我们应该选择【21,26】和【26,27】中较小的,其实就是对于最后两个实力差5,1中选择较小的。
抽象了来说,其实就是实力差数组序号n-2,n-1中选最小的。
同理,对于负向匹配而言,其实就是实力差数组序号0,1中选最小的。
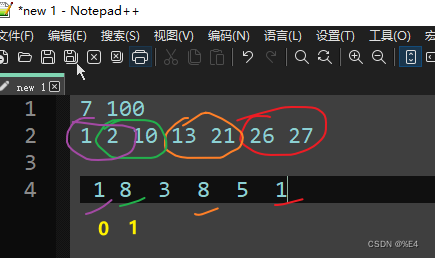
2023.05.06 上面算法存在一个问题,我们可以通过一个反例来说明:
7 100
1 2 6 15 17 17 20
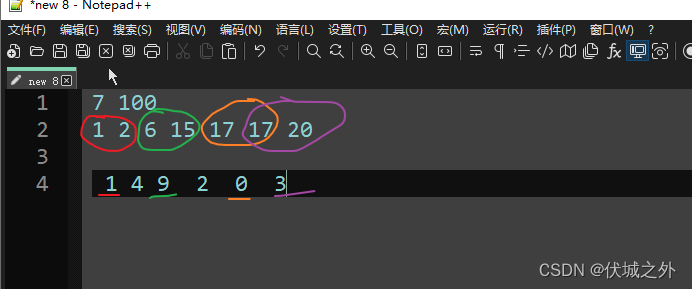
按照前面的思路,我们应该选择1+9+0的匹配策略,但是其实这并非最优策略,最优策略应该如下
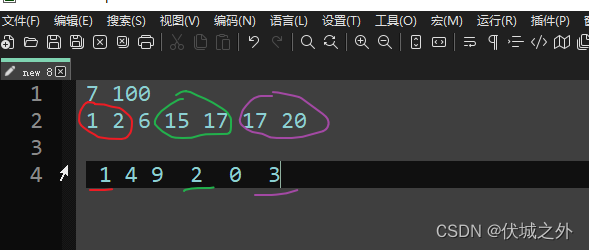
即 1 + 2 + 3 匹配策略。
假设现在有实力差数组diffs,一个实力差值就是两个相邻队伍的匹配,因此我们不能选择相邻的实力差,因为这样会造成一个队伍被左右相邻的队伍同时匹配,因此实力差数组要按照不相邻选取原则:
- 对于奇数个的实力差数组,最多匹配数必然是 ( diffs.length + 1 ) / 2,只有一个选取策略,如下图是一个实力差列表,其中黄色的就是被选择的匹配,此时满足最多匹配
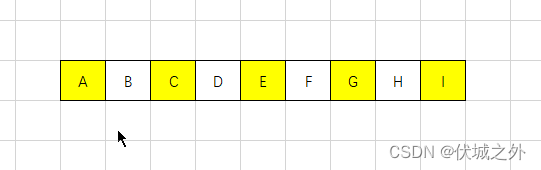
- 对于偶数个的实力差数组,最多匹配数必然是 diffs.length / 2,此时有如下选取策略
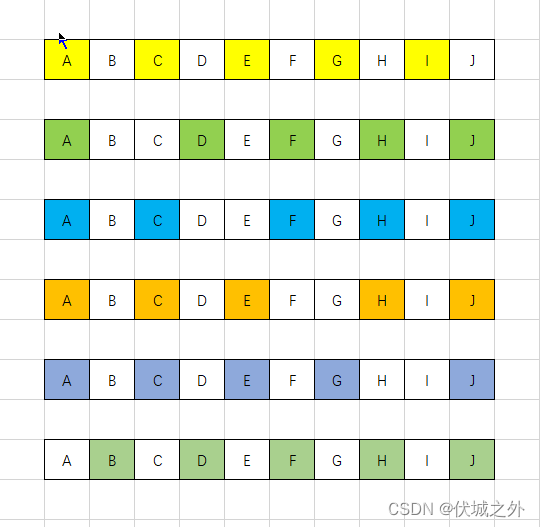
可以发现,在选取过程中,我们最多只能有一次,间隔两位后选取的,其他情况都是间隔一位后选取。
因为,如果发生两次或以上的间隔两位后选取,那么就无法保证最多匹配数了。
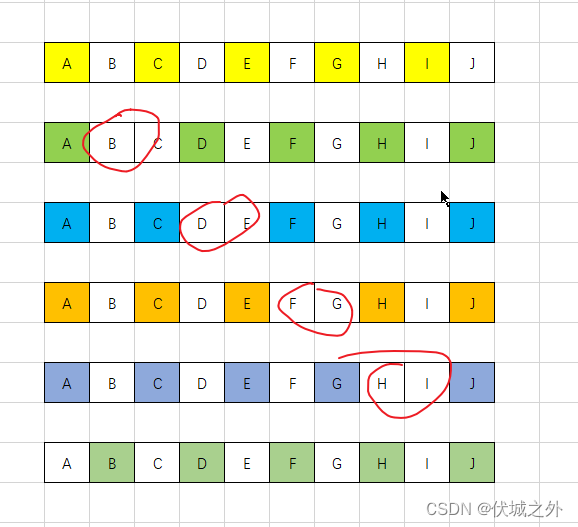
因此,本题的难度就大大降低了。
我们可以定义一个abandon标志,初始为false,表示还没有进行间隔两位的选取动作。
当abandon为false时,此时我们有两种选取策略:
- “选” 当前实力差diffs[index],实力差之和+=diffs[index],下次从diffs[index + 2]开始选取
- “不选” 当前实力差diffs[index],实力差之和不变,下次从diffs[index + 2]开始选取,但是abandon被修改为true
当abandon为true时,此时我们只有一种选取策略,那就是必然”选取“当前实力差diffs[index]
Java算法源码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int d = sc.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
System.out.println(getResult(n, d, arr));
}
/**
* @param n 队伍个数n
* @param d 允许的最大实力差距d
* @param arr n个队伍的实力值数组
* @return 匹配队伍最多的情况下匹配出的各组实力差距的总和最小
*/
public static int getResult(int n, int d, int[] arr) {
// 实力数组升序
Arrays.sort(arr);
// ans记录各组实力差之和
// int ans = 0;
int res = 0;
// 此flag标记是否没有队伍可以匹配,true表示没有队伍可以匹配,此时应该返回-1
boolean flag = true;
// segment用于保存分段
ArrayList<Integer> segment = new ArrayList<>();
for (int i = 1; i < n; i++) {
// 相邻两队的实力差diff
int diff = arr[i] - arr[i - 1];
// 如果diff大于d,那么说明 i - 1 无法和 i 组队匹配
if (diff > d) {
// 此时分段开始
if (segment.size() > 0) {
flag = false;
int[] ans = {Integer.MAX_VALUE};
getMaxCountMinSum(segment, 0, false, 0, ans); // 计算分段部分的组队匹配的:匹配队伍最多的情况下匹配出的各组实力差距的最小总和
res += ans[0];
segment.clear(); // 开始记录新的分段
}
} else {
segment.add(diff); // 如果diff不大于d,那么说明 i - 1 可以和 i 组队匹配,此时将实力差(相当于一个组队匹配)计入分段
}
}
// 最后一个分段也要记得处理,上面逻辑无法将最后一个分段处理到
if (segment.size() > 0) {
flag = false;
int[] ans = {Integer.MAX_VALUE};
getMaxCountMinSum(segment, 0, false, 0, ans);
res += ans[0];
}
if (flag) {
return -1;
}
return res;
}
public static void getMaxCountMinSum(
ArrayList<Integer> segment, int index, boolean abandon, int sum, int[] ans) {
if (index >= segment.size()) {
if (sum < ans[0]) ans[0] = sum;
return;
}
getMaxCountMinSum(segment, index + 2, abandon, sum + segment.get(index), ans);
if (!abandon && segment.size() % 2 == 0) {
getMaxCountMinSum(segment, index + 1, true, sum, ans);
}
}
}
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
const [n, d] = lines[0].split(" ").map(Number);
const arr = lines[1].split(" ").map(Number);
console.log(getResult(n, d, arr));
lines.length = 0;
}
});
/**
* @param {*} n 队伍个数n
* @param {*} d 允许的最大实力差距d
* @param {*} arr n个队伍的实力值数组
* @return 匹配队伍最多的情况下匹配出的各组实力差距的总和最小
*/
function getResult(n, d, arr) {
// 实力数组升序
arr.sort((a, b) => a - b);
// ans记录各组实力差之和
let ans = 0;
// 此flag标记是否没有队伍可以匹配,true表示没有队伍可以匹配,此时应该返回-1
let flag = true;
// segment用于保存分段
let segment = [];
for (let i = 1; i < n; i++) {
// 相邻两队的实力差diff
const diff = arr[i] - arr[i - 1];
// 如果diff大于d,那么说明 i - 1 无法和 i 组队匹配
if (diff > d) {
// 此时分段开始
if (segment.length > 0) {
flag = false;
const minSum = [Infinity];
getMaxCountMinSum(segment, 0, false, 0, minSum); // 计算分段部分的组队匹配的:匹配队伍最多的情况下匹配出的各组实力差距的最小总和
ans += minSum[0];
segment.length = 0; // 开始记录新的分段
}
} else {
segment.push(diff); // 如果diff不大于d,那么说明 i - 1 可以和 i 组队匹配,此时将实力差(相当于一个组队匹配)计入分段
}
}
// 最后一个分段也要记得处理,上面逻辑无法将最后一个分段处理到
if (segment.length > 0) {
flag = false;
const minSum = [Infinity];
getMaxCountMinSum(segment, 0, false, 0, minSum);
ans += minSum[0];
}
if (flag) return -1;
return ans;
}
function getMaxCountMinSum(segment, index, abandon, sum, minSum) {
if (index >= segment.length) {
if (sum < minSum[0]) minSum[0] = sum;
return;
}
getMaxCountMinSum(segment, index + 2, abandon, sum + segment[index], minSum);
if (!abandon && segment.length % 2 == 0) {
getMaxCountMinSum(segment, index + 1, true, sum, minSum);
}
}
Python算法源码
# 输入获取
import sys
n, d = map(int, input().split())
arr = list(map(int, input().split()))
def getMaxCountMinSum(segment, index, abandon, total, minTotal):
if index >= len(segment):
if total < minTotal[0]:
minTotal[0] = total
return
getMaxCountMinSum(segment, index + 2, abandon, total + segment[index], minTotal)
if not abandon and len(segment) % 2 == 0:
getMaxCountMinSum(segment, index + 1, True, total, minTotal)
# 算法入口
def getResult(n, d, arr):
"""
:param n: 队伍个数n
:param d: 允许的最大实力差距d
:param arr: n个队伍的实力值数组
:return: 匹配队伍最多的情况下匹配出的各组实力差距的总和最小
"""
# 实力数组升序
arr.sort()
# ans记录各组实力差之和
ans = 0
# 此flag标记是否没有队伍可以匹配,true表示没有队伍可以匹配,此时应该返回-1
flag = True
# segment用于保存分段
segment = []
for i in range(1, n):
# 相邻两队的实力差diff
diff = arr[i] - arr[i - 1]
# 如果diff大于d,那么说明 i - 1 无法和 i 组队匹配
if diff > d:
# 此时分段开始
if len(segment) > 0:
flag = False
minTotal = [sys.maxsize]
getMaxCountMinSum(segment, 0, False, 0, minTotal) # 计算分段部分的组队匹配的:匹配队伍最多的情况下匹配出的各组实力差距的最小总和
ans += minTotal[0]
segment.clear() # 开始记录新的分段
else:
# 如果diff不大于d,那么说明 i - 1 可以和 i 组队匹配,此时将实力差(相当于一个组队匹配)计入分段
segment.append(diff)
# 最后一个分段也要记得处理,上面逻辑无法将最后一个分段处理到
if len(segment) > 0:
flag = False
minTotal = [sys.maxsize]
getMaxCountMinSum(segment, 0, False, 0, minTotal)
ans += minTotal[0]
if flag:
return -1
return ans
# 算法调用
print(getResult(n, d, arr))
免责声明:
评论0