题目描述
一个快递公司希望在一条街道建立新的服务中心。公司统计了该街道中所有区域在地图上的位置,并希望能够以此为依据为新的服务中心选址:使服务中心到所有区域的距离的总和最小。
给你一个数组positions,其中positions[i] = [left, right] 表示第 i 个区域在街道上的位置,其中left代表区域的左侧的起点,right代表区域的右侧终点,假设服务中心的位置为location:
- 如果第 i 个区域的右侧终点right满足 right < location,则第 i 个区域到服务中心的距离为 location – right;
- 如果第 i 个区域的左侧起点left 满足 left > location,则第 i 个区域到服务中心的距离为left – location;
- 如果第 i 个区域的两侧left,right满足left <= location <= right,则第 i 个区域到服务中心的距离为0
选择最佳的服务中心位置为location,请返回最佳的服务中心位置到所有区域的距离总和的最小值。
输入描述
先输入区域数组positions的长度n(1 ≤ n ≤ 10^5)
接下来 n 行每行输入成对的left和right值,以空格隔开
- -10^9 <left ≤ 10^9
- -10^9 <right ≤ 10^9
输出描述
输出为location
用例
| 输入 | 3 1 2 3 4 10 20 |
| 输出 | 8 |
| 说明 | 无 |
| 输入 | 2 1 4 4 5 |
| 输出 | 0 |
| 说明 | 无 |
| 输入 | 4 5 6 1 8 7 15 2 4 |
| 输出 | 3 |
| 说明 | 无 |
| 输入 | 6 1 3 4 9 2 15 6 27 15 17 5 8 |
| 输出 | 12 |
| 说明 | 无 |
| 输入 | 16 41 67 0 34 24 69 58 78 62 64 5 45 27 81 61 91 42 95 27 36 4 91 2 53 82 92 16 21 18 95 26 47 |
| 输出 | 127 |
| 说明 | 无 |
题目解析
根据网友反馈进行分析得出,本题中各区域应该是有交集的。
我想了很久,如何求解某个点到有交集区域的最小距离和,但是没有什么好的办法,直到我死心准备用暴力法求解时,发现了一丝丝生机。下面是暴力法测试过程:
测试用例:含区域交集情况
11
-10 10
1 2
3 4
5 10
6 8
7 12
9 13
15 20
31 41
22 35
34 50
JavaScript暴力实现
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
n = lines[0] - 0;
}
if (n && lines.length === n + 1) {
const positions = lines.slice(1).map((line) => line.split(" ").map(Number));
console.log(getResult(n, positions));
lines.length = 0;
}
});
function getResult(n, positions) {
const tmp = positions.flat(2).sort((a, b) => a - b);
let min = tmp.at(0);
let max = tmp.at(-1);
let ans = Infinity;
for (let i = min; i <= max; i += 0.5) {
let dis = 0;
for (let position of positions) {
const [l, r] = position;
if (r < i) dis += i - r;
else if (i < l) dis += l - i;
}
console.log(i, dis); // 服务中心选址 i 位置,dis为该位置服务中心到所有区间的距离之和
ans = Math.min(ans, dis);
}
return ans;
}
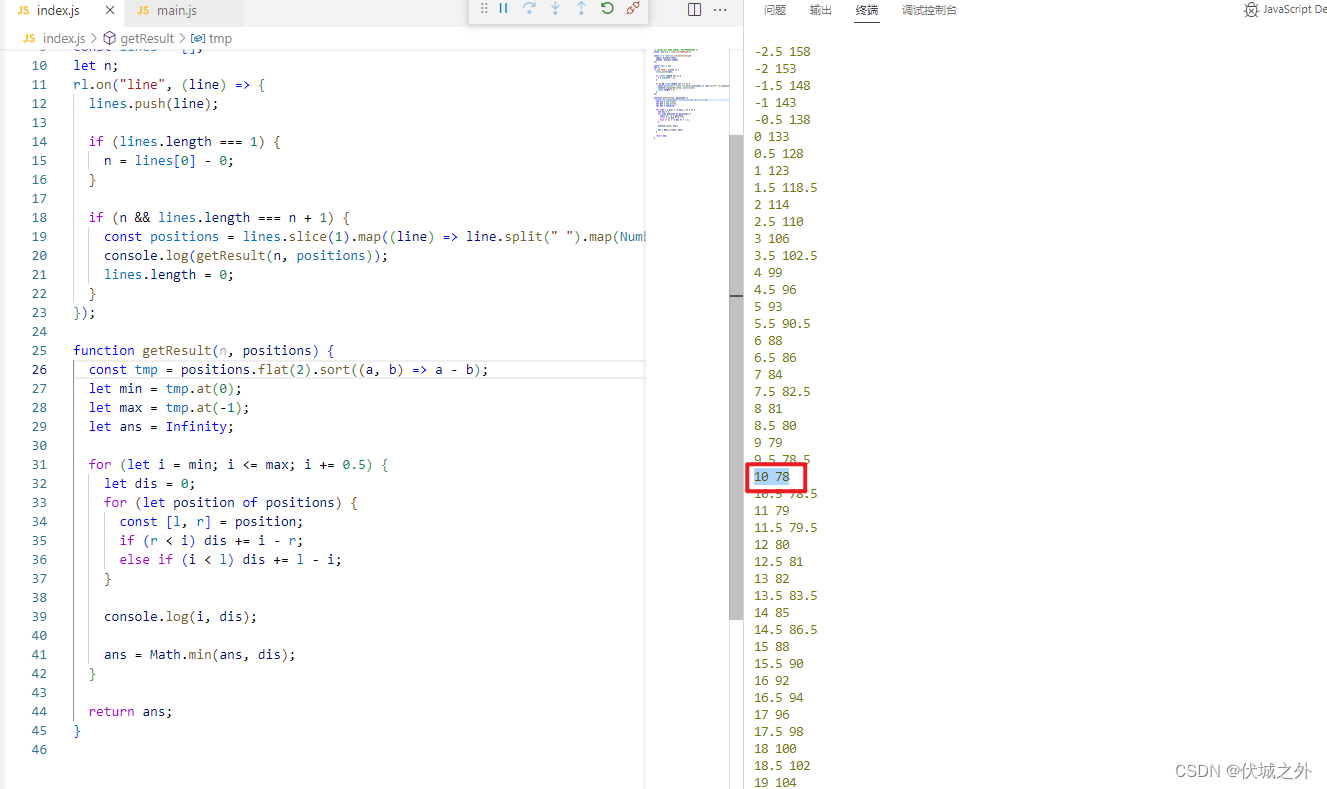
可以发现,当服务中心选址10位置时,到各区间距离之和最小为78
Java暴力实现
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
double[][] positions = new double[n][2];
for (int i = 0; i < n; i++) {
positions[i][0] = sc.nextInt();
positions[i][1] = sc.nextInt();
}
System.out.println(getResult(n, positions));
}
public static double getResult(int n, double[][] positions) {
ArrayList<Double> tmp = new ArrayList<>();
for (double[] pos : positions) {
tmp.add(pos[0]);
tmp.add(pos[1]);
}
tmp.sort(Double::compareTo);
double min = tmp.get(0);
double max = tmp.get(tmp.size() - 1);
double ans = Double.MAX_VALUE;
for (double i = min; i <= max; i += 0.5) {
double dis = 0;
for (double[] pos : positions) {
double l = pos[0];
double r = pos[1];
if (r < i) dis += i - r;
else if (i < l) dis += l - i;
}
System.out.println(i + "t" + dis);
ans = Math.min(ans, dis);
}
return ans;
}
}
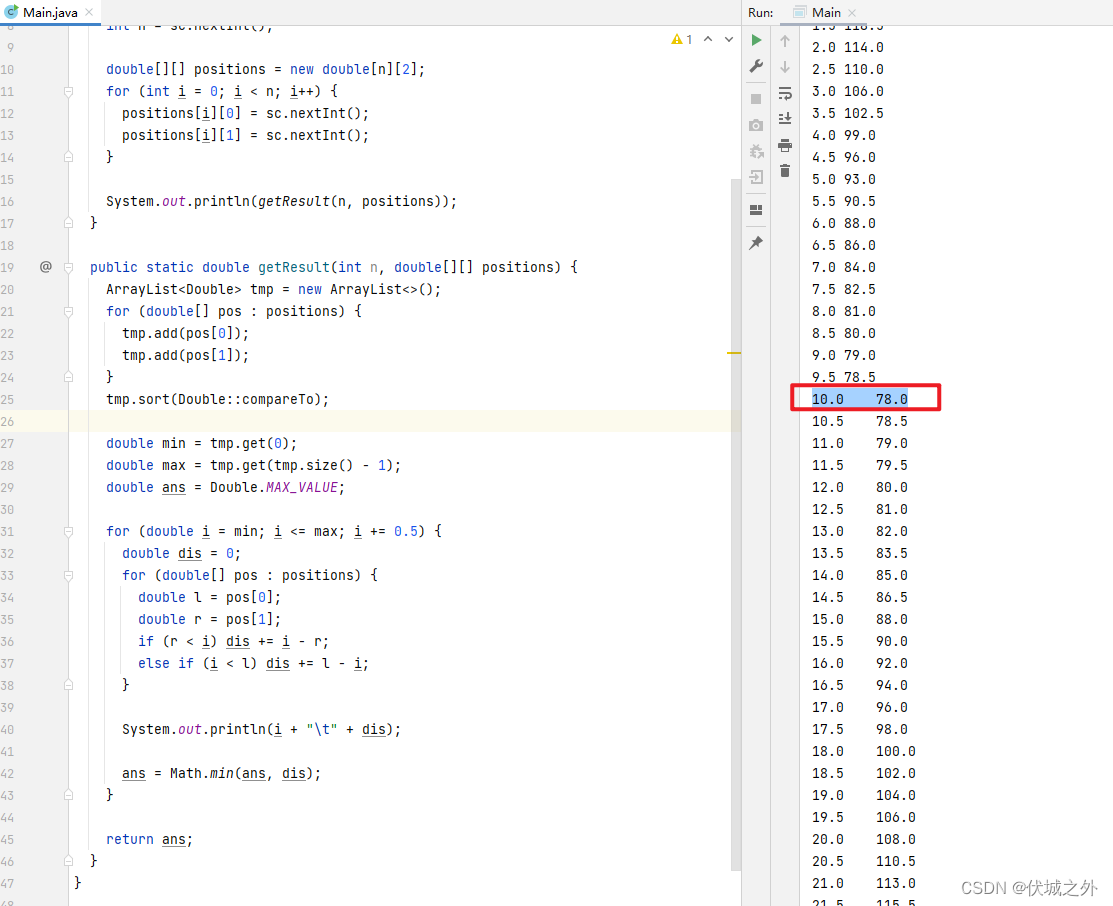
可以发现,当服务中心选址10位置时,到各区间距离之和最小为78
Python暴力实现
import math
import sys
# 输入获取
n = int(input())
positions = [list(map(int, input().split())) for i in range(n)]
# 算法入口
def getResult(n, positions):
tmp = []
for pos in positions:
tmp.append(pos[0])
tmp.append(pos[1])
tmp.sort()
minP = tmp[0]
maxP = tmp[-1]
ans = sys.maxsize
i = minP
while i <= maxP:
dis = 0
for l, r in positions:
if r < i:
dis += i - r
elif i < l:
dis += l - i
print(str(i) + "t" + str(dis))
ans = min(ans, dis)
i += 0.5
return ans
# 算法调用
print(getResult(n, positions))
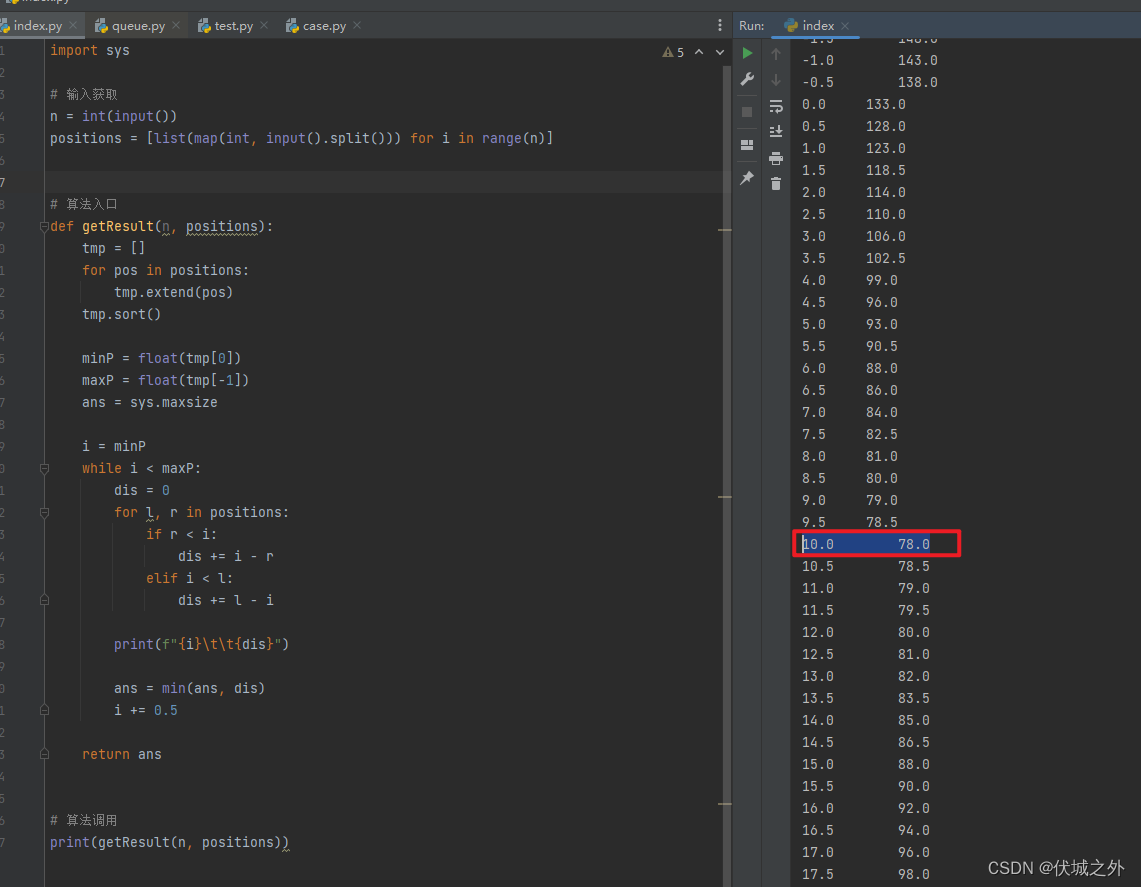
可以发现,当服务中心选址10位置时,到各区间距离之和最小为78
上面暴力法过程中,我首先获得了所有区间中最左边的点min,和最右边的点max,并遍历这两个点之间每一个点作为服务中心地址 i ,并求每个服务中心地址到各区域的距离之和 dis,然后将它们成对打印出来,结果发现一个现象:
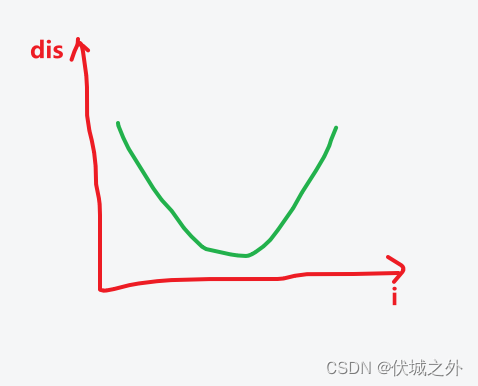
随着 服务中心位置 i 的变化,服务中心到各区域的距离之和 dis 呈现上图U型曲线。
即,一定存在一个 i ,其左边点 i-0.5 的,和其右边点 i+0.5 到各区域的距离和大于它。
因此,我想是否可以用二分法求解,即取min点和max点的中间点mid作为服务中心位置,:
- 如果 dis(mid – 0.5) >= dis(mid) && dis(mid+0.5) >= dis(mid),则 mid 就是所求的点
- 如果 dis(mid – 0.5 ) > dis(mid) > dis(mid +0.5),则说明当前 mid 点处于上图的下降区间,此时我们应该将mid作为新的min值,然后重新取min,max的中间点作为新mid
- 如果 dis(mid – 0.5 ) < dis(mid) < dis(mid +0.5),则说明当前 mid 点处于上图的上升区间,此时我们应该将mid作为新的max值,然后重新取min,max的中间点作为新mid
这样一搞,我们最终就可以找到最低dis的mid点。
2023.04.12 上面的二分策略存在问题,本题要求解凹函数的极值,应该使用三分法求解。
关于三分法请看:
2023.04.19 今天又有考友考到这题了,上面解法还是27%通过率。我已经emo了。
然后我又读了一遍题目,发现:
- 题目描述:请返回最佳的服务中心位置到所有区域的距离总和的最小值
- 输出描述:输出为location
- 用例:输出的是最佳的服务中心位置到所有区域的距离总和的最小值
难道实际机试系统要求输出的是:服务中心的位置?
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, positions;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
n = lines[0] - 0;
}
if (n && lines.length === n + 1) {
positions = lines.slice(1).map((line) => line.split(" ").map(Number));
console.log(getResult(n, positions));
lines.length = 0;
}
});
function getResult() {
const tmp = positions.flat(2).sort((a, b) => a - b);
let l = tmp.at(0);
let r = tmp.at(-1);
const eps = 1e-5;
while (r - l >= eps) {
const k = (r - l) / 3;
const ml = l + k;
const mr = r - k;
if (getDistance(ml) < getDistance(mr)) {
r = mr;
} else {
l = ml;
}
}
return Math.floor(getDistance(l));
}
function getDistance(t) {
let dis = 0;
for (let [l, r] of positions) {
if (r < t) dis += t - r;
else if (t < l) dis += l - t;
}
return dis;
}
Java算法源码
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
static double[][] positions;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
positions = new double[n][2];
for (int i = 0; i < n; i++) {
positions[i][0] = sc.nextDouble();
positions[i][1] = sc.nextDouble();
}
System.out.println(getResult());
}
public static int getResult() {
ArrayList<Double> tmp = new ArrayList<>();
for (double[] pos : positions) {
tmp.add(pos[0]);
tmp.add(pos[1]);
}
tmp.sort(Double::compareTo);
double l = tmp.get(0);
double r = tmp.get(tmp.size() - 1);
double eps = 1e-5;
while (r - l >= eps) {
double k = (r - l) / 3;
double ml = l + k;
double mr = r - k;
if (getDistance(ml) < getDistance(mr)) {
r = mr;
} else {
l = ml;
}
}
return (int) getDistance(l);
}
public static double getDistance(double t) {
double dis = 0;
for (double[] pos : positions) {
double l = pos[0];
double r = pos[1];
if (r < t) dis += t - r;
else if (t < l) dis += l - t;
}
return dis;
}
}
Python算法源码
import math
# 输入获取
n = int(input())
positions = [list(map(float, input().split())) for _ in range(n)]
# 算法入口
def getResult():
tmp = []
for pos in positions:
tmp.extend(pos)
tmp.sort()
l = tmp[0]
r = tmp[-1]
eps = 1e-5
while r - l >= eps:
k = (r - l) / 3
ml = l + k
mr = r - k
if getDistance(ml) < getDistance(mr):
r = mr
else:
l = ml
return int(getDistance(l))
def getDistance(t):
dis = 0
for l, r in positions:
if r < t:
dis += t - r
elif t < l:
dis += l - t
return dis
# 算法调用
print(getResult())
免责声明:
评论0