题目描述
已知树形结构的所有节点信息,现要求根据输入坐标(x,y)找到该节点保存的内容值,其中x表示节点所在的层数,根节点位于第0层,根节点的子节点位于第1层,依次类推;y表示节点在该层内的相对偏移,从左至右,第一个节点偏移0,第二个节点偏移1,依次类推;
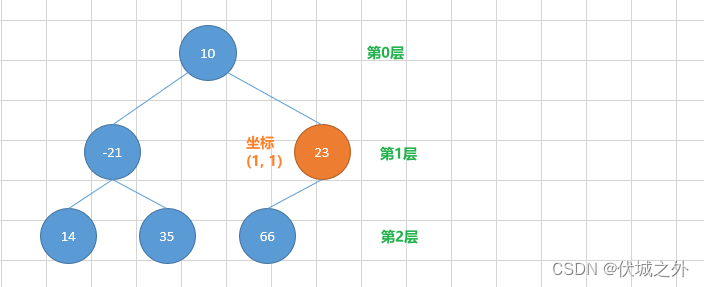
举例:上图中,假定圆圈内的数字表示节点保存的内容值,则根据坐标(1,1)查到的内容值是23。
输入描述
每个节点以一维数组(int[])表示,所有节点信息构成二维数组(int[][]),二维数组的0位置存放根节点;
表示单节点的一维数组中,0位置保存内容值,后续位置保存子节点在二维数组中的索引位置。
对于上图中:
- 根节点的可以表示为{10,1,2},
- 树的整体表示为{{10,1,2},{-21,3,4},{23,5},{14},{35},{66}}
查询条件以长度为2的一维数组表示,上图查询坐标为(1,1)时表示为{1,1}
使用Java标准IO键盘输入进行录入时,
- 先录入节点数量
- 然后逐行录入节点
- 最后录入查询的位置
对于上述示例为:
6
10 1 2
-21 3 4
23 5
14
35
66
1 1
输出描述
查询到内容时,输出{内容值},查询不到时输出{}
上图中根据坐标(1,1)查询输出{23},根据坐标(1,2)查询输出{}
用例
| 输入 | 6 10 1 2 -21 3 4 23 5 14 35 66 1 1 |
| 输出 | {23} |
| 说明 | 无 |
2023.1.16新增用例说明,之前代码只是根据用例1写的,误以为题目中说的树是二叉树,因此代码存在问题,后面发现了原题更多的用例说明,意识到本题的树是多叉树,但是本题代码中多叉树的处理逻辑和二叉树相同,只需要微调代码即可
| 输入 | 14 0 1 2 3 4 -11 5 6 7 8 113 9 10 11 24 12 35 66 13 77 88 99 101 102 103 25 104 2 5 |
| 输出 | {102} |
| 说明 | 无 |
| 输入 | 14 0 1 2 3 4 -11 5 6 7 8 113 9 10 11 24 12 35 66 13 77 88 99 101 102 103 25 104 3 2 |
| 输出 | {} |
| 说明 | 无 |
| 输入 | 1 1000 0 0 |
| 输出 | {1000} |
| 说明 | 无 |
题目解析
这题输入描述比较晦涩难懂,但我还是猜出来一点:
每个节点以一维数组(int[])表示,所有节点信息构成二维数组(int[][]),二维数组的0位置存放根节点;
这句话的意思就是:用例的第二行输入到倒数第二行输入可以构成一个二维数组,二维数组的元素是一维数组,如下图
[
[10,1,2],
[-21,3,4],
[23,5],
[14],
[35],
[66]
]
假设二维数组是matrix的话,则每一个matrix[i]对应树的一个节点,其中matrix[0] (如用例[10,1,2])代表的是树的根节点。
表示单节点的一维数组中,0位置保存内容值,后续位置保存子节点在二维数组中的索引位置。
上面这句话的意思是,matrix[i] (是一个一维数组),我们用arr = matrix[i],则arr[0]表示节点的内容值,arr[1]、arr[2]表示的是该节点的子节点在matrix中的索引位置。
比如[10,1,2]表示内容值为10的节点,有两个子节点,分别是matrix[1]和matrix[2],即[-21,3,4],[23,5]。
由于本题是二叉树,因此一个节点最多有两个子节点,最少没有子节点。
以上是关于输入描述的解读。
本题并没有说二叉树是完全二叉树,因此二叉树的节点非常有可能像:
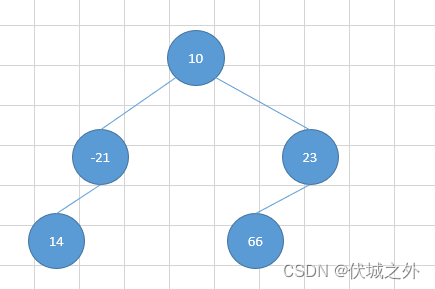
因此无法直接利用完全二叉树特性。
但是也不难,本题就是就是一个简单的深度优先搜索题
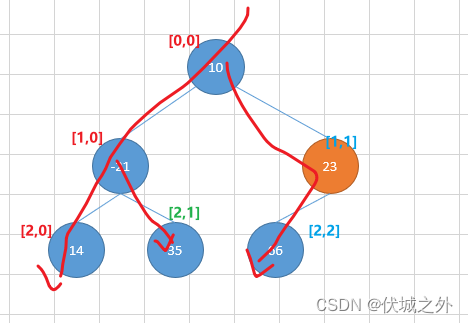
本题的意思其实就是让我们再构造一个二维数组matrix2,这个二维数组形式如上图所示,具体内容如下
[
[10],
[-21, 23],
[14,35,66]
]
因此,我们很容想到利用深度优先搜索,从根节点开始递归,dfs(root, 0),dfs参数含义是:当前节点root,得到的节点值将放置于二维数组matrix2的第0行。
从根节点还可以得到其左右子节点的索引,因此我们可以继续递归其左右子节点 dfs(left, 1)、dfs(right,1),只是此时的得到的子节点将放于matrix2的第1行。
由此,我们就可以将节点值放到正确的行位置上了。
那么列位置该如何确认呢?
很好解决,matrix2的每一行都是一个数组,由于我们是优先左子树遍历,因此,总是每一行最左边的节点被优先遍历出来,我们只需要将遍历出来的节点值push压入对应行的数组中即可。比如:
matrix2一开始是空数组[],然后遍历得到根节点,压入第0行的数组元素中,但是第0行没有数组元素,因此就构造一个[val]压入,同理处理根节点的左子节点,然后继续处理左子节点的左子节点,因此第一个深搜回溯时,得到
[
[10],
[-21],
[14]
]
即确认了每一行数组的第一个元素,刚好是
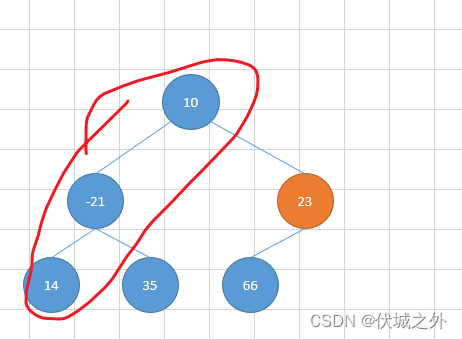
然后回溯过程将其余节点值依次加入每一行数组中,最终得到
[
[10],
[-21, 23],
[14,35,66]
]
此时,找任意位置的节点值都是so easy
2023.03.17 补充一个用例
本题中最后一行输入的目标节点坐标位置可能是负数,尼玛,我服了,比如下面用例
6
10 1 2
-21 3 4
23 5
14
35
66
-1 -1
如果坐标位置为负数,则会出现数组越界的问题,加了这个就100%了
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
n = lines[0] - 0;
}
if (n && lines.length === n + 2) {
lines.shift();
const [tx, ty] = lines.pop().split(" ").map(Number);
const nodes = lines.map((line) => line.split(" ").map(Number));
console.log(getResult(nodes, tx, ty));
lines.length = 0;
}
});
/**
*
* @param {*} nodes 数组,存储树中所有节点,数组元素node也是数组,node = [val, left, right] ,其中val是node节点的内容值,left是node节点的左子节点的索引,right是node节点的右子节点的索引,索引是相对nodes而言的
* @param {*} tx 目标位置x坐标
* @param {*} ty 目标位置y坐标
*/
function getResult(nodes, tx, ty) {
// 2023.03.17,尼玛,谁能想到还有tx,ty小于0的用例,题目描述一点没说
if (tx < 0 || ty < 0) return "{}";
const matrix = [];
function dfs(node, level) {
if (!node) return;
// 2023.1.16更新代码逻辑,之前本题只有用例1,因此误以为题目中的树指的是二叉树,因此错误意味一个节点最多只有两个子节点,但是后面补充了更多用例,发现本题的树是多叉树
// const [val, left, right] = node;
const val = node[0];
matrix[level] ? matrix[level].push(val) : (matrix[level] = [val]);
// 2023.1.16更新代码逻辑,之前本题只有用例1,因此误以为题目中的树指的是二叉树,因此错误意味一个节点最多只有两个子节点,但是后面补充了更多用例,发现本题的树是多叉树
// dfs(nodes[left], level + 1);
// dfs(nodes[right], level + 1);
for (let i = 1; i < node.length; i++) {
dfs(nodes[node[i]], level + 1);
}
}
dfs(nodes[0], 0);
if (matrix[tx] && matrix[tx][ty]) {
return `{${matrix[tx][ty]}}`;
} else {
return "{}";
}
}
Java算法源码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static ArrayList<Integer[]> nodes;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
nodes = new ArrayList<>();
for (int i = 0; i < n; i++) {
Integer[] node =
Arrays.stream(sc.nextLine().split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
nodes.add(node);
}
int tx = sc.nextInt();
int ty = sc.nextInt();
System.out.println(getResult(nodes, tx, ty));
}
public static String getResult(ArrayList<Integer[]> nodes, int tx, int ty) {
// 2023.03.17,尼玛,谁能想到还有tx,ty小于0的用例,题目描述一点没说
if (tx < 0 || ty < 0) return "{}";
ArrayList<ArrayList<Integer>> matrix = new ArrayList<>();
dfs(matrix, nodes.get(0), 0);
if (tx < matrix.size() && ty < matrix.get(tx).size()) {
return "{" + matrix.get(tx).get(ty) + "}";
} else {
return "{}";
}
}
public static void dfs(ArrayList<ArrayList<Integer>> matrix, Integer[] node, Integer level) {
if (node == null) return;
int val = node[0];
if (level < matrix.size()) {
matrix.get(level).add(val);
} else {
ArrayList<Integer> list = new ArrayList<>();
list.add(val);
matrix.add(list);
}
// 将二叉树处理逻辑,改成多叉树
// if (node.length > 1) {
// int left = node[1];
// dfs(matrix, nodes.get(left), level + 1);
// }
//
// if (node.length > 2) {
// int right = node[2];
// dfs(matrix, nodes.get(right), level + 1);
// }
for (int i = 1; i < node.length; i++) {
int child = node[i];
dfs(matrix, nodes.get(child), level + 1);
}
}
}
Python算法源码
# 输入获取
n = int(input())
nodes = [list(map(int, input().split())) for i in range(n)]
tx, ty = map(int, input().split())
# 算法入口
def getResult(nodes, tx, ty):
if tx < 0 or ty < 0:
return "{}"
matrix = []
dfs(matrix, nodes[0], 0)
if tx < len(matrix) and ty < len(matrix[tx]):
return "{" + str(matrix[tx][ty]) + "}"
else:
return "{}"
def dfs(matrix, node, level):
if node is None:
return
val = node[0]
if level < len(matrix):
matrix[level].append(val)
else:
matrix.append([val])
for i in range(1, len(node)):
child = node[i]
dfs(matrix, nodes[child], level + 1)
# 算法调用
print(getResult(nodes, tx, ty))
免责声明:
评论0