题目描述
定义字符串完全由 ‘A’ 和 ‘B’组成,当然也可以全是’A’或全是’B’。如果字符串从前往后都是以字典序排列的,那么我们称之为严格递增字符串。
给出一个字符串s,允许修改字符串中的任意字符,即可以将任何的’A’修改成’B’,也可以将任何的’B’修改成’A’,
求可以使s满足严格递增的最小修改次数。
0 < s的长度 < 100000。
输入描述
输入一个字符串: “AABBA”
输出描述
输出:1
用例
| 输入 | AABBA |
| 输出 | 1 |
| 说明 | 修改最后一位得到AABBB。 |
题目解析
新增一个用例:
AAABAAABBBBABB
该用例只需要修改两次。
我的解题思路如下:
首先,我们需要记录字符串长度为total,然后统计字符串中A的数量,记为A。
然后用动态规划,即定义一个dp数组,dp[i]的含义是 [0,i]闭区间内有多少个A。
统计好后,我们可以假设将 0 ~ i 闭区间内全部变成A,需要修改多少次?
0~i闭区间内理论会有 i+1 个A,而目前有dp[i] 个A,因此需要修改 i + 1 – dp[i] 次。
接着考虑将 i+1 ~ str.length-1 区间内全部变成B,需要修改多少次?
dp[i]表示 0~i闭区间内A的数量,那么 i+1~str.length-1 区间内A的数量= A – dp[i]
因此需要修改A – dp[i]次
因此,一共需要修改 i + 1 – dp[i] + A – dp[i] 次
我们从 0 ~ str.length-1 遍历出每一个 i 带入上面公式,保留最小的结果,就是题解。
另外,本题0 < s的长度 < 100000,如果使用dp数组的话,最坏需要定义一个100000长度的数组,这是有可能爆内存的,因此,下面代码中我不是dp数组,直接使用leftA变量。
补充一下:上面逻辑遗漏考虑两个分界线位置:
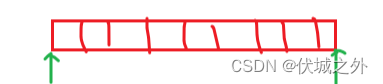
如上图所示,分别是-1索引位置和n索引位置,即上图两个绿色箭头位置。
前面逻辑,只考虑分界线位置在数组索引的0~n-1,因此当用例如下时:
BBABB
使用上面逻辑会产生问题。
此时,我们应该记录将字符串全部修改为A的次数,和全部修改为B的次数,即上面两个绿色箭头分界线。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
console.log(getResult(line));
});
function getResult(str) {
const total = str.length;
const A = str.replaceAll("B", "").length; // 字符串str中共有多少个A
// 如果全B或全A,则直接返回0
if (A == 0 || A == total) return 0;
// 修改为全A或者全B的次数取最小值
let ans = Math.min(A, total - A);
let leftA = 0;
for (let i = 0; i < total; i++) {
if (str[i] == "A") leftA++;
ans = Math.min(i + 1 - leftA + A - leftA, ans);
}
return ans;
}
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str = sc.next();
System.out.println(getResult(str));
}
public static int getResult(String str) {
int total = str.length();
int A = str.replaceAll("B", "").length(); // 字符串str中共有多少个A
// 如果全B或全A,则直接返回0
if (A == 0 || A == total) return 0;
// 修改为全A或者全B的次数取最小值
int ans = Math.min(A, total - A);
int leftA = 0;
for (int i = 0; i < total; i++) {
if (str.charAt(i) == 'A') leftA++;
ans = Math.min(i + 1 - leftA + A - leftA, ans);
}
return ans;
}
}
Python算法源码
# 输入获取
s = input()
# 算法入口
def getResult(s):
total = len(s)
A = len(s.replace("B", "")) # 字符串str中共有多少个A
# 如果全B或全A,则直接返回0
if A == 0 or A == total:
return 0
# 修改为全A或者全B的次数取最小值
ans = min(A, total - A)
leftA = 0
for i in range(total):
if s[i] == 'A':
leftA += 1
ans = min(i + 1 - leftA + A - leftA, ans)
return ans
# 算法调用
print(getResult(s))
免责声明:
评论0