题目描述
IGMP 协议中,有一个字段称作最大响应时间 (Max Response Time) ,HOST收到查询报文,解折出 MaxResponsetime 字段后,需要在 (0,MaxResponseTime] 时间 (s) 内选取随机时间回应一个响应报文,如果在随机时间内收到一个新的查询报文,则会根据两者时间的大小,选取小的一方刷新回应时间。
最大响应时间有如下计算方式:
当 Max Resp Code < 128, Max Resp Time = Max Resp Code;
当 Max Resp Code ≥ 128,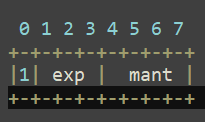
Max Resp Time = (mant | 0x10) << (exp + 3);
注: exp最大响应时间的高5~7位: mant 为最大响应时间的低4位。
其中接收到的MaxRespCode 最大值为 255,以上出现所有字段均为无符号数。
现在我们认为 HOST收到查询报文时,选取的随机时间必定为最大值,现给出 HOST 收到查询报文个数 C,HOST 收到该报文的时间T,以及查询报文的最大响应时间字段值 M,请计算出HOST 发送响应报文的时间。
输入描述
第一行为查询报文个数 C,后续每行分别为 HOST 收到报文时间 T,及最大响应时间M,以空格分割。
输出描述
HOST 发送响应报文的时间。
备注
用例确定只会发送一个响应报文, 不存在计时结束后依然收到查询报文的情况。
用例
| 输入 | 3 0 20 1 10 8 20 |
| 输出 | 11 |
| 说明 |
收到3个报文, 第8秒收到第3个报文,响应时间为20秒,则要到8+20=28秒响应,与第上面的报文的响应时间比较获得响应时间最小为11秒; 最终得到最小响应报文时间为11秒 |
| 输入 | 2 0 255 200 60 |
| 输出 | 260 |
| 说明 |
收到2个报文, 第200秒收到第2个报文,响应时间为60秒,则要到200+60-260秒响应,与第上面的报文的响应时间比较获得响应时间最小为260秒: 最终得到最小响应报文时间为260秒 |
题目解析
本题主要考察字符串操作。
每一个报文都一个最迟响应时间,即 t + getMaxResponseTime(m),我们只需要求出最小的最迟响应时间即可。
关于getMaxResponseTime的逻辑:
当 m < 128 时,m就是MaxResponseTime
当 m >= 128 时,需要将m转化为八位二进制字符串,取1~3范围作为exp,取4~7范围作为mant
然后再将exp和mant从二进制串转化为十进制,带入公式:(mant | 16) << (exp + 3) 求解即可。
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int c = sc.nextInt();
int[][] messages = new int[c][2];
for (int i = 0; i < c; i++) {
messages[i][0] = sc.nextInt();
messages[i][1] = sc.nextInt();
}
System.out.println(getResult(messages));
}
public static int getResult(int[][] messages) {
int ans = Integer.MAX_VALUE;
for (int[] message : messages) {
int respTime = message[0] + getMaxResponseTime(message[1]);
ans = Math.min(ans, respTime);
}
return ans;
}
public static int getMaxResponseTime(int m) {
if (m >= 128) {
StringBuilder bStr = new StringBuilder(Integer.toBinaryString(m));
int exp = Integer.parseInt(bStr.substring(1, 4), 2);
int mant = Integer.parseInt(bStr.substring(4), 2);
return (mant | 16) << (exp + 3);
} else {
return m;
}
}
}
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let c;
rl.on("line", (line) => {
lines.push(line);
if (lines.length == 1) {
c = parseInt(lines[0]);
}
if (c && lines.length == c + 1) {
lines.shift();
const messages = lines.map((s) => s.split(" ").map(Number));
console.log(getResult(messages));
lines.length = 0;
}
});
function getResult(messages) {
let ans = Infinity;
for (let [t, m] of messages) {
const respTime = t + getMaxResponseTime(m);
ans = Math.min(ans, respTime);
}
return ans;
}
function getMaxResponseTime(m) {
if (m >= 128) {
let bStr = Number(m).toString(2);
const exp = parseInt(bStr.slice(1, 4), 2);
const mant = parseInt(bStr.slice(4), 2);
return (mant | 16) << (exp + 3);
} else {
return m;
}
}
Python算法源码
import sys
# 输入获取
c = int(input())
messages = [list(map(int, input().split())) for _ in range(c)]
def getMaxResponseTime(m):
if m >= 128:
bStr = bin(m)[2:]
exp = int(bStr[1:4], 2)
mant = int(bStr[4:], 2)
return (mant | 16) << (exp + 3)
else:
return m
# 算法入口
def getResult():
ans = sys.maxsize
for t, m in messages:
respTime = t + getMaxResponseTime(m)
ans = min(ans, respTime)
return ans
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <limits.h>
#define MIN(a,b) ((a) < (b) ? (a) : (b))
int getMaxResponseTime(int m);
int res = INT_MAX;
int main() {
int c;
scanf("%d", &c);
int t, m;
for (int i = 0; i < c; i++) {
scanf("%d %d", &t, &m);
int respTime = t + getMaxResponseTime(m);
res = MIN(res, respTime);
}
printf("%dn", res);
return 0;
}
int getMaxResponseTime(int m) {
// Max Resp Code >= 128时,最大响应时间 = (mant | 0x10) << (exp + 3);
if(m >= 128) {
// 将十进制数 m 转成 二进制字符串对应的整型数组,比如 m = 255时,bin[8] = {1, 1, 1, 1, 1, 1, 1, 1};
int bin[8] = {0};
int i = 7;
while(m > 0) {
bin[i--] = m % 2;
m /= 2;
}
// j 0 1 2 3 4 5 6 7
// bin[] = {1, 1, 1, 1, 1, 1, 1, 1};
// exp截取bin的 j:1~3 范围,注意对应范围当成一个新的二进制数,因此j=3的位置是2^0
int exp = 0;
for(int j=1; j<4; j++) {
exp += bin[j] * (1 << (3 - j));
}
// mant截取bin的 j:4~7 范围,,注意对应范围当成一个新的二进制数,因此j=7的位置是2^0
int mant = 0;
for(int j=4; j<8; j++) {
mant += bin[j] * (1 << (7 - j));
}
// 0x10 等价于 16
return (mant | 16) << (exp + 3);
} else {
return m;
}
}免责声明:
评论0