题目描述
给航天器一侧加装长方形或正方形的太阳能板(图中的红色斜线区域),需要先安装两个支柱(图中的黑色竖条),再在支柱的中间部分固定太阳能板。
但航天器不同位置的支柱长度不同,太阳能板的安装面积受限于最短一侧的那根支柱长度。如图:
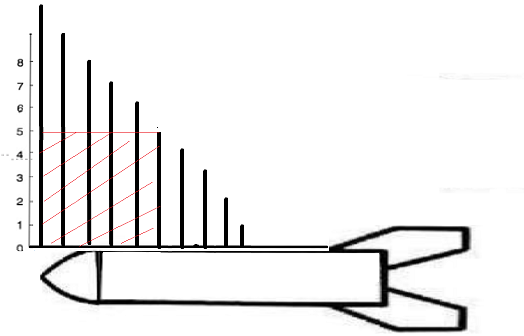
现提供一组整形数组的支柱高度数据,假设每根支柱间距离相等为1个单位长度,计算如何选择两根支柱可以使太阳能板的面积最大。
输入描述
10,9,8,7,6,5,4,3,2,1
注:支柱至少有2根,最多10000根,能支持的高度范围1~10^9的整数。柱子的高度是无序的,例子中递减只是巧合。
输出描述
可以支持的最大太阳能板面积:(10米高支柱和5米高支柱之间)
25
用例
| 输入 | 10,9,8,7,6,5,4,3,2,1 |
| 输出 | 25 |
| 备注 |
10米高支柱和5米高支柱之间宽度为5,高度取小的支柱高也是5,面积为25。 任取其他两根支柱所能获得的面积都小于25。 所以最大的太阳能板面积为25。 |
题目解析
首先想到的依旧是暴力破解
function getMaxArea(arr) {
let max = 0;
for (let i = 0; i < arr.length; i++) {
for (let j = i + 1; j < arr.length; j++) {
let x = j - i;
let y = Math.min(arr[i], arr[j]);
max = Math.max(max, x * y);
}
}
return max;
}
但是暴力破解是O(n^2)复杂度,随着数量规模的增大,算法效率会急剧下降,但是好在题目限制了支柱最多10000根,我测试了下10000的性能,差不多在160ms~200ms之间
双指针解法:
一开始i指针指向0,j指针指向arr.length-1
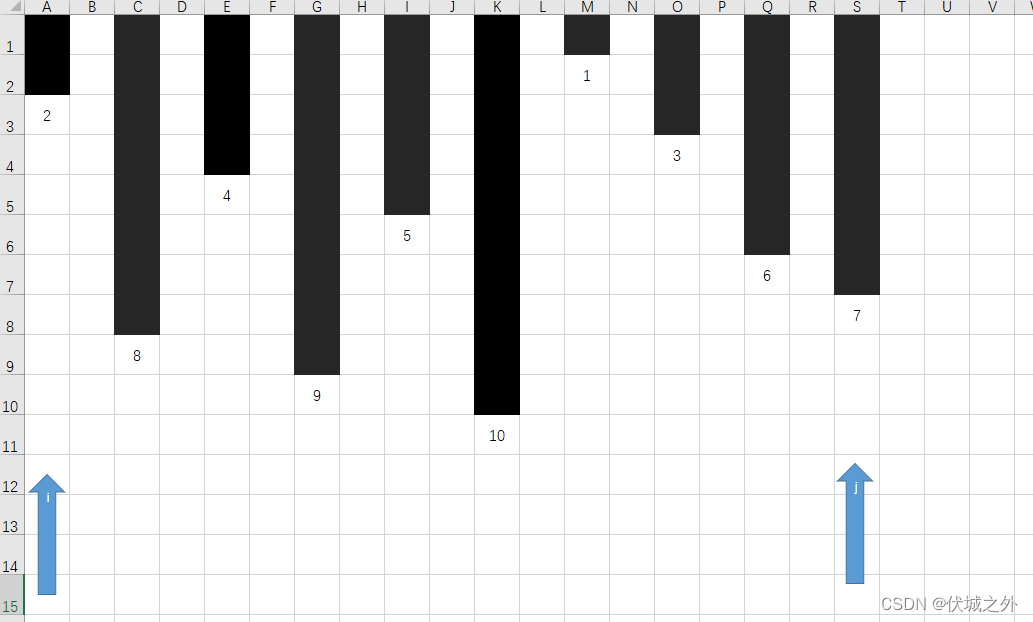
如果arr[]i < arr[j],则此时arr[i]是矮柱,arr[j]是高柱,则对于arr[i]来说,它作为矮柱的最大面积就是(j-i) * arr[i],然后移动i指针到下一位(因为i=0矮柱的最大面积已经求解出来了)

此时arr[i] > arr[j],则arr[j]是矮柱,arr[i]是高柱,对于arr[j]来说,他作为矮柱的最大面积就是(j-i)* arr[j],然后移动j指针到下一位(因为j=arr.length-1矮柱的最大面积已经求解出来了)
以此逻辑往复,直到ij相遇。这个过程中,始终是寻找矮柱,求出固定矮柱的最大面积。
上面逻辑的时间复杂度是O(n)
2023.06.11
Java语言,本题最后要求的最大太阳能板面积可能发生整型溢出,因此建议选用long。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const arr = line.split(",").map((ele) => parseInt(ele));
console.log(getMaxArea(arr));
});
function getMaxArea(arr) {
let i = 0;
let j = arr.length - 1;
let maxArea = 0;
while (i < j) {
let x = j - i; // 高柱~矮柱之间的距离
let y = arr[i] < arr[j] ? arr[i++] : arr[j--]; // 矮柱高度,并移动柱子
maxArea = Math.max(maxArea, x * y);
}
return maxArea;
}Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] heights = Arrays.stream(sc.nextLine().split(",")).mapToInt(Integer::parseInt).toArray();
System.out.println(getResult(heights));
}
public static long getResult(int[] heights) {
int l = 0;
int r = heights.length - 1;
long maxArea = 0;
while (l < r) {
long x = r - l;
long y = heights[l] < heights[r] ? heights[l++] : heights[r--];
maxArea = Math.max(maxArea, x * y);
}
return maxArea;
}
}
Python算法源码
# 输入获取
heights = list(map(int, input().split(",")))
# 算法入口
def getResult():
l = 0
r = len(heights) - 1
maxArea = 0
while l < r:
x = r - l
y = 0
if heights[l] < heights[r]:
y = heights[l]
l += 1
else:
y = heights[r]
r -= 1
maxArea = max(maxArea, x * y)
return maxArea
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#define MAX(a,b) ((a) > (b) ? (a) : (b))
#define MAX_SIZE 10000
int main() {
int heights[MAX_SIZE];
int heights_size = 0;
while(scanf("%d", &heights[heights_size++])) {
if(getchar() != ',') break;
}
int l = 0;
int r = heights_size - 1;
long maxArea = 0;
while(l < r) {
long x = r - l;
long y = heights[l] < heights[r] ? heights[l++] : heights[r--];
maxArea = MAX(maxArea, x * y);
}
printf("%ldn", maxArea);
return 0;
}免责声明:
评论0