目录
题目描述
给出数字K,请输出所有结果小于K的整数组合到一起的最少交换次数。
组合一起是指满足条件的数字相邻,不要求相邻后在数组中的位置。
数据范围:
-100 <= K <= 100
-100 <= 数组中数值 <= 100
输入描述
第一行输入数组:1 3 1 4 0
第二行输入K数值:2
输出描述
第一行输出最少交换次数:1
用例
| 输入 |
1 3 1 4 0 |
| 输出 | 1 |
| 说明 | 小于2的表达式是1 1 0, 共三种可能将所有符合要求数字组合一起,最少交换1次。 |
题目解析
这题是1151. 最少交换次数来组合所有的 1 – 力扣(LeetCode)
的变种题。解题可以使用滑动窗口。
我们首先需要统计 输入字符串1 3 1 4 0中 求出小于K的 整数的个数count,将其作为滑动窗口的长度。
滑动窗口的从左向右移动,每次移动一格,滑窗起点的移动范围是 [0 , arr.len – count],这样才能保证滑窗不越界。
每次移动后,统计滑动窗口内部 大于等于K的 元素的个数tmpSwapCount,而tmpSwapCount就是小于K的整数组合到一起需要交换次数。
比较每次移动的tmpSwapCount,求出最小的就是题解。
我们可以参考下面图示来理解上面逻辑,程序输入如下
1 6 3 9 8 4 2 5 7
6
含义是求解输入字符串中小于6的整数组合到一起需要的最少交换次数。
首先,我们求出输入字符串中有多少个小于6的整数,一共是5个,因此滑动窗口的长度就是5。
然后滑动窗口的起点移动范围是 [0, 4]
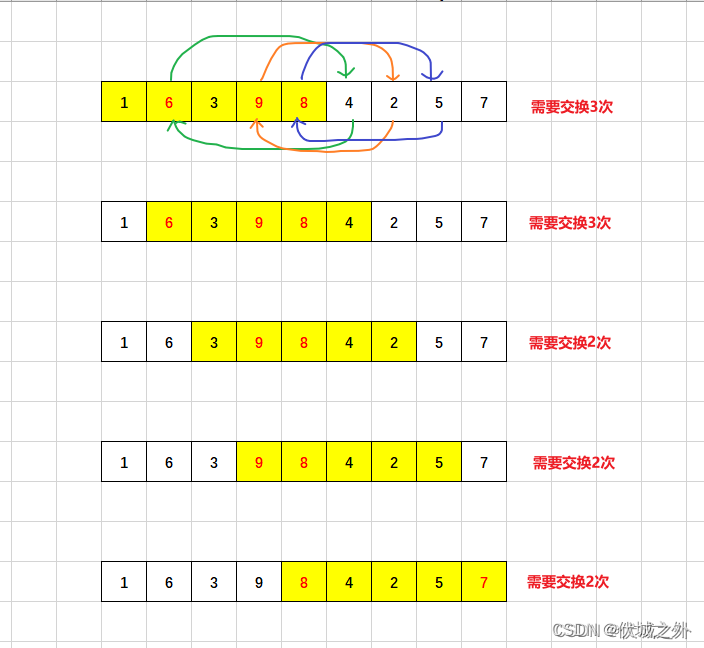
因此我们可以总结算法如下
function getMinSwapCount(arr, k) {
// 统计小于k的数组元素个数
let count = arr.reduce((pre, cur) => (cur < k ? pre + 1 : pre), 0);
let minSwapCount = count - 1; // 至多需要交换count-1次,就可以使小于k的整数组合在一起
let len = arr.length;
// 滑动窗口起始位置索引 i
for (let i = 0; i <= len - count; i++) {
// 当前滑动窗口内小于k的元素的个数,等价于使小于k的整数组合在一起需要的交换次数
let tmpSwapCount = 0;
// 滑动窗口长度为count,j 指向滑动窗口内每一个元素
for (let j = i; j < i + count; j++) {
if (arr[j] >= k) tmpSwapCount++;
}
// 比较谁是最少交换次数
minSwapCount = Math.min(minSwapCount, tmpSwapCount);
}
return minSwapCount;
}
console.log(getMinSwapCount([1, 6, 3, 9, 8, 4, 2, 5, 7], 6));
但是这种算法的时间复杂度差不多O(n^2),很容易超时,那么是不是存在可以优化的地方呢?
我们看下面图示
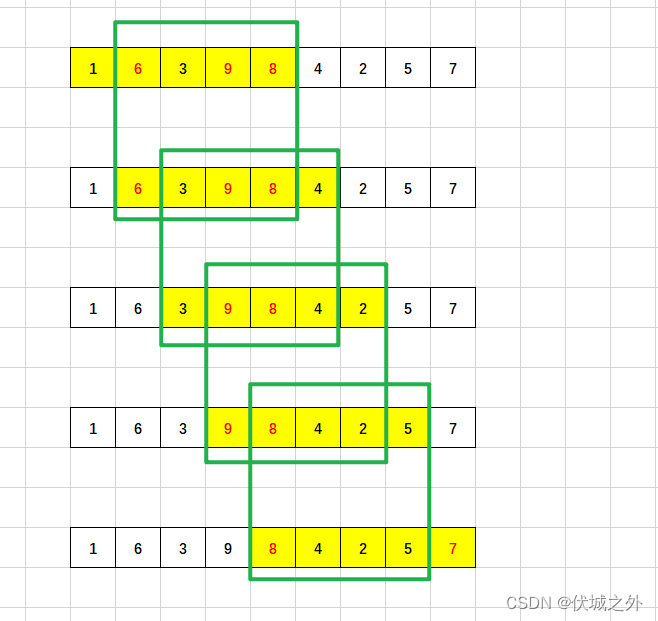
我们可以发现,上面那种算法,滑动窗口每次只移动一格,因此统计滑动窗口内部大于等于k的元素时,会和上次滑动窗口位置存在重复统计区域,如上图绿色框所示。
对于绿色框区域的元素,我们完全没有统计两次的必要,我们只需要统计滑动窗口每次移动后,失去的元素和新增的元素即可
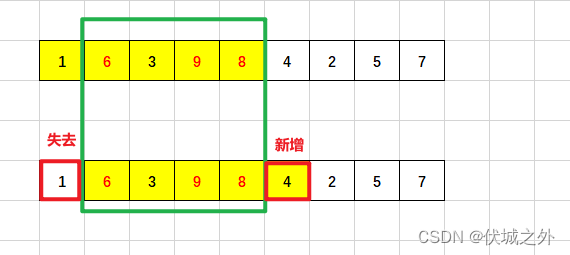
如上图中,当滑动窗口向右移动一格后,失去了元素1,新增了元素4,由于元素1<k,而元素4也<k,因此本次滑动窗口和上次滑动窗口需要的交换次数是相同的。即tmpSwapCount相同。
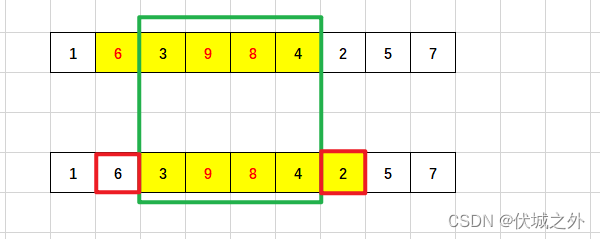
再看上图,滑动窗口移动一格后,失去了元素6,新增了元素2,而6>=k,2<k,因此本轮滑动窗口的tmpSwapCount–,比上一轮少了一次。
这种算法逻辑,我们只需要讲滑动窗口从左移动到右即可,即时间复杂度为O(n),算法源码如下
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] arr = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int k = Integer.parseInt(sc.nextLine());
System.out.println(getResult(arr, k));
}
public static int getResult(int[] arr, int k) {
// 统计小于k的数组元素个数
int count = 0;
for (int v : arr) if (v < k) count++;
// 如果只有1个小于k的元素,则不需要交换就能使小于k的元素组合在一起
if (count == 1) return 0;
// 先统计起点在0位置(即left=0)的滑动窗口的交换次数,得到一个minSwapCount初始值
int minSwapCount = 0;
for (int i = 0; i < count; i++) {
if (arr[i] >= k) minSwapCount++;
}
// 然后统计起点(left)在1~arr.length-count位置的滑动窗口的交换次数
// 可以转化为求解终点(right)在count~arr.length位置的滑动窗口的交换次数
int tmpSwapCount = minSwapCount;
for (int j = count; j < arr.length; j++) {
// 上一轮的left,即滑窗失去的元素的索引
int preLeft = j - count;
// j为滑窗新增的元素的索引
if (arr[preLeft] >= k && arr[j] < k) {
tmpSwapCount--;
} else if (arr[preLeft] < k && arr[j] >= k) {
tmpSwapCount++;
}
minSwapCount = Math.min(minSwapCount, tmpSwapCount);
}
return minSwapCount;
}
}
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
let arr = lines[0].split(" ").map(Number);
let k = parseInt(lines[1]);
console.log(getResult(arr, k));
lines.length = 0;
}
});
function getResult(arr, k) {
// 统计小于k的数组元素个数
let count = arr.reduce((pre, cur) => (cur < k ? pre + 1 : pre), 0);
// 如果只有1个小于k的元素,则不需要交换就能使小于k的元素组合在一起
if (count === 1) return 0;
// 先统计起点在0位置(即left=0)的滑动窗口的交换次数,得到一个minSwapCount初始值
let minSwapCount = 0;
for (let i = 0; i < count; i++) {
if (arr[i] >= k) {
minSwapCount++;
}
}
// 然后统计起点(left)在1~arr.length-count位置的滑动窗口的交换次数
// 可以转化为求解终点(right)在count~arr.length位置的滑动窗口的交换次数
let tmpSwapCount = minSwapCount;
for (let j = count; j < arr.length; j++) {
// 上一轮的left,即滑窗失去的元素的索引
let preLeft = j - count;
// 本轮的right,即滑窗新增的元素的索引
let curRight = j;
if (arr[preLeft] >= k && arr[curRight] < k) {
tmpSwapCount--;
} else if (arr[preLeft] < k && arr[curRight] >= k) {
tmpSwapCount++;
}
minSwapCount = Math.min(minSwapCount, tmpSwapCount);
}
return minSwapCount;
}
Python算法源码
# 输入获取
arr = list(map(int, input().split()))
k = int(input())
# 算法入口
def getResult():
# 统计小于k的数组元素个数
count = 0
for num in arr:
if num < k:
count += 1
# 如果只有1个小于k的元素,则不需要交换就能使小于k的元素组合在一起
if count == 1:
return 0
# 先统计起点在0位置(即left=0)的滑动窗口的交换次数,得到一个minSwapCount初始值
minSwapCount = 0
for i in range(count):
if arr[i] >= k:
minSwapCount += 1
# 然后统计起点(left)在1~arr.length-count位置的滑动窗口的交换次数
# 可以转化为求解终点(right)在count~arr.length位置的滑动窗口的交换次数
tmpSwapCount = minSwapCount
for j in range(count, len(arr)):
# 上一轮的left,即滑窗失去的元素的索引
preLeft = j - count
# j 为本轮滑窗新增的元素的索引
if arr[preLeft] >= k > arr[j]:
tmpSwapCount -= 1
elif arr[preLeft] < k <= arr[j]:
tmpSwapCount += 1
minSwapCount = min(minSwapCount, tmpSwapCount)
return minSwapCount
# 调用算法
print(getResult())
C算法源码
#include <stdio.h>
#define MIN(a,b) (a) < (b) ? (a) : (b)
#define MAX_SIZE 10000
int getResult(int arr[], int arr_size, int k);
int main() {
int arr[MAX_SIZE];
int arr_size = 0;
while(scanf("%d", &arr[arr_size++])) {
if(getchar() != ' ') break;
}
int k;
scanf("%d", &k);
printf("%dn", getResult(arr, arr_size, k));
return 0;
}
int getResult(int arr[], int arr_size, int k) {
int count = 0;
for(int i = 0; i < arr_size; i++) {
if(arr[i] < k) {
count++;
}
}
if(count == 1) return 0;
int minSwapCount = 0;
for(int i=0; i<count; i++) {
if(arr[i] >= k) minSwapCount++;
}
int tmpSwapCount = minSwapCount;
for(int j=count; j<arr_size; j++) {
int preLeft = j - count;
if(arr[preLeft] >= k && arr[j] < k) {
tmpSwapCount--;
} else if(arr[preLeft] < k && arr[j] >= k) {
tmpSwapCount++;
}
minSwapCount = MIN(minSwapCount, tmpSwapCount);
}
return minSwapCount;
}
免责声明:
评论0