题目描述
输入N个互不相同的二维整数坐标,求这N个坐标可以构成的正方形数量。[内积为零的的两个向量垂直]
输入描述
第一行输入为N,N代表坐标数量,N为正整数。N <= 100
之后的 K 行输入为坐标x y以空格分隔,x,y为整数,-10<=x, y<=10
输出描述
输出可以构成的正方形数量。
用例
| 输入 |
3 |
| 输出 | 0 (3个点不足以构成正方形) |
| 说明 | 无 |
| 输入 |
4 |
| 输出 | 1 |
| 说明 | 无 |
题目解析
其实当我们知道正方形相邻两点的坐标,即某条边的坐标后,就可以求出其余两点的坐标。
如下图中,我们知道正方形的红色点坐标后,就画出绿色点坐标和橙色点坐标来形成两个正方形,这其中似乎隐藏着什么规律?
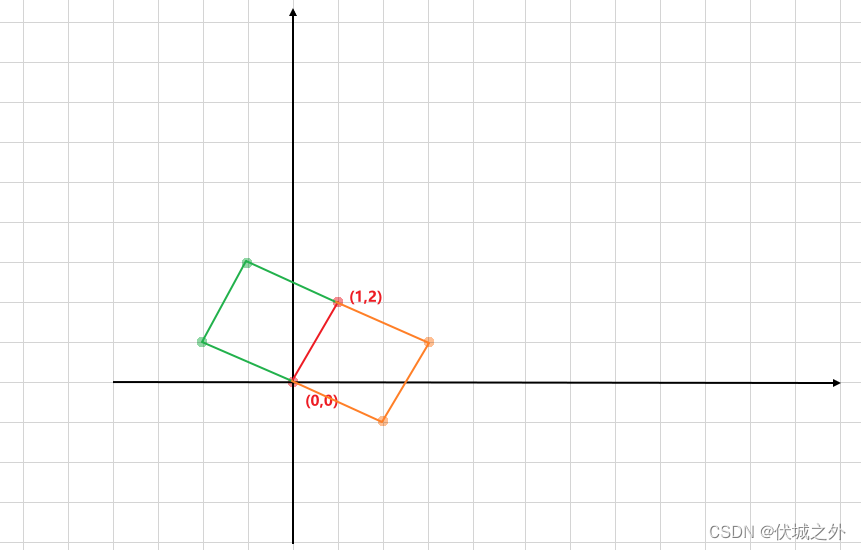
我们选取其中一个正方形来分析
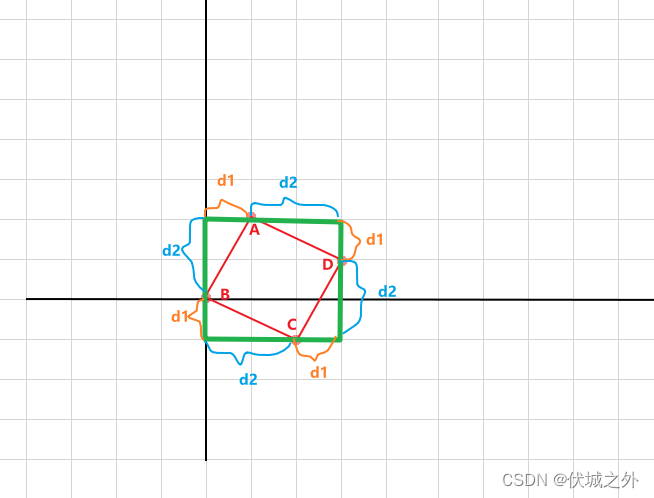
我们在目标正方形外面包裹一个更大的正方形,此时可以发现大正方形和小正方形相交点切割出了相同的几个尺寸:d1和d2。
假设已知A点坐标(x1, y1),B点坐标(x2,y2),那么
- d1 = x1 – x2
- d2 = y1 – y2
其实很容易可以发现,d1含义是A,B两点横向距离,d2是A,B两点纵向距离。
基于A,B点坐标,以及d1,d2,我们可以算出C,D点坐标分别为:
- C坐标 (x2 + d2, y2 – d1)
- D坐标 (x1 + d2, y1 – d1)
继续转化一下可得:
- C坐标 (x2 + y1 – y2, y2 – (x1 – x2))
- D坐标 (x1 + y1 – y2, y1 – (x1 – x2))
这是求A,B右下方向C,D边得公式推导。
同理,可以根据A,B推导出其左上方向E,F边,图示如下:
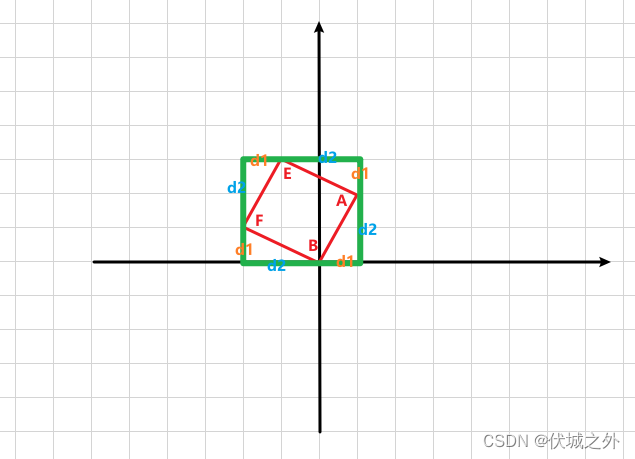
基于A,B点坐标,以及d1,d2,我们可以算出E,F点坐标分别为:
- E坐标 (x1 – d2,y1 + d1)
- F坐标 (x2 – d2,y1 + d1)
继续转化一下可得:
- E坐标 (x1 – (y1 – y2),y1 + x1 – x2)
- F坐标 (x2 – (y1 – y2),y1 + x1 – x2)
此时我们就得到了根据正方形任意相邻两点坐标,求另外两点坐标的公式了。
因此,接下来我们只需要遍历出两个点,然后通过公式得出另外可能的两个点,再在所有点中查找是否存在可能的两点,若存在,则正方形count++。
最后的正方形个数squareCount 需要除以 4,原因是,如果输入中真的存在如下图中的绿色,橙色点,则遍历过程中也会将绿色,橙色点遍历出来,然后求它们的可能正方形

也就是说上图中两个正方形,不仅会被两个红色点求出来两次次,还会被两个绿色点求出来一次,还会被两个橙色点求出来一次,还会被一绿一红求出来两次,被一橙一红求出来两次 ,总共是8次,而实际上只有2个正方形,因此最终结果要除以4。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
n = parseInt(lines[0]);
}
if (n && lines.length === n + 1) {
lines.shift();
console.log(getSquareCount(lines));
lines.length = 0;
}
});
/* 数学公式验证正方形 */
function getSquareCount(coordinates) {
let squareCount = 0;
const set = new Set(coordinates);
for (let i = 0; i < coordinates.length; i++) {
let [x1, y1] = coordinates[i].split(" ").map((ele) => parseInt(ele));
for (let j = i + 1; j < coordinates.length; j++) {
let [x2, y2] = coordinates[j].split(" ").map((ele) => parseInt(ele));
let x3 = x1 - (y1 - y2);
let y3 = y1 + (x1 - x2);
let x4 = x2 - (y1 - y2);
let y4 = y2 + (x1 - x2);
if (set.has(x3 + " " + y3) && set.has(x4 + " " + y4)) squareCount++;
let x5 = x1 + (y1 - y2);
let y5 = y1 - (x1 - x2);
let x6 = x2 + (y1 - y2);
let y6 = y2 - (x1 - x2);
if (set.has(x5 + " " + y5) && set.has(x6 + " " + y6)) squareCount++;
}
}
return squareCount / 4;
}
Java算法源码
import java.util.Arrays;
import java.util.HashSet;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
String[] coordinates = new String[n];
for (int i = 0; i < n; i++) {
coordinates[i] = sc.nextLine();
}
System.out.println(getResult(n, coordinates));
}
public static int getResult(int n, String[] coordinates) {
int squareCount = 0;
HashSet<String> set = new HashSet<>(Arrays.asList(coordinates));
for (int i = 0; i < n; i++) {
Integer[] arr1 =
Arrays.stream(coordinates[i].split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
int x1 = arr1[0], y1 = arr1[1];
for (int j = i + 1; j < n; j++) {
Integer[] arr2 =
Arrays.stream(coordinates[j].split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
int x2 = arr2[0], y2 = arr2[1];
int x3 = x1 - (y1 - y2), y3 = y1 + (x1 - x2);
int x4 = x2 - (y1 - y2), y4 = y2 + (x1 - x2);
if (set.contains(x3 + " " + y3) && set.contains(x4 + " " + y4)) squareCount++;
int x5 = x1 + (y1 - y2), y5 = y1 - (x1 - x2);
int x6 = x2 + (y1 - y2), y6 = y2 - (x1 - x2);
if (set.contains(x5 + " " + y5) && set.contains(x6 + " " + y6)) squareCount++;
}
}
return squareCount / 4;
}
}
Python算法源码
# 输入获取
n = int(input())
coordinates = [input() for _ in range(n)]
# 算法入口
def getResult():
squareCount = 0
coordinatesSet = set(coordinates)
for i in range(n):
x1, y1 = map(int, coordinates[i].split())
for j in range(i + 1, n):
x2, y2 = map(int, coordinates[j].split())
x3 = x1 - (y1 - y2)
y3 = y1 + (x1 - x2)
x4 = x2 - (y1 - y2)
y4 = y2 + (x1 - x2)
if f"{x3} {y3}" in coordinatesSet and f"{x4} {y4}" in coordinatesSet:
squareCount += 1
x5 = x1 + (y1 - y2)
y5 = y1 - (x1 - x2)
x6 = x2 + (y1 - y2)
y6 = y2 - (x1 - x2)
if f"{x5} {y5}" in coordinatesSet and f"{x6} {y6}" in coordinatesSet:
squareCount += 1
return squareCount // 4
# 算法调用
print(getResult())
免责声明:
评论0