题目描述
篮球(5V5)比赛中,每个球员拥有一个战斗力,每个队伍的所有球员战斗力之和为该队伍的总体战斗力。
现有10个球员准备分为两队进行训练赛,教练希望2个队伍的战斗力差值能够尽可能的小,以达到最佳训练效果。
给出10个球员的战斗力,如果你是教练,你该如何分队,才能达到最佳训练效果?请说出该分队方案下的最小战斗力差值。
输入描述
10个篮球队员的战斗力(整数,范围[1,10000]),战斗力之间用空格分隔,如:10987654321
不需要考虑异常输入的场景。
输出描述
最小的战斗力差值,如:1
用例
| 输入 | 10 9 8 7 6 5 4 3 2 1 |
| 输出 | 1 |
| 说明 | 1 2 5 9 10分为一队,3 4 6 7 8分为一队,两队战斗力之差最小,输出差值1。备注:球员分队方案不唯一,但最小战斗力差值固定是1 |
题目解析
本题由于只有十个数,并且平均分为两队,即每队五个数,因此只需要在10个数中选5个数组合即可模拟一队能力值。
有了一队的能力值之和A,我们用十个数的总和减去A,即得到了另一队的能力值之和B,最后求解Math.abs(A-B),即为两队能力值之差。
因此,有多少个10选5组合,就有多少组能力值之差,我们取其中最小的即为题解。
2023.08.21
组合问题的求解,可以想象成一颗树的遍历,比如原始数组array 为 [a,b,c,d],我们需要从中任选3个值组合,则可以得到树结构如下
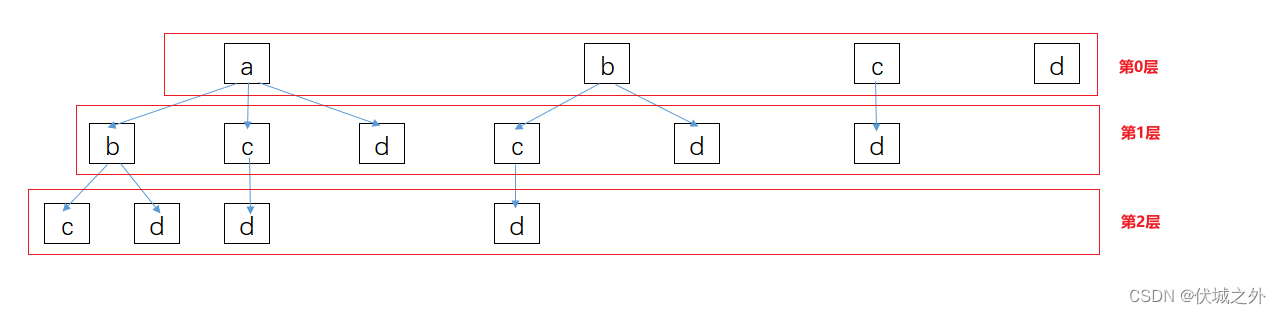
可以发现,组合内元素个数,其实就是树的层数。
树的每一层的元素选取规则如下:
如果第0层(即组合内第一个元素)的值选择a,那么第1层只能从原始数组的元素a后面的元素[b,c,d]中选取
如果第0层(即组合内第一个元素)的值选择b,那么第1层只能从原始数组的元素b后面的元素[c,d]中选取
注意如果第0层选择b,那么第1层再从原始数组中回头选元素b前面的a,否则会产生组合[b,a]
组合和排列不同,排列是在乎顺序的,即[a,b]和[b,a]是不同的排列,但是,组合不在意顺序,即[a,b]和[b,a]是相同组合。
找到树结构和组合的对应关系后,我们要求的组合,其实就是树的每一条分支,因此我们只要遍历树的每一个分支,其实就得到了每一个组合。
而树的分支遍历,最常用的方法其实就是回溯算法中的深度优先搜索。
但是,深度优先搜索遍历树,其实是一种纯暴力解法,遇到大数量级非常可能超时,或者Stack Overflow,因此我们需要进行剪枝优化。
所谓剪枝优化,其实就是将一些不必要的分支剪掉,比如上图中,我们可以看到某些分支的层数明显不足3层,因此对于这些分支,我们不需要进行遍历

组合求解,还有一个常用场景,那就是去重组合求解,比如原始数组为[a, a, b, b],从中任选3个数形成组合,则得到树结构如下

此时,我们可以发现,其中存在一些相同的组合
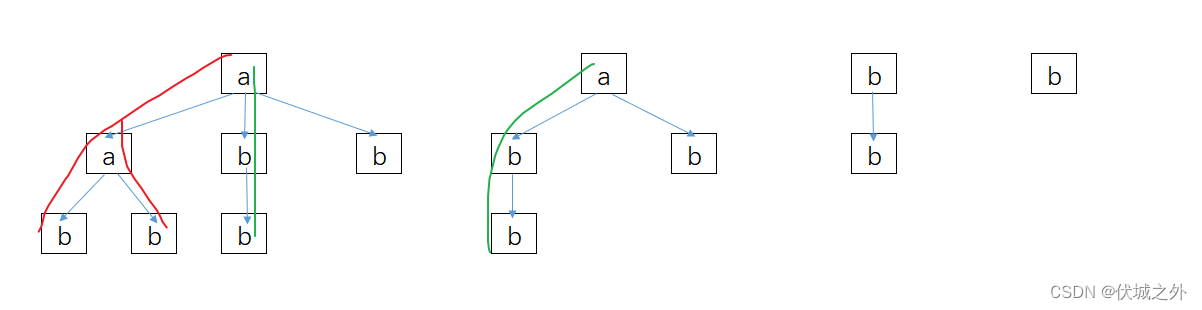
比如组合[a,a,b]有两个,组合[a,b,b]有两个
注意,这里的重复组合,不是由于元素回头选产生的,我们可以将上图中元素值,换成元素索引来看,此时从索引形成的组合来看,是不相同的。
那么如何高效的进行组合去重呢?
最高效的方式,是利用树中同一层的相邻元素关系,来进行剪枝

比如上图,第0层中,有两个相邻的a元素,那么就必然会产生重复的组合。
为什么呢?我们假设第一个a是a0,第二个a是a1,那么
- 如果第0层选择a0,那么第1层可以选a1,b,b
- 如果第1层选择a1,那么第2层可以选b,b
我们可以发现,“a0的下一层元素选取范围” 包含了 “a1的下一层元素选取范围”bi,因此必然会产生重复组合。
因此,如果我们当前要选取第level层的第i个元素时,可以检查它是否与第level层上一次选取的元素,即第i-1个元素(和第i个元素相邻)是否相同,如果相同,则可以剪枝。
这里需要特别注意的是,必须是同一层的相邻元素。
那么如何判断相邻元素是否处于同一层呢?
下图树中节点都是原始数组的元素的索引值
如上图所示,
第0层,从array的第0个索引元素开始选取,也就是说0~3索引范围元素处于第0层
第1层,从array的第1个索引元素开始选取,也就是说1~3索引范围元素处于第1层
第2层,从array的第2个索引元素开始选取,也就是说2~3索引范围元素处于第2层
那么,我们是否可以认为:第level层,从array的第level个索引元素开始选取,level~array.length-1索引范围元素处于第level层呢?
答案是不对的。
从上图的每一层来看,确实符合上面总结的规律,但是我们单看某个局部的话,如下图
按照上面规律,第1层元素从array的第1个索引元素开始选取,也就是说1~3索引范围元素处于第1层,
那么,符合上面红框处的情况吗?我们可以明显发现 索引1元素 和 索引2元素 处于不同层。
因此,更佳准确的规律是,假设某个组合的第level层,是从原数组的第index索引位置开始选取,那么对于 index ~ array.length-1 索引范围的元素 是处于同一层的。
那么,假设当前层的从原数组第index索引位置开始选取,因此 i 和 i-1 这两个相邻索引位置,想要处于同一层,则必须满足 i – 1 >= index && i >= index,即 i > index
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const arr = line.split(" ").map(Number);
console.log(getResult(arr));
});
function getResult(arr) {
arr.sort((a, b) => a - b);
const res = [];
// dfs求10选5的去重组合,并将组合之和记录进res中,即res中记录的是所有可能性的5人小队实力值之和
dfs(arr, 0, 0, 0, res);
const sum = arr.reduce((p, c) => p + c);
// 某队实力为subSum,则另一队实力为sum - subSum,则两队实力差为 abs((sum - subSum) - subSum),先求最小实力差
return res
.map((subSum) => Math.abs(sum - 2 * subSum))
.sort((a, b) => a - b)[0];
}
// 求解去重组合
function dfs(arr, index, level, sum, res) {
if (level === 5) {
return res.push(sum);
}
for (let i = index; i < 10; i++) {
if (i > index && arr[i] == arr[i - 1]) continue; // arr已经升序,这里进行树层去重
dfs(arr, i + 1, level + 1, sum + arr[i], res);
}
}
Java算法源码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] arr = new int[10];
for (int i = 0; i < 10; i++) {
arr[i] = sc.nextInt();
}
System.out.println(getResult(arr));
}
public static int getResult(int[] arr) {
Arrays.sort(arr);
ArrayList<Integer> res = new ArrayList<>();
// dfs求10选5的去重组合,并将组合之和记录进res中,即res中记录的是所有可能性的5人小队实力值之和
dfs(arr, 0, 0, 0, res);
int sum = Arrays.stream(arr).reduce(Integer::sum).orElse(0);
// 某队实力为subSum,则另一队实力为sum - subSum,则两队实力差为 abs((sum - subSum) - subSum),先求最小实力差
return res.stream().map(subSum -> Math.abs(sum - 2 * subSum)).min((a, b) -> a - b).orElse(0);
}
// 求解去重组合
public static void dfs(int[] arr, int index, int level, int sum, ArrayList<Integer> res) {
if (level == 5) {
res.add(sum);
return;
}
for (int i = index; i < 10; i++) {
if (i > index && arr[i] == arr[i - 1]) continue; // arr已经升序,这里进行树层去重
dfs(arr, i + 1, level + 1, sum + arr[i], res);
}
}
}
Python算法源码
# 输入获取
arr = list(map(int, input().split()))
# 求解去重组合
def dfs(arr, index, level, sumV, res):
if level == 5:
res.append(sumV)
return
for i in range(index, 10):
if i > index and arr[i] == arr[i - 1]: # arr已经升序,这里进行树层去重
continue
dfs(arr, i + 1, level + 1, sumV + arr[i], res)
# 算法入口
def getResult(arr):
arr.sort()
res = []
# dfs求10选5的去重组合,并将组合之和记录进res中,即res中记录的是所有可能性的5人小队实力值之和
dfs(arr, 0, 0, 0, res)
sumV = sum(arr)
# 某队实力为subSum,则另一队实力为sum - subSum,则两队实力差为 abs((sum - subSum) - subSum),先求最小实力差
return min(map(lambda subSum: abs(sumV - 2 * subSum), res))
# 算法调用
print(getResult(arr))
C算法源码
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define MIN(a,b) (a) < (b) ? (a) : (b)
typedef struct ListNode {
int ele;
struct ListNode *next;
} ListNode;
typedef struct LinkedList {
int size;
ListNode *head;
ListNode *tail;
} LinkedList;
LinkedList *new_LinkedList();
void addLast_LinkedList(LinkedList *link, int ele);
void dfs(int arr[], int index, int level, int sum, LinkedList *res);
int getResult(int arr[]);
int main() {
int arr[10];
for (int i = 0; i < 10; i++) {
scanf("%d", &arr[i]);
}
printf("%dn", getResult(arr));
return 0;
}
int cmp(const void *a, const void *b) {
return (*(int *) a) - (*(int *) b);
}
int getResult(int arr[]) {
qsort(arr, 10, sizeof(int), cmp);
LinkedList *res = new_LinkedList();
// dfs求10选5的去重组合,并将组合之和记录进res中,即res中记录的是所有可能性的5人小队实力值之和
dfs(arr, 0, 0, 0, res);
int sum = 0;
for (int i = 0; i < 10; i++) sum += arr[i];
int ans = INT_MAX;
// 某队实力为subSum,则另一队实力为sum - subSum,则两队实力差为 abs((sum - subSum) - subSum),先求最小实力差
ListNode *cur = res->head;
while (cur != NULL) {
ans = MIN(ans, abs(sum - 2 * cur->ele));
cur = cur->next;
}
return ans;
}
// 求解去重组合
void dfs(int arr[], int index, int level, int sum, LinkedList *res) {
if (level == 5) {
addLast_LinkedList(res, sum);
return;
}
for (int i = index; i < 10; i++) {
if (i > index && arr[i] == arr[i - 1]) continue; // arr已经升序,这里进行树层去重
dfs(arr, i + 1, level + 1, sum + arr[i], res);
}
}
LinkedList *new_LinkedList() {
LinkedList *link = (LinkedList *) malloc(sizeof(LinkedList));
link->size = 0;
link->head = NULL;
link->tail = NULL;
return link;
}
void addLast_LinkedList(LinkedList *link, int ele) {
ListNode *node = (ListNode *) malloc(sizeof(ListNode));
node->ele = ele;
node->next = NULL;
if (link->size == 0) {
link->head = node;
link->tail = node;
} else {
link->tail->next = node;
link->tail = node;
}
link->size++;
}
免责声明:



评论0