题目描述
DVD机在视频输出时,为了保护电视显像管,在待机状态会显示“屏保动画”,如下图所示,DVD Logo在屏幕内来回运动,碰到边缘会反弹。

请根据如下要求,实现屏保Logo坐标的计算算法。
- 屏幕是一个800*600像素的矩形,规定屏幕的左上角点坐标原点,沿横边向右方向为X轴,沿竖边向下方向为Y轴
- Logo是一个50*25像素的矩形,初始状态下,左上角点坐标记做(x,y),它在X和Y方向上均以1像素/秒的速度开始运动
- 遇到屏幕四个边缘后,会发生镜面反弹,即以45°碰撞边缘,再改变方向以45°弹出
- 当Logo和四个角碰撞时,两个边缘同时反弹的效果是Logo会原路返回

请编码实现,t秒后Logo左上角点的坐标。
输入描述
输入3个数字,以空格分隔:
x y t
第一个数字表示Logo左上角点的初始X坐标;
第二个数字表示Logo左上角点的初始Y坐标;
第三个数字表示时间 t,题目要求即求 t 秒后Logo左上角点的位置。
输出描述
输出2个数字,以空格分隔:
x y
第一个数字表示 t 秒后,Logo左上角点的X坐标
第二个数字表示 t 秒后,Logo左上角点的Y坐标
备注
所有用例均保证:
- 输入的x和y坐标会保证整个Logo都在屏幕范围内,Logo不会出画;
- 所有输入数据都是合法的数值,且不会出现负数;
- t 的最大值为100000。
用例
| 输入 | 0 0 10 |
| 输出 | 10 10 |
| 说明 | 输入样例表示Logo初始位置在屏幕的左上角点,10s后,Logo在X和Y方向都移动了10像素,因此输出10 10。 |
| 输入 | 500 570 10 |
| 输出 | 510 570 |
| 说明 | 输入样例表示初始状态下,Logo的下边缘再有5像素就碰到屏幕下边缘了,5s后,会与屏幕碰撞,碰撞后,斜向45弹出,又经过5s后,Logo与起始位置相比,水平移动了10像素,垂直方向回到了原来的高度。 |
题目解析
这道题其实可以转化为一个简单的物理常识题,或者看出一个数学问题。
举个例子,有一束红外线,和一个水平放置的镜面,假设红外线以和水平镜面45°夹角的位置射向镜面,问红外线会如何反射,如下图
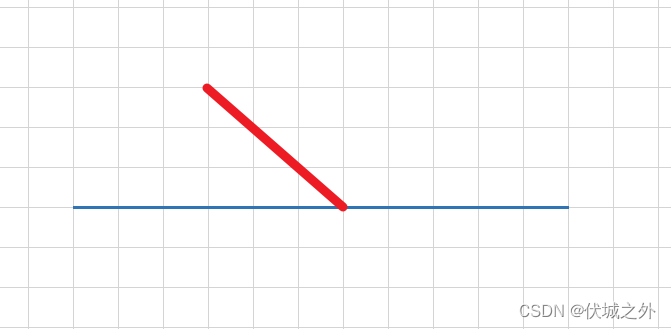
此时有两种策略,第一个策略是以红外线和镜面的交点开始,画一条与红外线呈90°夹角的线,这条线就是红外线的反射线

还有一个策略就是,让红外线穿透镜面后,沿着镜面对称反转

而本题就可以利用策略二思路解题。
得到x,y,t后,我们可以直接让
- x += t
- y += t
这其实就是相当于让红外线穿透镜面(如果t足够大)
之后,我们检查logo是否越界
- 若 x + 50 > 800,其中x + 50是logo的右下角横坐标,则说明越界,此时我们需要沿着x=800轴进行对称反转,反转后x+50坐标变为了 800 – (x+50 – 800),进而得到反转后 x = 800 – (x+50 – 800) – 50
- 若 y + 25 > 600,其中y + 25是logo的右下角纵坐标,则说明越界,此时我们y = 600轴进行对称反转,反转后y + 25坐标变为了 600 – (y+25 – 600),进而得到反转后 y = 600 – (y+25 – 600) – 25
当然除了上面logo越界情况,还有两个越界情况,如下:
- 若 x < 0,其中x是logo的左上角横坐标,则说明越界,此时我们需要沿着x=0轴进行对称反转,即反转后 x = -x
- 若 y < 0,其中y是logo的左上角纵坐标,则说明越界,此时我们需要沿着y=0轴进行对称反转,即反转后 y = -y
上面逻辑,大家可以对照下图思考一下

如果 t 足够大,则会进行多次越界反转逻辑,因此我们需要while循环判断反转后的x,y,x+50,y+25是否越界,如果越界则继续反转逻辑,否则就退出循环。
最后的x,y一定是不越界的,即最终坐标位置,此时可以作为题解返回。
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(getResult(sc.nextInt(), sc.nextInt(), sc.nextInt()));
}
public static String getResult(int x, int y, int t) {
x += t;
y += t;
while (y + 25 > 600 || y < 0 || x + 50 > 800 || x < 0) {
if (y + 25 > 600) {
// y = 600 - (y + 25 - 600) - 25;
y = 1150 - y;
}
if (x + 50 > 800) {
// x = 800 - (x + 50 - 800) - 50;
x = 1500 - x;
}
if (y < 0) {
y = -y;
}
if (x < 0) {
x = -x;
}
}
return x + " " + y;
}
}
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const [x, y, t] = line.split(" ").map(Number);
console.log(getResult(x, y, t));
});
function getResult(x, y, t) {
x += t;
y += t;
while (y + 25 > 600 || y < 0 || x + 50 > 800 || x < 0) {
if (y + 25 > 600) {
// y = 600 - (y + 25 - 600) - 25;
y = 1150 - y;
}
if (x + 50 > 800) {
// x = 800 - (x + 50 - 800) - 50;
x = 1500 - x;
}
if (y < 0) {
y = -y;
}
if (x < 0) {
x = -x;
}
}
return `${x} ${y}`;
}
Python算法源码
# 输入获取
x, y, t = list(map(int, input().split()))
# 算法入口
def getResult():
global x
global y
x += t
y += t
while y + 25 > 600 or y < 0 or x + 50 > 800 or x < 0:
if y + 25 > 600:
# y = 600 - (y + 25 - 600) - 25
y = 1150 - y
if x + 50 > 800:
# x = 800 - (x + 50 - 800) -50
x = 1500 - x
if y < 0:
y = -y
if x < 0:
x = -x
return f"{x} {y}"
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
int main()
{
int x, y, t;
scanf("%d %d %d", &x, &y, &t);
x += t;
y += t;
while(y + 25 > 600 || y < 0 || x + 50 > 800 || x < 0) {
if(y + 25 > 600) {
// y = 600 - (y + 25 - 600) - 25;
y = 1150 - y;
}
if(x + 50 > 800) {
// x = 800 - (x + 50 - 800) - 50;
x = 1500 - x;
}
if(y < 0) {
y = -y;
}
if(x < 0) {
x = -x;
}
}
printf("%d %dn", x, y);
return 0;
}
免责声明:
1、IT资源小站为非营利性网站,全站所有资料仅供网友个人学习使用,禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享,本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题,请立即告知本站,本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体,但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员,一律视为同意网站规定,本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0