题目描述
近些年来,我国防沙治沙取得显著成果。某沙漠新种植N棵胡杨(编号1-N),排成一排。
一个月后,有M棵胡杨未能成活。
现可补种胡杨K棵,请问如何补种(只能补种,不能新种),可以得到最多的连续胡杨树?
输入描述
N 总种植数量,1 <= N <= 100000
M 未成活胡杨数量,M 个空格分隔的数,按编号从小到大排列,1 <= M <= N
K 最多可以补种的数量,0 <= K <= M
输出描述
最多的连续胡杨棵树
用例
| 输入 |
5 |
| 输出 |
3 |
| 说明 | 补种到2或4结果一样,最多的连续胡杨棵树都是3。 |
| 输入 | 10 3 2 4 7 1 |
| 输出 | 6 |
| 说明 | 补种第7棵树,最多连续胡杨树棵数位6(5,6,7,8,9,10) |
双指针解法
这题感觉还是比较难的,按照用例意思,种了5棵树,我们用1代表活树,则:
1,1,1,1,1
然后死了2两棵树,分别是第2棵树、第4棵树,我们用0代表死树,则:
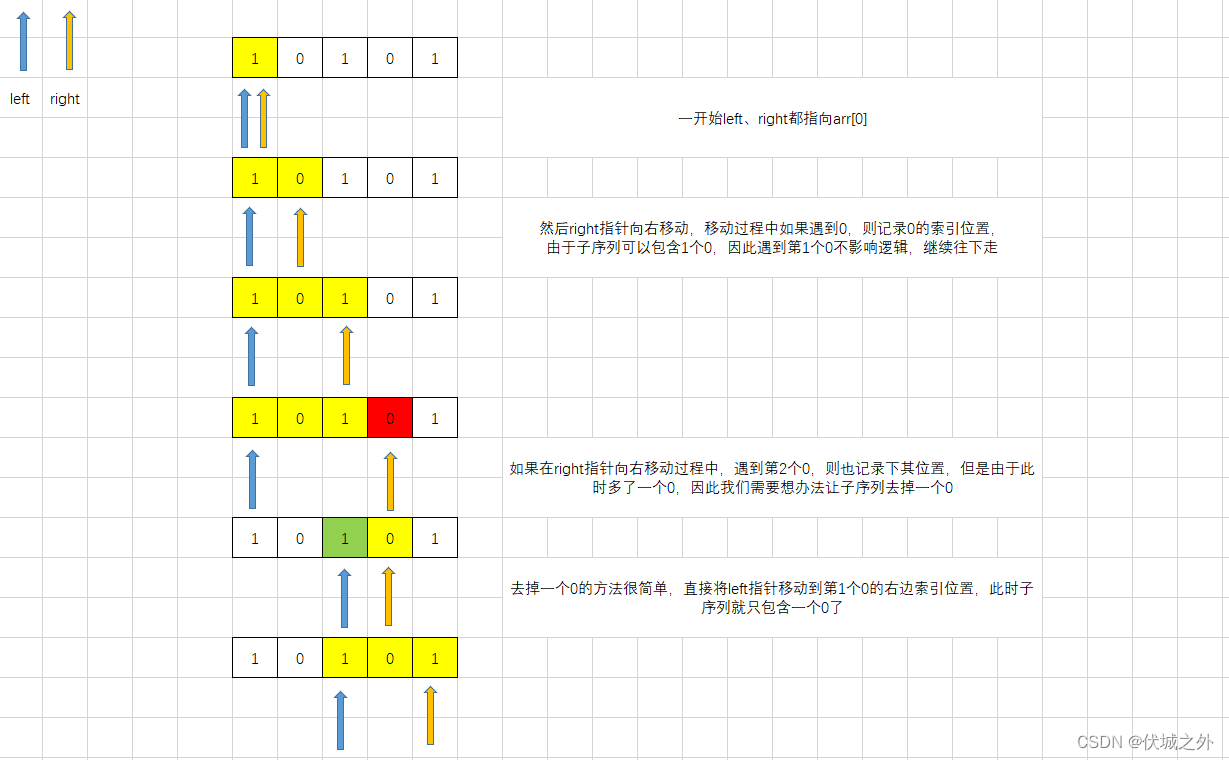
1,0,1,0,1
现在我们可以在死树位置,补种一颗活树,即可以将某个0替换为1,问,此时连续活树的最大长度?
转换一下问题,其实就是:
在1,0,1,0,1数列中,求包含一个0的最长子序列?
这其实是一个典型的滑动窗口问题,而滑动窗口的实现依赖于双指针,即两个指针之间的序列就是滑动窗口,我们只要保证滑动窗口内部只含1个0即可
我们在举一个例子,数列:1,0,0,0,1,可以补种2棵树
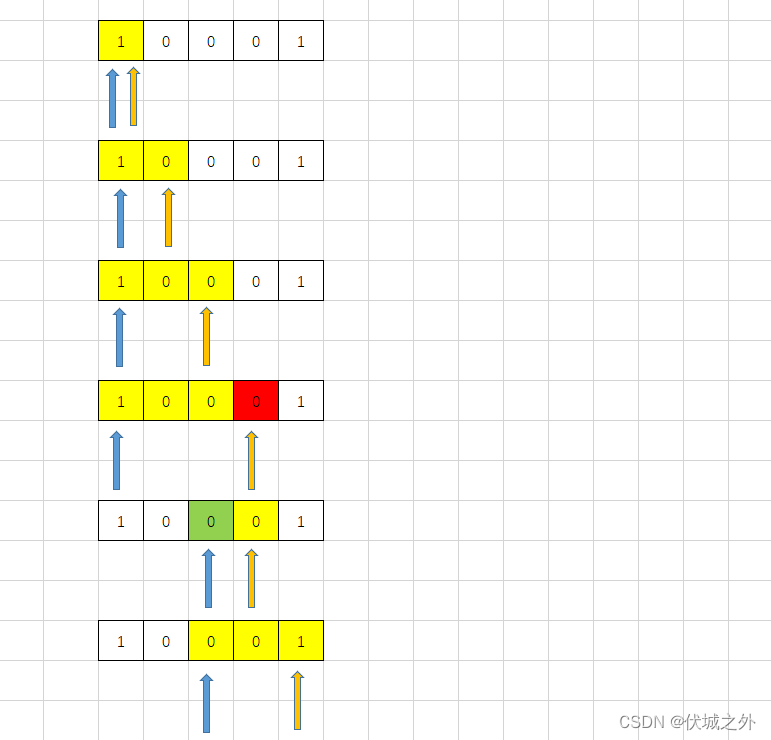
我们可以通过这两个例子发现,比较难的实现是left指针的移动,我们需要记录right指针每次扫描到0的索引,当滑动窗口内0超过制定数量时,我们可以抛弃记录的滑动窗口内部的第一个0及之前部分,因此即让left指针移动到记录的第一个0的右边。
下面源码实现中,我使用的occur来记录滑动窗口中0出现的索引位置,当0超标时,就occur.shift()弹出第一个0的索引位置index,然后让left = index + 1,即能起到帮助滑动窗口去除1个0的效果。
下面源码中,还有一个地方的实现可能会让大家产生疑问,那就是maxLen,即最长子序列长度的计算,我用了两种公式:
- maxLen = Math.max(maxLen, right – left);
- maxLen = Math.max(maxLen, right – left + 1);
第一个公式是当0超标时,最长子序列的长度计算,如下图

right = 3,left=0,此时滑动窗口长度为 right – left
第二个公式是0不超标时,最长子序列的长度计算,如下图

right = 2, left = 0,此时滑动窗口长度为 right – left + 1
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 4) {
let n = lines[0] - 0;
let m = lines[1] - 0;
let k = lines[3] - 0;
const arr = new Array(n).fill(1);
let idx = lines[2].split(" ").slice(0, m);
for (let i = 0; i < idx.length; i++) {
arr[idx[i] - 1] = 0;
}
console.log(slide(arr, k));
lines.length = 0;
}
});
/* 滑动窗口 */
function slide(arr, k) {
let left = 0;
let occur = [];
let maxLen = 0;
for (let right = 0; right < arr.length; right++) {
if (arr[right] === 0) {
occur.push(right);
if (occur.length > k) {
maxLen = Math.max(maxLen, right - left);
left = occur.shift() + 1;
continue;
}
}
maxLen = Math.max(maxLen, right - left + 1);
}
return maxLen;
}
Java算法源码
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[] arr = new int[n];
Arrays.fill(arr, 1);
for (int i = 0; i < m; i++) {
int deadIdx = sc.nextInt() - 1;
arr[deadIdx] = 0;
}
int k = sc.nextInt();
System.out.println(getResult(arr, k));
}
public static int getResult(int[] arr, int k) {
int left = 0;
LinkedList<Integer> occur = new LinkedList<>();
int maxLen = 0;
for (int right = 0; right < arr.length; right++) {
if (arr[right] == 0) {
occur.addLast(right);
if (occur.size() > k) {
maxLen = Math.max(maxLen, right - left);
left = occur.removeFirst() + 1;
continue;
}
}
maxLen = Math.max(maxLen, right - left + 1);
}
return maxLen;
}
}
Python算法源码
# 输入获取
n = int(input())
m = int(input())
deadIdx = list(map(int, input().split()))
arr = [1]*n
for i in range(m):
arr[deadIdx[i]-1] = 0
k = int(input())
# 算法入口
def getResult(arr, n, m, k):
left = 0
occur = []
maxLen = 0
for right in range(n):
if arr[right] == 0:
occur.append(right)
if len(occur) > k:
maxLen = max(maxLen, right - left)
left = occur.pop(0) + 1
continue
maxLen = max(maxLen, right - left + 1)
return maxLen
# 算法调用
print(getResult(arr, n, m, k))
C算法源码
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MAX(a,b) (a) > (b) ? (a) : (b)
typedef struct ListNode {
int ele;
struct ListNode* next;
} ListNode;
typedef struct LinkedList {
int size;
ListNode* head;
ListNode* tail;
} LinkedList;
LinkedList* new_LinkedList();
void addLast_LinkedList(LinkedList* link, int ele);
int removeFirst_LinkedList(LinkedList* link);
int getResult(int n, int arr[], int k);
int main() {
int n;
scanf("%d", &n);
int m;
scanf("%d", &m);
int arr[n];
for(int i=0; i<n; i++) {
arr[i] = 1;
}
for(int i=0; i<m; i++) {
int deadIdx;
scanf("%d", &deadIdx);
arr[deadIdx - 1] = 0;
}
int k;
scanf("%d", &k);
printf("%dn", getResult(n, arr, k));
return 0;
}
int getResult(int n, int arr[], int k) {
int left = 0;
LinkedList* occur = new_LinkedList();
int maxLen = 0;
for(int right = 0; right < n; right++) {
if(arr[right] == 0) {
addLast_LinkedList(occur, right);
if(occur->size > k) {
maxLen = MAX(maxLen, right - left);
left = removeFirst_LinkedList(occur) + 1;
continue;
}
}
maxLen = MAX(maxLen, right - left + 1);
}
return maxLen;
}
LinkedList* new_LinkedList() {
LinkedList* link = (LinkedList*) malloc(sizeof(LinkedList));
link->head = NULL;
link->tail = NULL;
link->size = 0;
return link;
}
void addLast_LinkedList(LinkedList* link, int ele) {
ListNode* node = (ListNode*) malloc(sizeof(ListNode));
node->ele = ele;
node->next = NULL;
if(link->size == 0) {
link->head = node;
link->tail = node;
} else {
link->tail->next = node;
link->tail = node;
}
link->size++;
}
int removeFirst_LinkedList(LinkedList* link) {
if(link->size == 0) exit(-1);
ListNode* removed = link->head;
if(link->size == 1) {
link->head = NULL;
link->tail = NULL;
} else {
link->head = link->head->next;
}
link->size--;
int res = removed->ele;
free(removed);
return res;
}单指针解法
前面的算法是基于双指针实现的滑动窗口,并且为了记录left指针的位置,还额外创建了一个occur数组来保存right指针扫描过程中遇到的0,但是实际输入的第三行就提供了死树的索引位置,如本题用例中的第三行输入的2 4,因此我们的occur数组算是一个冗余。
我们基于死树索引位置,以及补种k值,就可以得出left、right指针位置,即找出滑动窗口,逻辑如下:
我们用一个指针来从左到右遍历每一棵死树,死树用红色标记,如下图第一行
如果k=1的话,则滑动窗口只能包含遍历到的死树,不能包含其他死树,因此滑动窗口有如下三种情况
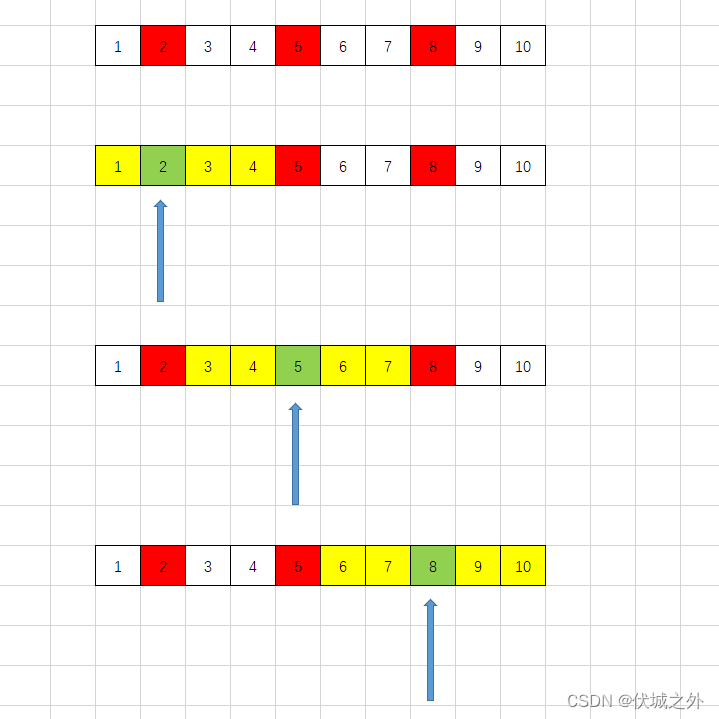
如果k=2,则情况如下

因此我们可以得出结论:
假设总树有n棵,死树有m棵,且死树索引保存在arr中,比如arr = [2,5,8],补种k棵。
则此时指向死树的单指针的移动范围在arr数组的 0 ~ m-k ,
而滑动窗口的范围在:
如果滑动窗口包含边界的话,即包含总树的开头或结尾,此时单指针的指向固定为:
- arr[0](包含开头),此时滑动窗口的长度为 arr[0+k] – 1,如下图所示
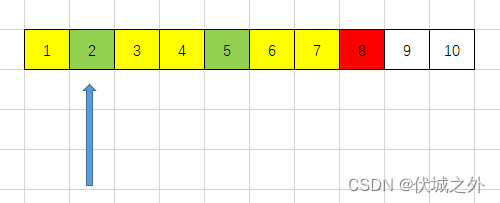
- arr[m-k](包含结尾),此时滑动窗口的长度为 n – arr[m-k-1] ,如下图所示

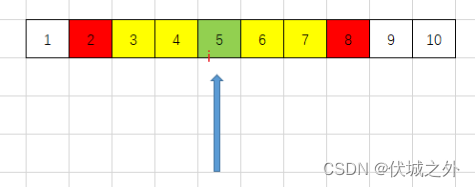
如果滑动窗口的范围不包含总树边界,即在中间位置,则滑动窗口的长度为 arr[i+k] – arr[i-1] – 1,如下图所示
2023.09.09
上面逻辑应该考虑下m == k的情况,即补种数 == 未成活数,此时可以直接返回n,即补种后所有树都成活了。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 4) {
let n = lines[0] - 0; // 一共多少颗树
let m = lines[1] - 0; // 死了多少棵树
let idx = lines[2]
.split(" ")
.slice(0, m)
.map((ele) => parseInt(ele)); // 死树的序号,从1开始
let k = lines[3] - 0; // 补种多少颗树
console.log(slide(n, m, idx, k));
lines.length = 0;
}
});
/**
* 滑动窗口
* @param {number} n 总共多少棵树
* @param {number} m 总共死了多少棵树
* @param {Array} idx 死树序号,从1开始
* @param {number} k 补种多少棵树
* @return {number} 连续最长活树的长度
*/
function slide(n, m, idx, k) {
if (m == k) {
return n;
}
let maxLen = 0;
for (let i = 0; i <= m - k; i++) {
if (i === 0) {
maxLen = Math.max(maxLen, idx[i + k] - 1);
} else if (i === m - k) {
maxLen = Math.max(maxLen, n - idx[i - 1]);
} else {
maxLen = Math.max(maxLen, idx[i + k] - idx[i - 1] - 1);
}
}
return maxLen;
}
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[] deadIdx = new int[m];
for (int i = 0; i < m; i++) {
deadIdx[i] = sc.nextInt();
}
int k = sc.nextInt();
System.out.println(getResult(n, m, deadIdx, k));
}
/**
* @param n 总共多少棵树
* @param m 总共死了多少棵树
* @param deadIdx 数组,元素是死树序号,从1开始
* @param k 补种多少棵树
* @return 连续最长活树的长度
*/
public static int getResult(int n, int m, int[] deadIdx, int k) {
if (m == k) return n;
int maxLen = 0;
for (int i = 0; i <= m - k; i++) {
if (i == 0) {
maxLen = Math.max(maxLen, deadIdx[i + k] - 1);
} else if (i == m - k) {
maxLen = Math.max(maxLen, n - deadIdx[i - 1]);
} else {
maxLen = Math.max(maxLen, deadIdx[i + k] - deadIdx[i - 1] - 1);
}
}
return maxLen;
}
}
Python算法源码
# 输入获取
n = int(input())
m = int(input())
deadIdx = list(map(int, input().split()))
k = int(input())
# 算法入口
def getResult(n, m, deadIdx, k):
if m == k:
return n
maxLen = 0
for i in range(m - k + 1):
if i == 0:
maxLen = max(maxLen, deadIdx[i + k] - 1)
elif i == m - k:
maxLen = max(maxLen, n - deadIdx[i - 1])
else:
maxLen = max(maxLen, deadIdx[i + k] - deadIdx[i - 1] - 1)
return maxLen
# 算法调用
print(getResult(n, m, deadIdx, k))C算法源码
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MAX(a,b) (a) > (b) ? (a) : (b)
int getResult(int n, int m, int deadIdx[], int k);
int main() {
int n;
scanf("%d", &n);
int m;
scanf("%d", &m);
int deadIdx[m];
for(int i=0; i<m; i++) {
scanf("%d", &deadIdx[i]);
}
int k;
scanf("%d", &k);
printf("%dn", getResult(n, m, deadIdx, k));
return 0;
}
int getResult(int n, int m, int deadIdx[], int k) {
if(m == k) return n;
int maxLen = 0;
for(int i=0; i<=m-k; i++) {
if(i == 0) {
maxLen = MAX(maxLen, deadIdx[i+k] - 1);
} else if(i == m - k) {
maxLen = MAX(maxLen, n - deadIdx[i-1]);
} else {
maxLen = MAX(maxLen, deadIdx[i+k] - deadIdx[i-1] - 1);
}
}
return maxLen;
}免责声明:
评论0