题目描述
某长方形停车场,每个车位上方都有对应监控器,当且仅当在当前车位或者前后左右四个方向任意一个车位范围停车时,监控器才需要打开;
给出某一时刻停车场的停车分布,请统计最少需要打开多少个监控器;
输入描述
第一行输入m,n表示长宽,满足1 < m,n <= 20;
后面输入m行,每行有n个0或1的整数,整数间使用一个空格隔开,表示该行已停车情况,其中0表示空位,1表示已停;
输出描述
最少需要打开监控器的数量;
用例
| 输入 | 3 3 0 0 0 0 1 0 0 0 0 |
| 输出 | 5 |
| 说明 | 无 |
题目解析
本题题意比较难以理解,但是画一幅图给大家看下就懂了
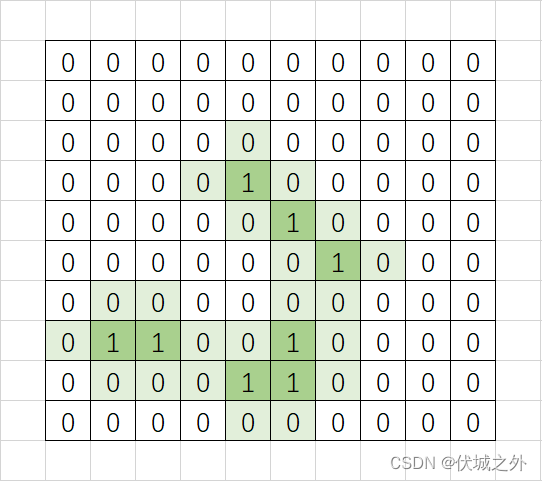
停车(1)的位置必须要打开监控器,另外停车位置的上下左右位置(1或0)的监控器也要打开,问最终需要打开多少个监控器?
即,求解上面图示种有颜色的格子数量。
解题思路如下:
遍历矩阵每一个元素,
- 如果元素值为1,对应位置的监控器就要打开。
- 如果元素值为0,则需要进一步检查其上下左右四个位置,只要这四个位置有一个元素值为1,则当前位置的监控器需要打开
JavaScript算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const [m, n] = (await readline()).split(" ").map(Number);
const matrix = [];
for (let i = 0; i < m; i++) {
matrix.push((await readline()).split(" ").map(Number));
}
console.log(getResult(matrix, m, n));
})();
function getResult(matrix, m, n) {
// 记录需要打开的监控器数量
let count = 0;
// 上下左右四个方向的偏移量
const offsets = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1],
];
for (let x = 0; x < m; x++) {
for (let y = 0; y < n; y++) {
// 如果元素值为1,对应位置的监控器就要打开
if (matrix[x][y] === 1) {
count++;
continue;
}
// 如果元素值为0,则需要进一步检查其上下左右4个位置,只要这四个位置有一个元素值为1,则当前位置的监控器需要打开
for (let [offsetX, offsetY] of offsets) {
const newX = x + offsetX;
const newY = y + offsetY;
if (
newX >= 0 &&
newX < m &&
newY >= 0 &&
newY < n &&
matrix[newX][newY] === 1
) {
count++;
break;
}
}
}
}
return count;
}
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int n = sc.nextInt();
int[][] matrix = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = sc.nextInt();
}
}
System.out.println(getResult(m, n, matrix));
}
public static int getResult(int m, int n, int[][] matrix) {
// 记录需要打开的监控器数量
int count = 0;
// 上下左右四个方向的偏移量
int[][] offsets = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
for (int x = 0; x < m; x++) {
for (int y = 0; y < n; y++) {
// 如果元素值为1,对应位置的监控器就要打开
if (matrix[x][y] == 1) {
count++;
continue;
}
// 如果元素值为0,则需要进一步检查其上下左右4个位置,只要这四个位置有一个元素值为1,则当前位置的监控器需要打开
for (int[] offset : offsets) {
int newX = x + offset[0];
int newY = y + offset[1];
if (newX >= 0 && newX < m && newY >= 0 && newY < n && matrix[newX][newY] == 1) {
count++;
break;
}
}
}
}
return count;
}
}
Python算法源码
# 输入获取
m, n = map(int, input().split())
matrix = [list(map(int, input().split())) for _ in range(m)]
# 算法入口
def getResult():
# 记录需要打开的监控器数量
count = 0
# 上下左右四个方向的偏移量
offsets = ((-1, 0), (1, 0), (0, -1), (0, 1))
for x in range(m):
for y in range(n):
# 如果元素值为1,对应位置的监控器就要打开
if matrix[x][y] == 1:
count += 1
continue
# 如果元素值为0,则需要进一步检查其上下左右4个位置,只要这四个位置有一个元素值为1,则当前位置的监控器需要打开
for offsetX, offsetY in offsets:
newX = x + offsetX
newY = y + offsetY
if m > newX >= 0 and n > newY >= 0 and matrix[newX][newY] == 1:
count += 1
break
return count
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#define MAX_ROWS 20
#define MAX_COLS 20
int main()
{
// 输入获取
int m, n;
scanf("%d %d", &m, &n);
int matrix[MAX_ROWS][MAX_COLS];
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
scanf("%d", &matrix[i][j]);
}
}
// 记录需要打开的监控器数量
int count = 0;
// 上下左右四个方向的偏移量
int offsets[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for(int x = 0; x < m; x++) {
for(int y = 0; y < n; y++) {
// 如果元素值为1,对应位置的监控器就要打开
if(matrix[x][y] == 1) {
count++;
continue;
}
// 如果元素值为0,则需要进一步检查其上下左右4个位置,只要这四个位置有一个元素值为1,则当前位置的监控器需要打开
for(int i = 0; i < 4; i++) {
int offsetX = offsets[i][0];
int offsetY = offsets[i][1];
int newX = x + offsetX;
int newY = y + offsetY;
if(newX >=0 && newX < m && newY >= 0 && newY < n && matrix[newX][newY] == 1) {
count++;
break;
}
}
}
}
// 输出打印
printf("%dn", count);
return 0;
}免责声明:
1、IT资源小站为非营利性网站,全站所有资料仅供网友个人学习使用,禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享,本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题,请立即告知本站,本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体,但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员,一律视为同意网站规定,本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0