题目描述
手上有一副扑克牌,每张牌按牌面数字记分(J=11,Q=12,K=13,没有大小王),出牌时按照以下规则记分:
- 出单张,记牌面分数,例如出一张2,得分为2
- 出对或3张,记牌面分数总和再x2,例如出3张3,得分为(3+3+3)x2=18
- 出5张顺,记牌面分数总和再x2,例如出34567顺,得分为(3+4+5+6+7)x2=50
- 出4张炸弹,记牌面分数总和再x3,例如出4张4,得分为4x4x3=48
求出一副牌最高的得分数
输入描述
按顺序排好的一副牌,最少1张,最多15张。
1-9输入为数字1-9,10输入为数字0,JQK输入为大写字母JQK.
无需考虑输入非法的情况,例如输入字符不在[0-9JQK]范围或某一张牌超过4张
输出描述
最高的得分数
备注
积分规则中没有的出牌方式不支持,例如不支持3带1、4带2,不支持5张以上的顺,且10JQKA (0JQK1) 不算顺。
用例
| 输入 | 33445677 |
| 输出 | 67 |
| 说明 |
出对3、对4、对7,单张5、6,得分为67; 出34567顺,再出单张3、4、7,得分为64 因此最高得分是按对出,可得到最高分67,输出结果67 |
题目解析
本题数量级不大,可以考虑暴力破解。
首先定义一个数组card_count,数组索引就是牌分数,数组元素就是牌数量
因为本题中牌面是不连续的,比如0代表10,但是牌分数是连续的。
因此,将牌分数作为数组索引来看的话,就可以用一个长度为5的滑窗来在card_count中找顺子。
由于K牌面分数是13,因此我们只需要定义card_count数组长度为14即可,题目用例可得数组如下:

有了card_count之后,我们就可以开始遍历每一种牌(即遍历card_count数组的索引 i ):
- card_count[i] >= 1,则说明当前牌面 i 至少有1张,那么此时可以选择:
- 出单张,那么总牌数量 – 1,总分 + i
- 出顺子,但是需要先检查 i+1, i+2, i+3, i+4 牌的数量是否至少有1张,如果有的话,才可以出顺子,那么总牌数了 – 5,总分+ ( i + (i+1) + (i+2) + (i+3) + (i+4) ) * 2
- card_count[i] >= 2,则说明当前牌面 i 至少有2张,那么此时可以选择出对子,总牌数量 – 2,总分 + i * 2 * 2
- card_count[i] >= 3,则说明当前牌面 i 至少有3张,那么此时可以选择出三张,总牌数量 – 3,总分 + i * 3 * 2
- card_count[i] >= 4,则说明当前牌面 i 至少有4张,那么此时可以选择出炸弹,总牌数量 – 4,总分 + i * 4 * 3
对于上面这些出牌策略,我们都可以选或者不选,
比如当前card_count[i] >= 2,那么我们可以选择出对子,也可以选择不出对子
只有这样,我们才能尝试出所有出牌的策略组合,这里明显需要用到递归和回溯。
2023.10.29
之前的代码逻辑中,如下(C语言代码,其他语言的考友可以当成伪代码看)
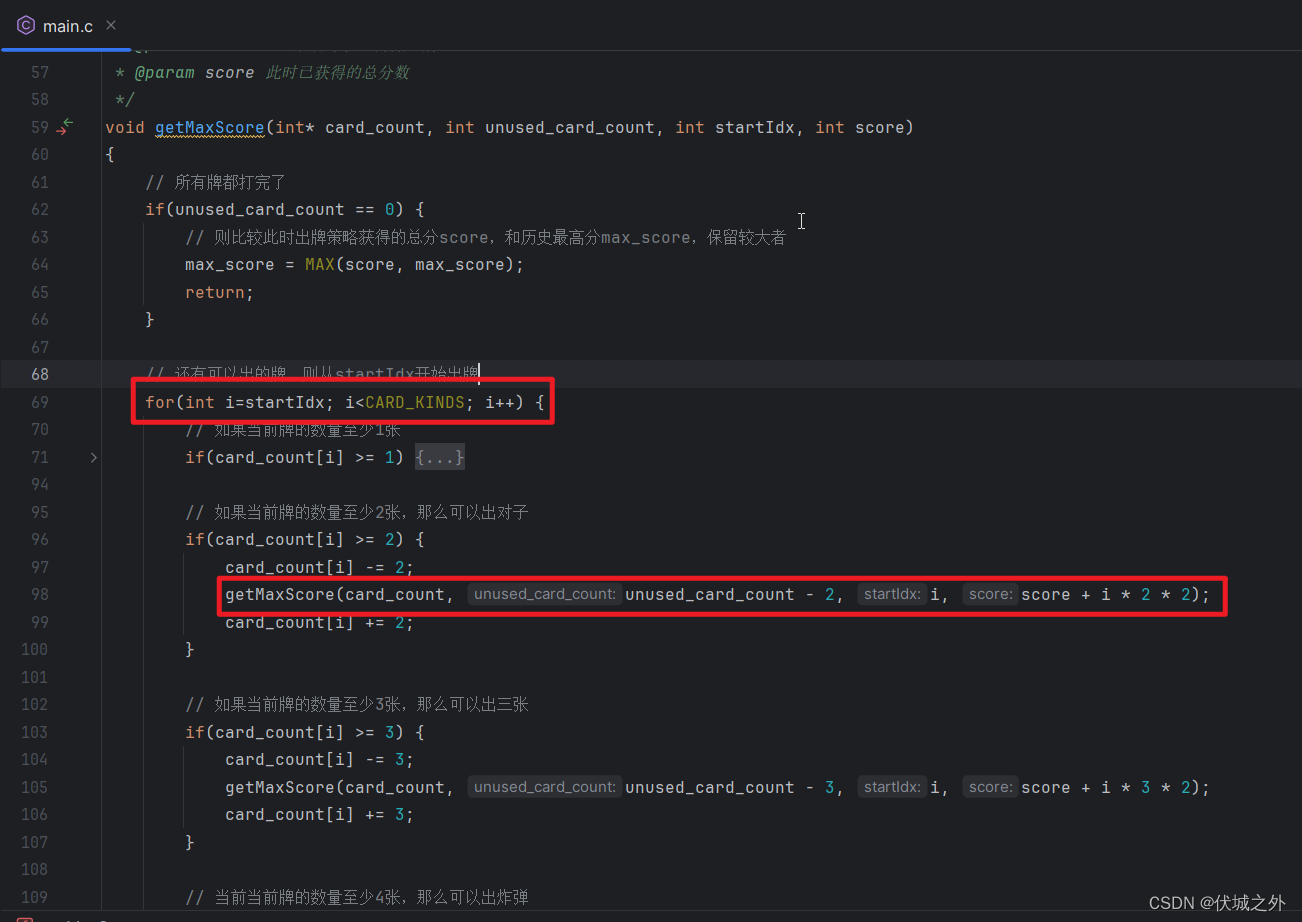
上面代码逻辑是存在重复探索的。
startIdx 位置的牌,可以从 for 循环进入出牌逻辑,也可以从 递归进入出牌逻辑,这会产生冗余探索。
我们可以只基于递归来完成所有出牌策略的探索。只是需要增加 card_count[startIdx] == 0 时,即 startIdx 位置没有牌时,自动递归到 startIdx + 1 位置出牌的逻辑。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const cards = await readline();
// 数组索引是牌面分数, 数组元素是牌面数量, 其中 0 索引不用
const card_count = new Array(14).fill(0);
// 统计各种牌的数量
for (let card of cards) {
// 1-9输入为数字1-9,10输入为数字0,JQK输入为大写字母JQK
// 1-9 牌面分数就是 1-9, 0的牌面分数是 10, J=11,Q=12,K=13, 可以发现牌面分数是连续的,可以和card_count数组的索引对应起来
if (card == "0") card_count[10]++;
else if (card == "J") card_count[11]++;
else if (card == "Q") card_count[12]++;
else if (card == "K") card_count[13]++;
else card_count[card - "0"]++;
}
// 记录最大得分
let max_score = 0;
getMaxScore(card_count, cards.length, 1, 0);
console.log(max_score);
/**
* 获取最大分数
* @param {*} card_count 各种牌的数量
* @param {*} unused_card_count 剩余牌的总数量
* @param {*} i 从哪个位置开始选牌
* @param {*} score 此时已获得的总分数
*/
function getMaxScore(card_count, unused_card_count, i, score) {
if (unused_card_count == 0) {
max_score = Math.max(max_score, score);
return;
}
// 没有可以出的牌,则继续递归到i+1开始出牌
if (card_count[i] == 0) {
getMaxScore(card_count, unused_card_count, i + 1, score);
}
// 还有可以出的牌,则从i开始出牌
// 如果当前牌的数量至少1张
if (card_count[i] >= 1) {
// 策略1、可以尝试出顺子,由于最大的顺子是9,10,J,Q,K,因此 i 作为顺子起始牌的话,不能超过9,且后续牌面 i+1, i+2, i+3, i+4 的数量都至少有1张
if (
i <= 9 &&
card_count[i + 1] >= 1 &&
card_count[i + 2] >= 1 &&
card_count[i + 3] >= 1 &&
card_count[i + 4] >= 1
) {
card_count[i] -= 1;
card_count[i + 1] -= 1;
card_count[i + 2] -= 1;
card_count[i + 3] -= 1;
card_count[i + 4] -= 1;
// 顺子是5张牌,因此出掉顺子后,可用牌数量减少5张,总分增加 (i + (i+1) + (i+2) + (i+3) + (i+4)) * 2
getMaxScore(
card_count,
unused_card_count - 5,
i,
score + (5 * i + 10) * 2
);
// 回溯
card_count[i] += 1;
card_count[i + 1] += 1;
card_count[i + 2] += 1;
card_count[i + 3] += 1;
card_count[i + 4] += 1;
}
// 策略2、出单张
card_count[i] -= 1;
getMaxScore(card_count, unused_card_count - 1, i, score + i);
card_count[i] += 1;
}
// 如果当前牌的数量至少2张,那么可以出对子
if (card_count[i] >= 2) {
card_count[i] -= 2;
getMaxScore(card_count, unused_card_count - 2, i, score + i * 2 * 2);
card_count[i] += 2;
}
// 如果当前牌的数量至少3张,那么可以出三张
if (card_count[i] >= 3) {
card_count[i] -= 3;
getMaxScore(card_count, unused_card_count - 3, i, score + i * 3 * 2);
card_count[i] += 3;
}
// 当前当前牌的数量至少4张,那么可以出炸弹
if (card_count[i] >= 4) {
card_count[i] -= 4;
getMaxScore(card_count, unused_card_count - 4, i, score + i * 4 * 3);
card_count[i] += 4;
}
}
})();
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(getResult(sc.nextLine()));
}
// 保存最大分数
static int max_score = 0;
public static int getResult(String cards) {
// 数组索引是牌面分数, 数组元素是牌面数量, 其中 0 索引不用
int[] card_count = new int[14];
// 统计各种牌的数量
for (int i = 0; i < cards.length(); i++) {
char card = cards.charAt(i);
// 1-9输入为数字1-9,10输入为数字0,JQK输入为大写字母JQK
// 1-9 牌面分数就是 1-9, 0的牌面分数是 10, J=11,Q=12,K=13, 可以发现牌面分数是连续的,可以和card_count数组的索引对应起来
if (card == '0') card_count[10]++;
else if (card == 'J') card_count[11]++;
else if (card == 'Q') card_count[12]++;
else if (card == 'K') card_count[13]++;
else card_count[card - '0']++;
}
getMaxScore(card_count, cards.length(), 1, 0);
return max_score;
}
/**
* 获取最大分数
*
* @param card_count 各种牌的数量
* @param unused_card_count 剩余牌的总数量
* @param startIdx 从哪个位置开始选牌
* @param score 此时已获得的总分数
*/
public static void getMaxScore(int[] card_count, int unused_card_count, int startIdx, int score) {
// 所有牌都打完了
if (unused_card_count == 0) {
// 则比较此时出牌策略获得的总分score,和历史最高分max_score,保留较大者
max_score = Math.max(score, max_score);
return;
}
// 没有可以出的牌,则继续递归到startIdx+1开始出牌
if (card_count[startIdx] == 0) {
getMaxScore(card_count, unused_card_count, startIdx + 1, score);
}
// 还有可以出的牌,则从startIdx开始出牌
// 如果当前牌的数量至少1张
if (card_count[startIdx] >= 1) {
// 策略1、可以尝试出顺子,由于最大的顺子是9,10,J,Q,K,因此 i 作为顺子起始牌的话,不能超过9,且后续牌面 i+1, i+2, i+3, i+4 的数量都至少有1张
if (startIdx <= 9
&& card_count[startIdx + 1] >= 1
&& card_count[startIdx + 2] >= 1
&& card_count[startIdx + 3] >= 1
&& card_count[startIdx + 4] >= 1) {
card_count[startIdx] -= 1;
card_count[startIdx + 1] -= 1;
card_count[startIdx + 2] -= 1;
card_count[startIdx + 3] -= 1;
card_count[startIdx + 4] -= 1;
// 顺子是5张牌,因此出掉顺子后,可用牌数量减少5张,总分增加 (i + (i+1) + (i+2) + (i+3) + (i+4)) * 2
getMaxScore(card_count, unused_card_count - 5, startIdx, score + (5 * startIdx + 10) * 2);
// 回溯
card_count[startIdx] += 1;
card_count[startIdx + 1] += 1;
card_count[startIdx + 2] += 1;
card_count[startIdx + 3] += 1;
card_count[startIdx + 4] += 1;
}
// 策略2、出单张
card_count[startIdx] -= 1;
getMaxScore(card_count, unused_card_count - 1, startIdx, score + startIdx);
card_count[startIdx] += 1;
}
// 如果当前牌的数量至少2张,那么可以出对子
if (card_count[startIdx] >= 2) {
card_count[startIdx] -= 2;
getMaxScore(card_count, unused_card_count - 2, startIdx, score + startIdx * 2 * 2);
card_count[startIdx] += 2;
}
// 如果当前牌的数量至少3张,那么可以出三张
if (card_count[startIdx] >= 3) {
card_count[startIdx] -= 3;
getMaxScore(card_count, unused_card_count - 3, startIdx, score + startIdx * 3 * 2);
card_count[startIdx] += 3;
}
// 当前当前牌的数量至少4张,那么可以出炸弹
if (card_count[startIdx] >= 4) {
card_count[startIdx] -= 4;
getMaxScore(card_count, unused_card_count - 4, startIdx, score + startIdx * 4 * 3);
card_count[startIdx] += 4;
}
}
}
Python算法源码
# 输入获取
cards = input()
# 保存最大分数
max_score = 0
# 获取牌的最大得分
def getMaxScore(card_count, unused_card_count, i, score):
"""
获取最大分数
:param card_count: 各种牌的数量
:param unused_card_count: 剩余牌的总数量
:param i: 从哪个位置开始选牌
:param score: 此时已获得的总分数
"""
global max_score
# 所有牌都打完了
if unused_card_count == 0:
# 则比较此时出牌策略获得的总分score,和历史最高分max_score,保留较大者
max_score = max(max_score, score)
return
# 没有可以出的牌,则继续递归到i+1开始出牌
if card_count[i] == 0:
getMaxScore(card_count, unused_card_count, i + 1, score);
# 还有可以出的牌,则从i开始出牌
# 如果当前牌的数量至少1张
if card_count[i] >= 1:
# 策略1、可以尝试出顺子,由于最大的顺子是9,10,J,Q,K,因此 i 作为顺子起始牌的话,不能超过9,且后续牌面 i+1, i+2, i+3, i+4 的数量都至少有1张
if i <= 9 and card_count[i + 1] >= 1 and card_count[i + 2] >= 1 and card_count[i + 3] >= 1 and card_count[i + 4] >= 1:
card_count[i] -= 1
card_count[i + 1] -= 1
card_count[i + 2] -= 1
card_count[i + 3] -= 1
card_count[i + 4] -= 1
# 顺子是5张牌,因此出掉顺子后,可用牌数量减少5张,总分增加 (i + (i+1) + (i+2) + (i+3) + (i+4)) * 2
getMaxScore(card_count, unused_card_count - 5, i, score + (5 * i + 10) * 2)
# 回溯
card_count[i] += 1
card_count[i + 1] += 1
card_count[i + 2] += 1
card_count[i + 3] += 1
card_count[i + 4] += 1
# 策略2、出单张
card_count[i] -= 1
getMaxScore(card_count, unused_card_count - 1, i, score + i)
card_count[i] += 1
# 如果当前牌的数量至少2张,那么可以出对子
if card_count[i] >= 2:
card_count[i] -= 2
getMaxScore(card_count, unused_card_count - 2, i, score + i * 2 * 2)
card_count[i] += 2
# 如果当前牌的数量至少3张,那么可以出三张
if card_count[i] >= 3:
card_count[i] -= 3
getMaxScore(card_count, unused_card_count - 3, i, score + i * 3 * 2)
card_count[i] += 3
# 当前当前牌的数量至少4张,那么可以出炸弹
if card_count[i] >= 4:
card_count[i] -= 4
getMaxScore(card_count, unused_card_count - 4, i, score + i * 4 * 3)
card_count[i] += 4
# 算法入口
def getResult():
# 数组索引是牌面分数, 数组元素是牌面数量, 其中 0 索引不用
card_count = [0] * 14
# 统计各种牌的数量
for card in cards:
# 1-9输入为数字1-9,10输入为数字0,JQK输入为大写字母JQK
# 1-9 牌面分数就是 1-9, 0的牌面分数是 10, J=11,Q=12,K=13, 可以发现牌面分数是连续的,可以和card_count数组的索引对应起来
if card == '0':
card_count[10] += 1
elif card == 'J':
card_count[11] += 1
elif card == 'Q':
card_count[12] += 1
elif card == 'K':
card_count[13] += 1
else:
i = ord(card) - ord('0')
card_count[i] += 1
getMaxScore(card_count, len(cards), 1, 0)
return max_score
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <string.h>
#define MAX_SIZE 15
#define CARD_KINDS 14
#define MAX(a, b) a > b ? a : b
void getMaxScore(int *card_count, int unused_card_count, int startIdx, int score);
int max_score = 0; // 保存最大分数
int main() {
char cards[MAX_SIZE];
scanf("%s", cards);
// 数组索引是牌面分数, 数组元素是牌面数量, 其中 0 索引不用
int card_count[CARD_KINDS] = {0};
// 统计各种牌的数量
for (int i = 0; i < strlen(cards); i++) {
char card = cards[i];
// 1-9输入为数字1-9,10输入为数字0,JQK输入为大写字母JQK
// 1-9 牌面分数就是 1-9, 0的牌面分数是 10, J=11,Q=12,K=13, 可以发现牌面分数是连续的,可以和card_count数组的索引对应起来
switch (card) {
case '0':
card_count[10]++;
break;
case 'J':
card_count[11]++;
break;
case 'Q':
card_count[12]++;
break;
case 'K':
card_count[13]++;
break;
default:
card_count[card - '0']++;
}
}
getMaxScore(card_count, strlen(cards), 1, 0);
printf("%dn", max_score);
return 0;
}
/**
* 获取最大分数
*
* @param card_count 各种牌的数量
* @param unused_card_count 剩余牌的总数量
* @param i 从哪个位置开始选牌
* @param score 此时已获得的总分数
*/
void getMaxScore(int *card_count, int unused_card_count, int i, int score) {
// 所有牌都打完了
if (unused_card_count == 0) {
// 则比较此时出牌策略获得的总分score,和历史最高分max_score,保留较大者
max_score = MAX(score, max_score);
return;
}
// 没有可以出的牌,则继续递归到i+1开始出牌
if(card_count[i] == 0) {
getMaxScore(card_count, unused_card_count, i + 1, score);
}
// 还有可以出的牌,则从i开始出牌
// 如果当前牌的数量至少1张
if (card_count[i] >= 1) {
// 策略1、可以尝试出顺子,由于最大的顺子是9,10,J,Q,K,因此 i 作为顺子起始牌的话,不能超过9,且后续牌面 i+1, i+2, i+3, i+4 的数量都至少有1张
if (i <= 9 && card_count[i + 1] >= 1 && card_count[i + 2] >= 1 && card_count[i + 3] >= 1 &&
card_count[i + 4] >= 1) {
card_count[i] -= 1;
card_count[i + 1] -= 1;
card_count[i + 2] -= 1;
card_count[i + 3] -= 1;
card_count[i + 4] -= 1;
// 顺子是5张牌,因此出掉顺子后,可用牌数量减少5张,总分增加 (i + (i+1) + (i+2) + (i+3) + (i+4)) * 2
getMaxScore(card_count, unused_card_count - 5, i, score + (5 * i + 10) * 2);
// 回溯
card_count[i] += 1;
card_count[i + 1] += 1;
card_count[i + 2] += 1;
card_count[i + 3] += 1;
card_count[i + 4] += 1;
}
// 策略2、出单张
card_count[i] -= 1;
getMaxScore(card_count, unused_card_count - 1, i, score + i);
card_count[i] += 1;
}
// 如果当前牌的数量至少2张,那么可以出对子
if (card_count[i] >= 2) {
card_count[i] -= 2;
getMaxScore(card_count, unused_card_count - 2, i, score + i * 2 * 2);
card_count[i] += 2;
}
// 如果当前牌的数量至少3张,那么可以出三张
if (card_count[i] >= 3) {
card_count[i] -= 3;
getMaxScore(card_count, unused_card_count - 3, i, score + i * 3 * 2);
card_count[i] += 3;
}
// 当前当前牌的数量至少4张,那么可以出炸弹
if (card_count[i] >= 4) {
card_count[i] -= 4;
getMaxScore(card_count, unused_card_count - 4, i, score + i * 4 * 3);
card_count[i] += 4;
}
}免责声明:
评论0