题目描述
给定一个由若干整数组成的数组nums,请检查数组是否是由某个子数组重复循环拼接而成,请输出这个最小的子数组。
输入描述
第一行输入数组中元素个数n,1 ≤ n ≤ 100000
第二行输入数组的数字序列nums,以空格分割,0 ≤ nums[i] < 10
输出描述
输出最小的子数组的数字序列,以空格分割;
备注
数组本身是其最大的子数组,循环1次可生成的自身;
用例
| 输入 | 9 1 2 1 1 2 1 1 2 1 |
| 输出 | 1 2 1 |
| 说明 | 数组[1,2,1,1,2,1,1,2,1] 可由子数组[1,2,1]重复循环3次拼接而成 |
题目解析
本题可以转化为最小重复子串问题,利用KMP算法求解。
比如,有一个字符串"abababab",该字符串可以看成是某个子串重复多次产生的,比如这个重复子串可以是"ab",也可以是"abab"。其中"ab"就是最小重复子串。
而求解最小重复子串问题,具有一定的技巧:
字符串S,长度为n,如果确定了S是由某子串重复产生的,则我们可以求解求解出字符串S的最长相同前后缀的长度m,则n-m就是最小重复子串的长度,而字符串S的0~n-m范围的子串就是其最小重复子串。
上面逻辑中,由一个“最长相同前后缀”的概念,首先大家需要知道字符串s的前缀、后缀的定义:
- 前缀,即起始索引必须为0,结束索引必须 < s.length – 1 的所有子串
- 后缀,即结束所有必须为s.length – 1,起始索引必须 > 0 的所有子串
- 前缀、后缀的长度 必须 < s.length,即前后缀不能是s本身,当然也不能为空
比如我们可以列出字符串"abababab"的所有前、后缀:
先画图看下几个例子:
长度为1的前缀(绿色部分)、后缀(橙色部分)
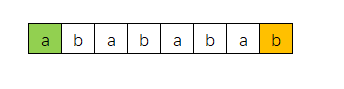
长度为2的前缀(绿色部分)、后缀(橙色部分)
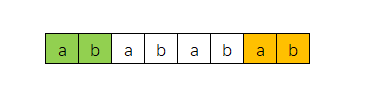
长度为3的前缀(绿色部分)、后缀(橙色部分)
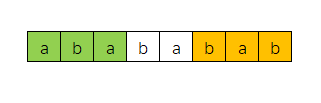
长度为6的前缀(绿色部分),后缀(橙色部分)
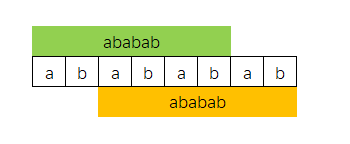
所有的前后缀情况如下表:
| 长度 | 前缀 | 后缀 |
| 1 | a | b |
| 2 | ab | ab |
| 3 | aba | bab |
| 4 | abab | abab |
| 5 | ababa | babab |
| 6 | ababab | ababab |
| 7 | abababa | bababab |
根据上面表,我们可以知道,
最长且相同的前、后缀是,长度为6的"ababab"
那么根据前面的技巧,
如果字符串s是由最小重复子串x重复产生的,则最小重复子串x的长度 = s.length – 最长相同前后缀.length
即字符串"abababab"的最小重复子串长度为2。
下面我们来推导下,为什么:最小重复子串的长度 = s.length – 最长相同前后缀.length
假设,字符串S的最小重复子串为x,且字符串S一共由k个最小重复子串x组成
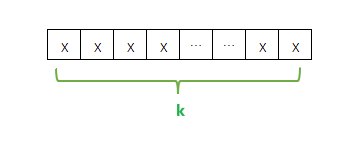
那么字符串S的最长相同前、后缀必然是(k-1)个x
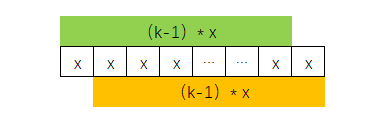
这里,大家推导一下,
假设上面:
前缀(绿色部分)再扩展一点,即侵入最后一个x串的左边部分,那么为了保持相同的前后缀,则后缀部分(橙色部分)必然需要再侵入第一个x的右边部分
那么有没有办法将x分为左L、右R两部分,使得下面等式成立呢?
( k – 1) * x + L == R + ( k – 1) * x;其中L + R == x
我们再简化下上面等式,即将(k-1) * x 替换为Y
Y + L == R + Y;其中L + R == x
其实上面等式的唯一成立条件就是:L = R
但是这是不可能的,因为x本身已经是最小重复子串了,因此本身不可能是由两个重复部分组成的。
现在,我们已经验证了:
如果字符串s是由最小重复子串x重复产生的,则最小重复子串x的长度 = s.length – 最长相同前后缀.length
那么,接下来,还有两个难点要解决:
1、如何求解字符串的最长相同前后缀的长度
关于最长相同前后缀的长度求解,我们可以基于KMP算法求解,具体请看:
中前缀表生成逻辑,以及getNext代码实现的逻辑。
2、如何证明一个字符串s是重复子串x生成的
假设字符串S是重复子串产生的,字符串S的长度为n,其最长相同前后缀长度为m,则 n – m 就是最小重复子串的长度,则这个最小重复字符串长度一定可以被字符串长度整除。
因此,我们只需要验证 n % (n – m) == 0 即可判断字符串S是否是重复的。
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length == 2) {
const n = parseInt(lines[0]);
const nums = lines[1].split(" ").map(Number);
console.log(getResult(n, nums));
lines.length = 0;
}
});
function getResult(n, nums) {
// KMP算法 前缀表求解
const next = getNext(n, nums);
// 最长相同前后缀长度
const m = next[n - 1];
// 最小重复子串的长度
const len = n % (n - m) == 0 ? n - m : n;
return nums.slice(0, len).join(" ");
}
function getNext(n, nums) {
const next = new Array(n).fill(0);
let j = 1;
let k = 0;
while (j < n) {
if (nums[j] == nums[k]) {
next[j] = k + 1;
j++;
k++;
} else {
if (k > 0) {
k = next[k - 1];
} else {
j++;
}
}
}
return next;
}
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
import java.util.StringJoiner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
int[] nums = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
System.out.println(getResult(n, nums));
}
public static String getResult(int n, int[] nums) {
// KMP算法 前缀表求解
int[] next = getNext(n, nums);
// 最长相同前后缀长度
int m = next[n - 1];
// 最小重复子串的长度
int len = n % (n - m) == 0 ? n - m : n;
StringJoiner sj = new StringJoiner(" ");
for (int i = 0; i < len; i++) sj.add(nums[i] + "");
return sj.toString();
}
public static int[] getNext(int n, int[] nums) {
int[] next = new int[n];
int j = 1;
int k = 0;
while (j < n) {
if (nums[j] == nums[k]) {
next[j] = k + 1;
j++;
k++;
} else {
if (k > 0) {
k = next[k - 1];
} else {
j++;
}
}
}
return next;
}
}
Python算法源码
# 输入获取
n = int(input())
nums = list(map(int, input().split()))
def getNext():
nxt = [0] * n
j = 1
k = 0
while j < n:
if nums[j] == nums[k]:
nxt[j] = k + 1
j += 1
k += 1
else:
if k > 0:
k = nxt[k - 1]
else:
j += 1
return nxt
# 算法入口
def getResult():
# KMP算法 前缀表求解
nxt = getNext()
# 最长相同前后缀长度
m = nxt[n-1]
# 最小重复子串的长度
length = n - m if n % (n - m) == 0 else n
return " ".join(map(str, nums[0:length]))
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <string.h>
#define MAX_SIZE 100000
char* getResult(int n, int* nums);
int* getNext(int n, int* nums);
void join(int* arr, int arr_size, char delimiter[], char tmp_str[], char result_str[]);
int nums[MAX_SIZE];
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &nums[i]);
}
printf(getResult(n, nums));
return 0;
}
char result_str[MAX_SIZE * 3];
char* getResult(int n, int* nums)
{
// KMP算法 前缀表求解
int* next = getNext(n, nums);
// 最长相同前后缀长度
int m = next[n - 1];
// 最小重复子串的长度
int len = n % (n - m) == 0 ? n - m : n;
char tmp_str[2];
join(nums, len, " ", tmp_str, result_str);
return result_str;
}
// KMP算法 前缀表求解
int next[MAX_SIZE] = { 0 };
int* getNext(int n, int* nums)
{
int j = 1;
int k = 0;
while (j < n) {
if (nums[j] == nums[k]) {
next[j] = k + 1;
j++;
k++;
}
else {
if (k > 0) {
k = next[k - 1];
}
else {
j++;
}
}
}
return next;
}
// 整型数组arr按照指定连接符delimiter进行拼接得到字符串result_str
void join(int* arr, int arr_size, char delimiter[], char tmp_str[], char result_str[])
{
for (int i = 0; i < arr_size; i++) {
sprintf(tmp_str, "%d", arr[i]);
strcat(result_str, tmp_str);
if (i != arr_size - 1) {
strcat(result_str, delimiter);
}
}
}免责声明:
评论0