题目描述
某通信网络中有N个网络结点,用1到N进行标识。
网络中的结点互联互通,且结点之间的消息传递有时延,相连结点的时延均为一个时间单位。
现给定网络结点的连接关系link[i]={u,v},其中u和v表示网络结点。
当指定一个结点向其他结点进行广播,所有被广播结点收到消息后都会在原路径上回复一条响应消息,请计算发送结点至少需要等待几个时间单位才能收到所有被广播结点的响应消息。
注:
- N的取值范围为[1,100];
- 连接关系link的长度不超过3000,且1 <= u,v <= N;
- 网络中任意结点间均是可达的;
输入描述
输入的第一行为两个正整数,分别表示网络结点的个数N,以及时延列表的长度T;
接下来的T行输入,表示结点间的连接关系列表;
最后一行的输入为一个正整数,表示指定的广播结点序号;
输出描述
输出一个整数,表示发送结点接收到所有响应消息至少需要等待的时长。
用例
| 输入 | 5 7 1 4 2 1 2 3 2 4 3 4 3 5 4 5 2 |
| 输出 | 4 |
| 说明 | 结点2到5的最小时延为2,到剩余结点的最小时延均为1,所以至少要等待2*2=4s。 |
题目解析
题目用例的连接图如下
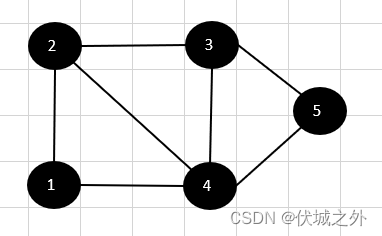
本题其实就是求解单源最短路径,可以使用dijkstra算法。
关于dijkstra算法可以参考
2023.06.06
本题是无向图,即点与点之间都是双向连接,因此构建邻接表时,需要注意双向性。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, t;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
[n, t] = lines[0].split(" ").map(Number);
}
if (t && lines.length === t + 2) {
lines.shift();
const src = parseInt(lines.pop());
const relations = lines.map((line) => line.split(" ").map(Number));
console.log(getMaxRespTime(n, src, relations));
lines.length = 0;
}
});
function getMaxRespTime(n, k, relations) {
// 邻接表
const graph = {};
// 初始化邻接表
for (let i = 0; i < relations.length; i++) {
const [p1, p2] = relations[i];
graph[p1] ? graph[p1].push(p2) : (graph[p1] = [p2]);
graph[p2] ? graph[p2].push(p1) : (graph[p2] = [p1]);
}
// dist用于统计源点到图中各点的最短距离,初始化最短距离为Infinity,由于题目要求网络节点从1开始,因此这里数组长度设为n+1
const dist = new Array(n + 1).fill(Infinity);
// 源点到自身的最短距离是0
dist[k] = 0;
// needCheck是一个优先队列,用于存储每轮路径查找中确认了最短路径的目标点v
const needCheck = [];
while (true) {
let flag = false;
// graph[k]是一个数组,存储的是源点k的下一步相邻节点v
graph[k]?.forEach((v) => {
let newDist = dist[k] + 1; // 题目说相邻节点的传输时延是1
// 如果本次路径下,源点k到目标点v的距离小于上次统计的,则更新
if (dist[v] > newDist) {
dist[v] = newDist;
// 如果优先队列中没有目标点v,则加入
if (needCheck.indexOf(v) === -1) {
needCheck.push(v);
flag = true;
}
}
});
// 如果优先队列为空,则结束循环
if (!needCheck.length) break;
// 如果优先队列有新节点加入,则重新排序,到源点k距离最小的点v,当成下次循环的新源点
if (flag) needCheck.sort((a, b) => dist[a] - dist[b]);
// 取出队头,当成新源点,进入下次循环
k = needCheck.shift();
}
// dist初始化为n+1长度的数组,头部不对应任何节点,节点只取索引1~n,因此头部弹出
dist.shift();
// 由于题目说所有网络节点均互联,因此不存在零散点,即所有节点到源点距离均不可能是Infinity,因此可以直接取最大的
let ans = Math.max(...dist);
// 本题要求最长响应时间,即往返时间
return ans * 2;
}
上面算法中,优先队列是基于有序数组实现的,但是优先队列其实并不需要维护成整体有序,只需要保证队头元素总是优先级最高的即可。
因此,我们可以基于堆结构(完全二叉树)来实现优先队列,关于优先队列的原理和实现,请看
LeetCode – 1705 吃苹果的最大数目_伏城之外的博客-CSDN博客
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, t;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
[n, t] = lines[0].split(" ").map(Number);
}
if (t && lines.length === t + 2) {
lines.shift();
const src = parseInt(lines.pop());
const relations = lines.map((line) => line.split(" ").map(Number));
console.log(getMaxRespTime(n, src, relations));
lines.length = 0;
}
});
function getMaxRespTime(n, k, relations) {
const graph = {};
for (let [u, v] of relations) {
graph[u] ? graph[u].push(v) : (graph[u] = [v]);
graph[v] ? graph[v].push(u) : (graph[v] = [u]);
}
const dist = new Array(n + 1).fill(Infinity);
dist[k] = 0;
const pq = new MyPriorityQueue((a, b) => a[1] - b[1]);
while (true) {
graph[k]?.forEach((v) => {
const newDist = dist[k] + 1;
if (newDist < dist[v]) {
dist[v] = newDist;
pq.push([v, dist[v]]);
}
});
if (pq.isEmpty()) break;
k = pq.shift()[0];
}
dist.shift();
const ans = Math.max(...dist);
return ans * 2;
}
class MyPriorityQueue {
constructor(compare) {
this.queue = [];
this.compare = compare;
}
#swap(i, j) {
const tmp = this.queue[i];
this.queue[i] = this.queue[j];
this.queue[j] = tmp;
}
#sink() {
let k = 0;
while (true) {
let l = 2 * k + 1;
let r = l + 1;
let fa = this.queue[k];
let leftCh = this.queue[l];
let rightCh = this.queue[r];
let targetCh;
let t;
if (leftCh && rightCh) {
if (this.compare(leftCh, rightCh) < 0) {
targetCh = leftCh;
t = l;
} else {
targetCh = rightCh;
t = r;
}
} else if (!leftCh && rightCh) {
targetCh = rightCh;
t = r;
} else if (!rightCh && leftCh) {
targetCh = leftCh;
t = l;
} else {
break;
}
if (this.compare(targetCh, fa) < 0) {
this.#swap(t, k);
k = t;
} else {
break;
}
}
}
#swim() {
let c = this.queue.length - 1;
while (c !== 0) {
let f = Math.floor((c - 1) / 2);
let fa = this.queue[f];
let ch = this.queue[c];
if (this.compare(fa, ch) > 0) {
this.#swap(c, f);
c = f;
} else {
break;
}
}
}
isEmpty() {
return this.queue.length === 0;
}
top() {
return this.queue[0];
}
shift() {
this.#swap(this.queue.length - 1, 0);
const res = this.queue.pop();
this.#sink();
return res;
}
push(ele) {
this.queue.push(ele);
this.#swim();
}
}
Java算法源码
import java.util.ArrayList;
import java.util.HashMap;
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int t = sc.nextInt();
int[][] relations = new int[t][2];
for (int i = 0; i < t; i++) {
relations[i][0] = sc.nextInt();
relations[i][1] = sc.nextInt();
}
int src = sc.nextInt();
System.out.println(getResult(n, src, relations));
}
public static int getResult(int n, int src, int[][] relations) {
HashMap<Integer, ArrayList<Integer>> graph = new HashMap<>();
for (int[] relation : relations) {
int u = relation[0];
int v = relation[1];
graph.putIfAbsent(u, new ArrayList<>());
graph.get(u).add(v);
graph.putIfAbsent(v, new ArrayList<>());
graph.get(v).add(u);
}
ArrayList<Integer> dist = new ArrayList<>();
for (int i = 0; i < n + 1; i++) {
dist.add(Integer.MAX_VALUE);
}
dist.set(src, 0);
PriorityQueue<Integer[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);
while (true) {
if (graph.containsKey(src)) {
for (Integer v : graph.get(src)) {
int newDist = dist.get(src) + 1;
if (newDist < dist.get(v)) {
dist.set(v, newDist);
pq.offer(new Integer[] {v, newDist});
}
}
}
if (pq.isEmpty()) break;
src = pq.poll()[0];
}
dist.remove(0);
return dist.stream().max((a, b) -> a - b).get() * 2;
}
}
Python算法源码
# 输入获取
import queue
import sys
n, t = map(int, input().split())
relations = [list(map(int, input().split())) for _ in range(t)]
src = int(input())
# 算法入口
def getResult(n, src, relations):
graph = {}
for u, v in relations:
if graph.get(u) is None:
graph[u] = []
graph[u].append(v)
if graph.get(v) is None:
graph[v] = []
graph[v].append(u)
dist = [sys.maxsize] * (n + 1)
dist[src] = 0
pq = queue.PriorityQueue()
while True:
if graph.get(src) is not None:
for v in graph[src]:
newDist = dist[src] + 1
if newDist < dist[v]:
dist[v] = newDist
pq.put([newDist, v])
if pq.qsize() == 0:
break
src = pq.get()[1]
dist.pop(0)
return max(dist) * 2
# 算法调用
print(getResult(n, src, relations))
免责声明:
1、IT资源小站为非营利性网站,全站所有资料仅供网友个人学习使用,禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享,本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题,请立即告知本站,本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体,但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员,一律视为同意网站规定,本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0