题目描述
在一个博客网站上,每篇博客都有评论。
每一条评论都是一个非空英文字母字符串。
评论具有树状结构,除了根评论外,每个评论都有一个父评论。
当评论保存时,使用以下格式:
- 首先是评论的内容;
- 然后是回复当前评论的数量。
- 最后是当前评论的所有了评论。(子评论使用相同的格式嵌套存储)
所有元素之间都用单个逗号分隔。
例如,如果评论如下:

第一条评论是"helo,2,ok,0,bye,0",第二条评论是"test,0",第三条评论是"one,1,two,1,a,0"。
所有评论被保存成"hello,2,ok,0.bye,0,test,0,one,1,two,1,a,0"。
对于上述格式的评论,请以另外一种格式打印:
- 首先打印评论嵌套的最大深度。
- 然后是打印n行,第 i (1 ≤ i ≤ n) 行对应于嵌套级别为 i 的评论 (根评论的嵌套级别为1)。
- 对于第 i 行,嵌套级别为的评论按照它们出现的顺序打印,用空格分隔开。
输入描述
一行评论。由英文字母、数字和英文逗号组成。
保证每个评论都是由英文字符组成的非空字符串。
每个评论的数量都是整数 (至少由一个数字组成)。
整个字符串的长度不超过10^6。
给定的评论结构保证是合法的。
输出描述
按照给定的格式打印评论。对于每一级嵌套,评论应该按照输入中的顺序打印。
用例
| 输入 | hello,2,ok,0,bye,0,test,0,one,1,two,1,a,0 |
| 输出 | 3 hello test one ok bye two a |
| 说明 | 如题目描述中图所示,最大嵌套级别为3,嵌套级别为1的评论是"hello test one",嵌套级别为2的评论是"ok bye two",嵌套级别为3的评论为”a"”。 |
| 输入 | A,5,A,0,a,0,A,0,a,0,A,0 |
| 输出 | 2 A A a A a A |
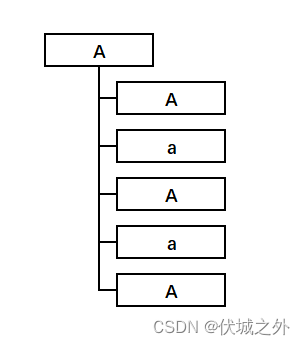
| 说明 |
如下图所示,最大嵌套级别为2,嵌套级别为1的评论是"A”,嵌套级别为2的评论是"A a A a A"
|
| 输入 | A,3,B,2,C,0,D,1,E,0,F,1,G,0,H,1,I,1,J,0,K,1,L,0,M,2,N,0,O,1,P,0 |
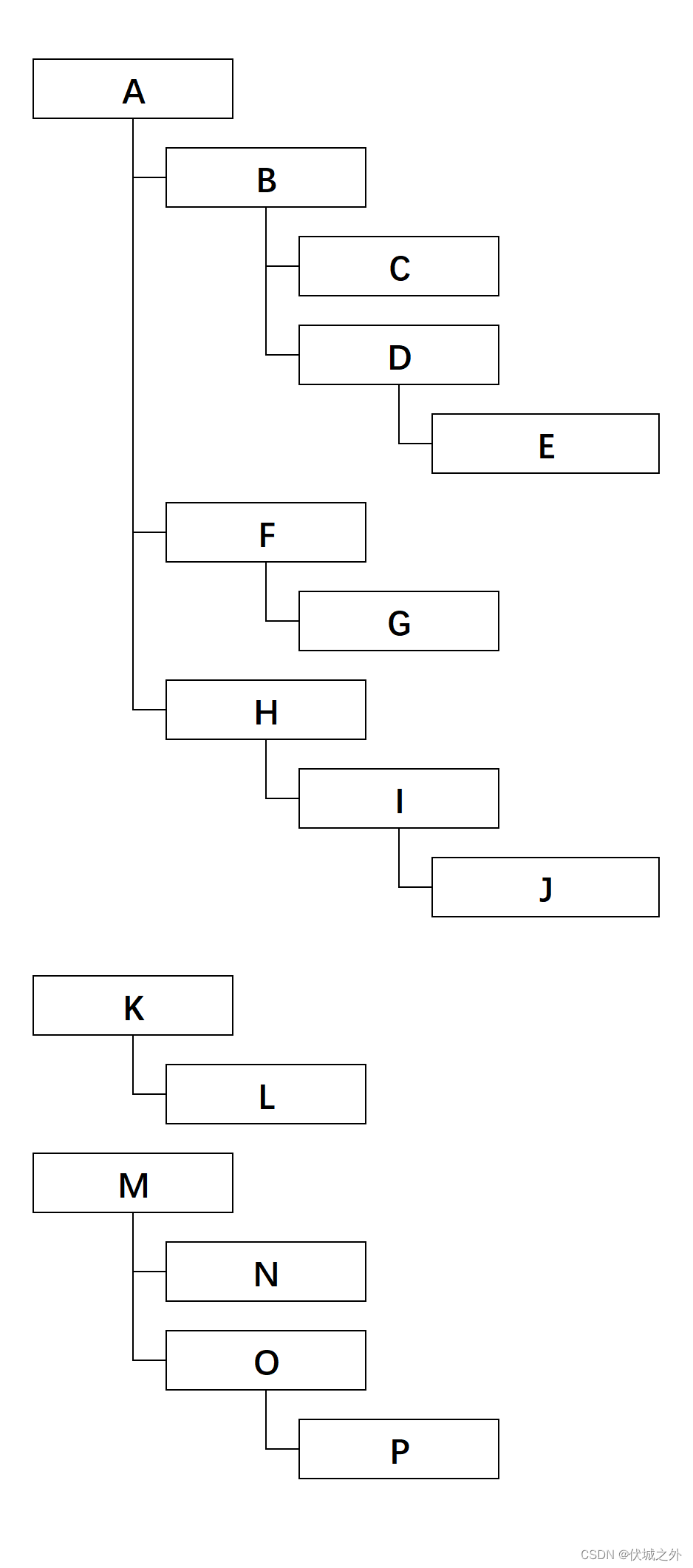
| 输出 | 4 A K M B F H L N O C D G I P E J |
| 说明 |
如下图所示
|
题目解析
本题的评论嵌套其实就是一个树形结构。比如用例1:
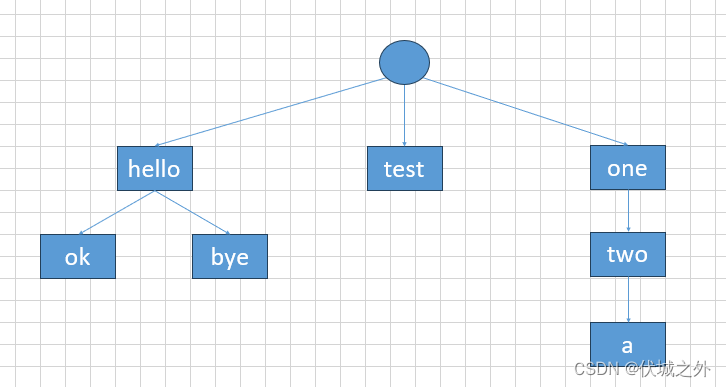
最终题目要求的:
- 评论嵌套的最大深度 → 其实就是树的高度
- 嵌套级别为 i 的评论 → 其实就是树的第 i 层的所有节点
因此,本题我们需要还原出一个树结构。
那么,我们如何从一个字符串数组,例如用例1:
hello,2,ok,0,bye,0,test,0,one,1,two,1,a,0
中,还原出一颗树呢?
字符串的组成是多个评论,每一个评论包括两个部分:评论内容 + 子评论数,比如用例1可以划分如下
【hello,2】,【ok,0】,【bye,0】,【test,0】,【one,1】,【two,1】,【a,0】
另外,每一个子评论都是紧跟着其父评论后面。如下面例子:
根评论A,子评论A1,子评论A2,根评论B,子评论B1,子评论B2
但是子评论本身也可以有子评论,因此完整的结构图应该是:
根评论A,子评论A1,子子评论A11,子子评论A12,子评论A2,子子评论A21,子子评论A22,根评论B,子评论B1,子子评论B11,子子评论B12, 子评论B2,子子评论B21,子子评论B22
这个时候,如果根据父评论的“子评论数”往后顺序遍历的话,得到的并不是该父评论的实际子评论信息。
正确的做法应该是递归的去遍历父评论的子评论。
比如,根评论A有2个子评论,分别是子评论A1,子评论A2,
因此,我们需要从根评论A开始往后遍历2个评论,但是每遍历一个评论,我们都需要检查被遍历的评论也有子评论,比如首先遍历到子评论A1,发现它也有2个子评论,分别是子子评论A11,子子评论A12,因此我们应该暂停根评论A的子评论遍历过程,而是优先去遍历其子评论A1的子子评论。
当然,如果子子评论也有子子子评论,则也需要按上面逻辑处理。
由于评论嵌套的层级是不确定的,因此上面过程需要使用递归。
在上面递归过程中,一个比较麻烦的问题是,递归处理完子评论A1后,如何反馈下一个子评论A2的位置给 → 重启遍历流程的根评论A。
因此,我们暂停根评论A的遍历流程时,对应的遍历指针指向的还是子评论A1的位置,而子评论A1递归结束后,重启遍历流程的根评论A的遍历流程指针还是指向子评论A1呢!!
这里为了避免繁琐的索引位置处理,我直接在一开始时,将所有的评论信息加入都队列中,每次都取出队头评论进行处理,这样的话,当前递归处理完子评论A1,那么队列头部自然而然就是子评论A2了。
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const comments = line.split(",");
getResult(comments);
});
function getResult(queue) {
// 树结构
const tree = [];
// 根评论层级为1
const level = 1;
// 该循环用于取出根评论
while (queue.length > 0) {
// 根评论
const comment = queue.shift();
// 如果树还没有对应层级,则初始化对应层级
if (tree.length < level) {
tree.push([]);
}
// 将根评论加入树结构的第一层
tree[0].push(comment);
// 该根评论有几个直接子评论
const childCount = parseInt(queue.shift());
// 按上面逻辑,递归处理子评论,子评论所处级别为level+1
recursive(queue, level + 1, childCount, tree);
}
// 树结构的高度,就是评论嵌套的最大深度
console.log(tree.length);
// 树结构的每一层,记录对应嵌套级别的评论
for (let levelNodes of tree) {
console.log(levelNodes.join(" "));
}
}
function recursive(queue, level, childCount, tree) {
for (let i = 0; i < childCount; i++) {
const comment = queue.shift();
if (tree.length < level) {
tree.push([]);
}
tree[level - 1].push(comment);
const count = parseInt(queue.shift());
if (count > 0) {
recursive(queue, level + 1, count, tree);
}
}
}
Java算法源码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String[] comments = sc.nextLine().split(",");
getResult(comments);
}
public static void getResult(String[] comments) {
// 树结构
ArrayList<ArrayList<String>> tree = new ArrayList<>();
// 将输入的评论信息,转化为队列结构
LinkedList<String> queue = new LinkedList<>(Arrays.asList(comments));
// 根评论层级为1
int level = 1;
// 该循环用于取出根评论
while (queue.size() > 0) {
// 根评论
String comment = queue.removeFirst();
// 如果树还没有对应层级,则初始化对应层级
if (tree.size() < level) {
tree.add(new ArrayList<>());
}
// 将根评论加入树结构的第一层
tree.get(0).add(comment);
// 该根评论有几个直接子评论
int childCount = Integer.parseInt(queue.removeFirst());
// 按上面逻辑,递归处理子评论,子评论所处级别为level+1
recursive(queue, level + 1, childCount, tree);
}
// 树结构的高度,就是评论嵌套的最大深度
System.out.println(tree.size());
// 树结构的每一层,记录对应嵌套级别的评论
for (ArrayList<String> levelNodes : tree) {
System.out.println(String.join(" ", levelNodes));
}
}
public static void recursive(
LinkedList<String> queue, int level, int childCount, ArrayList<ArrayList<String>> tree) {
for (int i = 0; i < childCount; i++) {
String comment = queue.removeFirst();
if (tree.size() < level) {
tree.add(new ArrayList<>());
}
tree.get(level - 1).add(comment);
int count = Integer.parseInt(queue.removeFirst());
if (count > 0) {
recursive(queue, level + 1, count, tree);
}
}
}
}
Python算法源码
import sys
# 本题可能Python会maximum recursion depth exceeded in comparison, 因此这里可以将递归深度搞大点
sys.setrecursionlimit(5000)
# 输入获取
queue = input().split(",")
def recursive(queue, level, childCount, tree):
for i in range(childCount):
comment = queue.pop(0)
if len(tree) < level:
tree.append([])
tree[level - 1].append(comment)
count = int(queue.pop(0))
if count > 0:
recursive(queue, level + 1, count, tree)
# 算法入口
def getResult(queue):
# 树结构
tree = []
# 根评论层级为1
level = 1
while len(queue) > 0:
# 根评论
comment = queue.pop(0)
# 如果树还没有对应层级,则初始化对应层级
if len(tree) < level:
tree.append([])
# 将根评论加入树结构的第一层
tree[0].append(comment)
# 该根评论有几个直接子评论
childCount = int(queue.pop(0))
# 按上面逻辑,递归处理子评论,子评论所处级别为level+1
recursive(queue, level + 1, childCount, tree)
# 树结构的高度,就是评论嵌套的最大深度
print(len(tree))
# 树结构的每一层,记录对应嵌套级别的评论
for levelNodes in tree:
print(" ".join(levelNodes))
# 算法调用
getResult(queue)免责声明:
评论0