题目描述
在做物理实验时，为了计算物体移动的速率，通过相机等工具周期性的采样物体移动距离。
由于工具故障，采样数据存在误差甚至错误的情况。
需要通过一个算法过滤掉不正确的采样值。
不同工具的故障模式存在差异，算法的各类门限会根据工具类型做相应的调整。
请实现一个算法，计算出给定一组采样值中正常值的最长连续周期。
判断第 i 个周期的采样数据 S[i] 是否正确的规则如下（假定物体移动速率不超过10个单元，前一个采样周期 S[i-1] )：
- S[i] <= 0，即为错误值
- S[i] < S[i-1]，即为错误值
- S[i] – S[i-1] >= 10，即为错误值
- 其它情况为正常值
判断工具是否故障的规则如下：
- 在M个周期内，采样数据为错误值的次数为T（次数可以不连续），则工具故障。
判断故障恢复的条件如下：
- 产生故障后的P个周期内，采样数据一直为正常值，则故障恢复。
错误采样数据的处理方式：
- 检测到故障后，丢弃从故障开始到故障恢复的采样数据。
- 在检测到工具故障之前，错误的采样数据，则由最近一个正常值代替；如果前面没有正常的采样值，则丢弃此采样数据。
给定一段周期的采样数据列表S，计算正常值的最长连续周期。
输入描述
故障确认周期数和故障次数门限分别为M和T，故障恢复周期数为P。
第 i 个周期，检测点的状态为Si
输入为两行，格式如下：
M T P
S1 S2 S3 …
M、T和P的取值范围为[1, 100000]
Si取值范围为[0, 100000]，i 从0开始编号
输出描述
一行输出正常值的最长连续周期
用例
| 输入 | 10 6 3 -1 1 2 3 100 10 13 9 10 |
| 输出 | 8 |
| 说明 | S[0]，S[4]，S[7]，S[8]为错误值。S[0]之前没有正常的采样数据，丢弃S[0]。S[4]和S[7]不满足故障条件，此值分别由S[3]和S[6]代替，即S[4]为3，S[7]为13。替换后，S[8]小于S[7]，也是错误值。 |
| 输入 | 5 3 3 0 1 2 -1 4 3 6 7 6 6 10 11 12 |
| 输出 | 9 |
| 说明 | S[3]，S[5]，S[8]，S[9]为错误值。从S[3]到S[7]的5个周期内只有两个错误值S[3]和S[5]。从S[5]到S[9]的5个周期内有三个错误值S[5]、S[8]和S[9]，工具故障。丢弃S[9]到S[12]的值。 |
| 输入 | 5 3 3 1 2 -1 -2 -3 6 7 8 9 10 11 12 |
| 输出 | 5 |
| 说明 | S[2]，S[3]，S[4]为错误值。从S[2]到S[6]的5个周期内有三个错误值，工具故障。丢弃S[4]到S[6]的值。有两段正常连续周期，S[0]到S[3]（周期数为4）和S[7]到S[11]（周期数为5）。 |
题目解析
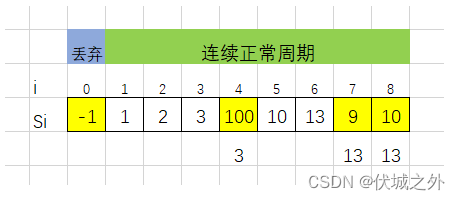
用例1图示（图示按照用例说明设计）
M = 10，T = 6，P = 3
S[0]，S[4]，S[7]，S[8]为错误值。
S[0]之前没有正常的采样数据，丢弃S[0]。
S[4]和S[7]不满足故障条件，此值分别由S[3]和S[6]代替，即S[4]为3，S[7]为13。
替换后，S[8]小于S[7]，也是错误值。
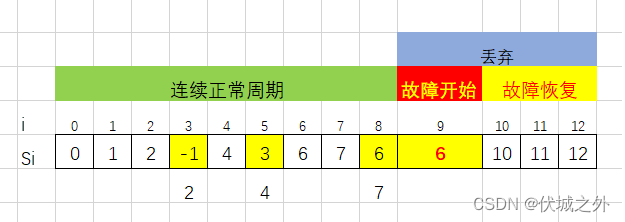
用例2图示（图示按照用例说明设计）
M = 5，T = 3，P = 3
S[3]，S[5]，S[8]，S[9]为错误值。
从S[3]到S[7]的5个周期内只有两个错误值S[3]和S[5]。
从S[5]到S[9]的5个周期内有三个错误值S[5]、S[8]和S[9]，工具故障。丢弃S[9]到S[12]的值。
个人疑惑：
s[0] ≤ 0，我理解应该记作错误值吧？因为题目说：S[i] <= 0，即为错误值。
按照题目意思，s[0]前面没有其他值，因此s[0]应该被丢弃，那么该用例的最长连续周期应该是1~8，长度为8。
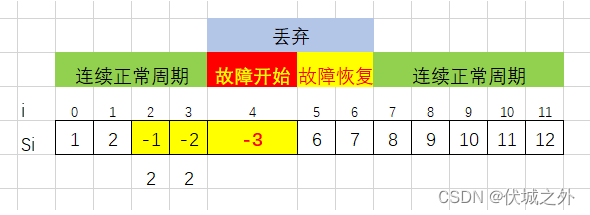
用例3图示（图示按照用例说明设计）
M = 5，T = 3，P = 3
S[2]，S[3]，S[4]为错误值。
从S[2]到S[6]的5个周期内有三个错误值，工具故障。丢弃S[4]到S[6]的值。有两段正常连续周期，S[0]到S[3]（周期数为4）和S[7]到S[11]（周期数为5）。
个人疑惑：
s[4]是故障开始点，而当前用例P=3，那么s[5]~s[7]应该是故障恢复检查时期，
按照题目意思：检测到故障后，丢弃从故障开始到故障恢复的采样数据。
那应该丢弃的是s[4]~s[7]吧？但是用例说明是：丢弃S[4]到S[6]的值。为什么s[7]不丢弃呢？
如果按照题目意思，应该要丢弃S[4]到S[7]，因此该用例的最长连续周期应该是4。
经过上面分析，这题的用例说明和题目描述简直就是自相矛盾……
我这里按照题目描述来实现。具体逻辑请看代码注释（主要是文字描述太复杂了）
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
// 故障确认周期数m, 故障次数门限t, 故障恢复周期数p
const [m, t, p] = (await readline()).split(" ").map(Number);
// 一段周期的采样数据列表
const s = (await readline()).split(" ").map(Number);
const NORMAL = 1; // 正常数据的状态
const FAULT = 2; // 错误数据的状态
const ABORT = 3; // 丢弃的状态
const RECOVERY_NORMAL = 4; // 故障恢复检查期间的正常数据的状态
const RECOVERY_FAULT = 5; // 故障恢复检查期间的错误数据的状态
// 记录每个采样数据的状态
const status = new Array(s.length).fill(0);
console.log(getResult());
function getResult() {
// M个周期可以当成滑窗，l是滑窗的左边界
let l = 0;
// 滑窗内错误数据的个数
let window_fault_count = 0;
// 滑窗右边界纳入新数据
for (let r = 0; r < s.length; r++) {
// 如果滑窗长度超过了m，那么滑窗的左边界需要右移
if (r - l + 1 > m) {
// 如果右移前的，滑窗左边界对于的数据状态是FAULT，则右移后的滑窗内错误数据个数-1
if (status[l++] == FAULT) window_fault_count--;
}
// 检查数据状态
if (check_normal(r)) {
// 如果数据正常，则标记status[r]为正常状态
status[r] = NORMAL;
} else {
// 如果数据异常，则需要检查当前数据前面一个数据的状态
if (r < 1 || status[r - 1] == ABORT) {
// 如果当前数据前面一个数据的状态是丢弃的，则当前数据没有代替值，也需要被丢弃
status[r] = ABORT;
// 一旦出现丢弃数据，则滑窗中断，此时需要重置滑窗
window_fault_count = 0;
l = r + 1;
} else {
// 如果当前数据前面一个数据的状态不是丢弃状态，那么滑窗内错误数据个数+1
if (++window_fault_count < t) {
// 如果滑窗内错误数据个数没有超过阈值t，那么可以用前面一个数据代替
status[r] = FAULT;
s[r] = s[r - 1];
} else {
// 如果滑窗内错误数据个数超过了阈值t，那么 r 位置就是故障开始的位置
// 此时 r 位置数据需要被丢弃，此时滑窗中断，需要重置滑窗
status[r] = ABORT;
window_fault_count = 0;
// i 位置就是 故障恢复检查期开始位置
let i = r + 1;
// 故障恢复检查期内连续正确数据个数
let recovery_correct_count = 0;
while (i < s.length) {
if (check_recovery(i)) {
recovery_correct_count++;
status[i] = RECOVERY_NORMAL;
// 当故障恢复期间，连续正确数据个数达到p，则故障解除
if (recovery_correct_count == p) break;
} else {
recovery_correct_count = 0;
status[i] = RECOVERY_FAULT;
}
i++;
}
// i 位置是故障解除的位置，则下一次，我们应该从 i+1 位置开始重新判断，即滑窗的左、右边界都要更新为i+1
if (i < s.length) {
l = i + 1;
r = i; // 这里r没有等于 i+1，是因为for循环会给r++
}
}
}
}
}
// 最后只需要找到 status 数组中最长的连续NORMAL和FAULT即可
let maxLen = 0;
let len = 0;
for (let sta of status) {
if (sta == NORMAL || sta == FAULT) {
len++;
} else {
maxLen = Math.max(maxLen, len);
len = 0;
}
}
return Math.max(maxLen, len);
}
// 正常期间检查
function check_normal(i) {
if (s[i] <= 0) return false; //S[i] <= 0，即为错误值
// 和前面采样数据比较的前提条件是：前面的采样数据必须是正常状态，或者正常期错误状态
if (i >= 1 && (status[i - 1] == NORMAL || status[i - 1] == FAULT)) {
if (s[i] < s[i - 1]) return false; // S[i] < S[i-1]，即为错误值
if (s[i] - s[i - 1] >= 10) return false; // S[i] - S[i-1] >= 10，即为错误值
}
return true; // 其它情况为正常值
}
// 故障恢复期检查
function check_recovery(i) {
if (s[i] <= 0) return false; // S[i] <= 0，即为错误值
// 和前面采样数据比较的前提条件是：前面的采样数据不能时丢弃状态，以及恢复期错误状态
if (i >= 1 && status != ABORT && status != RECOVERY_FAULT) {
if (s[i] < s[i - 1]) return false; // S[i] < S[i-1]，即为错误值
if (s[i] - s[i - 1] >= 10) return false; // S[i] - S[i-1] >= 10，即为错误值
}
return true; // 其它情况为正常值
}
})();
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
// 故障确认周期数m, 故障次数门限t, 故障恢复周期数p
static int m, t, p;
// 一段周期的采样数据列表
static int[] s;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] tmp = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
m = tmp[0];
t = tmp[1];
p = tmp[2];
s = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
System.out.println(getResult());
}
static int[] status;
static final int NORMAL = 1; // 正常数据的状态
static final int FAULT = 2; // 错误数据的状态
static final int ABORT = 3; // 丢弃的状态
static final int RECOVERY_NORMAL = 4; // 故障恢复检查期间的正常数据的状态
static final int RECOVERY_FAULT = 5; // 故障恢复检查期间的错误数据的状态
public static int getResult() {
// 记录每个采样数据的状态
status = new int[s.length];
// M个周期可以当成滑窗，l是滑窗的左边界
int l = 0;
// 滑窗内错误数据的个数
int window_fault_count = 0;
// 滑窗右边界纳入新数据
for (int r = 0; r < s.length; r++) {
// 如果滑窗长度超过了m，那么滑窗的左边界需要右移
if (r - l + 1 > m) {
// 如果右移前的，滑窗左边界对于的数据状态是FAULT，则右移后的滑窗内错误数据个数-1
if (status[l++] == FAULT) window_fault_count--;
}
// 检查数据状态
if (check_normal(r)) {
// 如果数据正常，则标记status[r]为正常状态
status[r] = NORMAL;
} else {
// 如果数据异常，则需要检查当前数据前面一个数据的状态
if (r < 1 || status[r - 1] == ABORT) {
// 如果当前数据前面一个数据的状态是丢弃的，则当前数据没有代替值，也需要被丢弃
status[r] = ABORT;
// 一旦出现丢弃数据，则滑窗中断，此时需要重置滑窗
window_fault_count = 0;
l = r + 1;
} else {
// 如果当前数据前面一个数据的状态不是丢弃状态，那么滑窗内错误数据个数+1
if (++window_fault_count < t) {
// 如果滑窗内错误数据个数没有超过阈值t，那么可以用前面一个数据代替
status[r] = FAULT;
s[r] = s[r - 1];
} else {
// 如果滑窗内错误数据个数超过了阈值t，那么 r 位置就是故障开始的位置
// 此时 r 位置数据需要被丢弃，此时滑窗中断，需要重置滑窗
status[r] = ABORT;
window_fault_count = 0;
// i 位置就是 故障恢复检查期开始位置
int i = r + 1;
// 故障恢复检查期内连续正确数据个数
int recovery_correct_count = 0;
while (i < s.length) {
if (check_recovery(i)) {
recovery_correct_count++;
status[i] = RECOVERY_NORMAL;
// 当故障恢复期间，连续正确数据个数达到p，则故障解除
if (recovery_correct_count == p) break;
} else {
recovery_correct_count = 0;
status[i] = RECOVERY_FAULT;
}
i++;
}
// i 位置是故障解除的位置，则下一次，我们应该从 i+1 位置开始重新判断，即滑窗的左、右边界都要更新为i+1
if (i < s.length) {
l = i + 1;
r = i; // 这里r没有等于 i+1，是因为for循环会给r++
}
}
}
}
}
// 最后只需要找到 status 数组中最长的连续NORMAL和FAULT即可
int maxLen = 0;
int len = 0;
for (int sta : status) {
if (sta == NORMAL || sta == FAULT) {
len++;
} else {
maxLen = Math.max(maxLen, len);
len = 0;
}
}
return Math.max(maxLen, len);
}
// 正常期间检查
public static boolean check_normal(int i) {
if (s[i] <= 0) return false; // S[i] <= 0，即为错误值
// 和前面采样数据比较的前提条件是：前面的采样数据必须是正常状态，或者正常期错误状态
if (i >= 1 && (status[i - 1] == NORMAL || status[i - 1] == FAULT)) {
if (s[i] < s[i - 1]) return false; // S[i] < S[i-1]，即为错误值
if (s[i] - s[i - 1] >= 10) return false; // S[i] - S[i-1] >= 10，即为错误值
}
return true; // 其它情况为正常值
}
// 故障恢复期检查
public static boolean check_recovery(int i) {
if (s[i] <= 0) return false; // S[i] <= 0，即为错误值
// 和前面采样数据比较的前提条件是：前面的采样数据不能时丢弃状态，以及恢复期错误状态
if (i >= 1 && status[i - 1] != ABORT && status[i - 1] != RECOVERY_FAULT) {
if (s[i] < s[i - 1]) return false; // S[i] < S[i-1]，即为错误值
if (s[i] - s[i - 1] >= 10) return false; // S[i] - S[i-1] >= 10，即为错误值
}
return true; // 其它情况为正常值
}
}
Python算法源码
# 输入获取
m, t, p = map(int, input().split()) # 故障确认周期数m, 故障次数门限t, 故障恢复周期数p
s = list(map(int, input().split())) # 一段周期的采样数据列表
# 全局变量
NORMAL = 1 # 正常数据的状态
FAULT = 2 # 错误数据的状态
ABORT = 3 # 丢弃的状态
RECOVERY_NORMAL = 4 # 故障恢复检查期间的正常数据的状态
RECOVERY_FAULT = 5 # 故障恢复检查期间的错误数据的状态
# 记录每个采样数据的状态
status = [0] * (len(s))
# 正常期间检查
def check_normal(i):
if s[i] <= 0:
return False
# 和前面采样数据比较的前提条件是：前面的采样数据必须是正常状态，或者正常期错误状态
if i >= 1 and (status[i-1] == NORMAL or status[i-1] == FAULT):
if s[i] < s[i-1]:
return False
if s[i] - s[i-1] >= 10:
return False
return True
# 故障恢复期间检查
def check_recovery(i):
if s[i] <= 0:
return False
# 和前面采样数据比较的前提条件是：前面的采样数据不能时丢弃状态，以及恢复期错误状态
if i >= 1 and status[i-1] != ABORT and status[i-1] != RECOVERY_FAULT:
if s[i] < s[i - 1]:
return False
if s[i] - s[i - 1] >= 10:
return False
return True
# 算法入口
def getResult():
# M个周期可以当成滑窗，l是滑窗的左边界, r是滑窗的右边界
l, r = 0, 0
# 滑窗内错误数据的个数
window_fault_count = 0
# 滑窗右边界纳入新数据
while r < len(s):
# 如果滑窗长度超过了m，那么滑窗的左边界需要右移
if r - l + 1 > m:
# 如果右移前的，滑窗左边界对于的数据状态是FAULT，则右移后的滑窗内错误数据个数-1
if status[l] == FAULT:
window_fault_count -= 1
l += 1
# 检查数据状态
if check_normal(r):
# 如果数据正常，则标记status[r]为正常状态
status[r] = NORMAL
else:
# 如果数据异常，则需要检查当前数据前面一个数据的状态
if r < 1 or status[r-1] == ABORT:
# 如果当前数据前面一个数据的状态是丢弃的，则当前数据没有代替值，也需要被丢弃
status[r] = ABORT
# 一旦出现丢弃数据，则滑窗中断，此时需要重置滑窗
window_fault_count = 0
l = r + 1
else:
# 如果当前数据前面一个数据的状态不是丢弃状态，那么滑窗内错误数据个数+1
window_fault_count += 1
if window_fault_count < t:
# 如果滑窗内错误数据个数没有超过阈值t，那么可以用前面一个数据代替
status[r] = FAULT
s[r] = s[r-1]
else:
# 如果滑窗内错误数据个数超过了阈值t，那么 r 位置就是故障开始的位置
# 此时 r 位置数据需要被丢弃，此时滑窗中断，需要重置滑窗
status[r] = ABORT
window_fault_count = 0
# i 位置就是 故障恢复检查期开始位置
i = r + 1
# 故障恢复检查期内连续正确数据个数
recovery_correct_count = 0
while i < len(s):
if check_recovery(i):
recovery_correct_count += 1
status[i] = RECOVERY_NORMAL
# 当故障恢复期间，连续正确数据个数达到p，则故障解除
if recovery_correct_count == p:
break
else:
recovery_correct_count = 0
status[i] = RECOVERY_FAULT
i += 1
# i 位置是故障解除的位置，则下一次，我们应该从 i+1 位置开始重新判断，即滑窗的左、右边界都要更新为i+1
if i < len(s):
l = i + 1
r = i # 这里r没有等于 i+1，是后面有while循环的r+=1
r += 1
# 最后只需要找到 status 数组中最长的连续NORMAL和FAULT即可
maxLength = 0
length = 0
for sta in status:
if sta == NORMAL or sta == FAULT:
length += 1
else:
maxLength = max(maxLength, length)
length = 0
return max(maxLength, length)
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#define MAX(a,b) a > b ? a : b
#define TRUE 1
#define FALSE 0
#define MAX_SIZE 100000
// 采样数据状态
#define NORMAL 1 // 正常数据的状态
#define FAULT 2 // 错误数据的状态
#define ABORT 3 // 丢弃的状态
#define RECOVERY_NORMAL 4 // 故障恢复检查期间的正常数据的状态
#define RECOVERY_FAULT 5 // 故障恢复检查期间的错误数据的状态
// 故障确认周期数m, 故障次数门限t, 故障恢复周期数p
int m, t, p;
// 采样数据列表
int s[MAX_SIZE];
int s_size = 0;
// 采样数据列表中各个数据的状态
int status[MAX_SIZE] = { 0 };
// 函数声明
int getResult();
int check_normal(int i);
int check_recovery(int i);
int main()
{
// 输入获取
scanf("%d %d %d", &m, &t, &p);
while (scanf("%d", &s[s_size++]))
{
if (getchar() != ' ') break;
}
printf("%dn", getResult());
return 0;
}
int getResult()
{
// M个周期可以当成滑窗，l是滑窗的左边界
int l = 0;
// 滑窗内错误数据的个数
int window_fault_count = 0;
// 滑窗右边界纳入新数据
for (int r = 0; r < s_size; r++)
{
// 如果滑窗长度超过了m，那么滑窗的左边界需要右移
if (r - l + 1 > m)
{
// 如果右移前的，滑窗左边界对于的数据状态是FAULT，则右移后的滑窗内错误数据个数-1
if (status[l++] == FAULT) window_fault_count--;
}
// 检查数据状态
if (check_normal(r))
{
// 如果数据正常，则标记status[r]为正常状态
status[r] = NORMAL;
}
else
{
// 如果数据异常，则需要检查当前数据前面一个数据的状态
if (r < 1 || status[r - 1] == ABORT)
{
// 如果当前数据前面一个数据的状态是丢弃的，则当前数据没有代替值，也需要被丢弃
status[r] = ABORT;
// 一旦出现丢弃数据，则滑窗中断，此时需要重置滑窗
window_fault_count = 0;
l = r + 1;
}
else
{
// 如果当前数据前面一个数据的状态不是丢弃状态，那么滑窗内错误数据个数+1
if (++window_fault_count < t)
{
// 如果滑窗内错误数据个数没有超过阈值t，那么可以用前面一个数据代替
status[r] = FAULT;
s[r] = s[r - 1];
}
else {
// 如果滑窗内错误数据个数超过了阈值t，那么 r 位置就是故障开始的位置
// 此时 r 位置数据需要被丢弃，此时滑窗中断，需要重置滑窗
status[r] = ABORT;
window_fault_count = 0;
// i 位置就是 故障恢复检查期开始位置
int i = r + 1;
// 故障恢复检查期内连续正确数据个数
int recovery_correct_count = 0;
while (i < s_size)
{
if (check_recovery(i))
{
recovery_correct_count++;
status[i] = RECOVERY_NORMAL;
// 当故障恢复期间，连续正确数据个数达到p，则故障解除
if (recovery_correct_count == p) break;
}
else
{
recovery_correct_count = 0;
status[i] = RECOVERY_FAULT;
}
i++;
}
// i 位置是故障解除的位置，则下一次，我们应该从 i+1 位置开始重新判断，即滑窗的左、右边界都要更新为i+1
if (i < s_size)
{
l = i + 1;
r = i; // 这里r没有等于 i+1，是因为for循环会给r++
}
}
}
}
}
// 最后只需要找到 status 数组中最长的连续NORMAL和FAULT即可
int maxLen = 0;
int len = 0;
for (int i = 0; i < s_size; i++)
{
if (status[i] == NORMAL || status[i] == FAULT)
{
len++;
}
else
{
maxLen = MAX(maxLen, len);
len = 0;
}
}
return MAX(maxLen, len);
}
// 正常期间检查
int check_normal(int i)
{
// S[i] <= 0，即为错误值
if (s[i] <= 0) return FALSE;
// 和前面采样数据比较的前提条件是：前面的采样数据必须是正常状态，或者正常期错误状态
if (i >= 1 && (status[i - 1] == NORMAL || status[i - 1] == FAULT))
{
if (s[i] < s[i - 1]) return FALSE; // S[i] < S[i-1]，即为错误值
if (s[i] - s[i - 1] >= 10) return FALSE; // S[i] - S[i-1] >= 10，即为错误值
}
return TRUE; // 其它情况为正常值
}
// 故障恢复期检查
int check_recovery(int i)
{
// S[i] <= 0，即为错误值
if (s[i] <= 0) return FALSE;
// 和前面采样数据比较的前提条件是：前面的采样数据不能时丢弃状态，以及恢复期错误状态
if (i >= 1 && status[i - 1] != ABORT && status[i - 1] != RECOVERY_FAULT)
{
if (s[i] < s[i - 1]) return FALSE; // S[i] < S[i-1]，即为错误值
if (s[i] - s[i - 1] >= 10) return FALSE; // S[i] - S[i-1] >= 10，即为错误值
}
return TRUE; // 其它情况为正常值
}免责声明：
1、IT资源小站为非营利性网站，全站所有资料仅供网友个人学习使用，禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享，本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题，请立即告知本站，本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体，但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员，一律视为同意网站规定，本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0