题目描述
"吃货"和"馋嘴"两人到披萨店点了一份铁盘(圆形)披萨,并嘱咐店员将披萨按放射状切成大小相同的偶数个小块。但是粗心的服务员将披萨切成了每块大小都完全不同奇数块,且肉眼能分辨出大小。
由于两人都想吃到最多的披萨,他们商量了一个他们认为公平的分法:从"吃货"开始,轮流取披萨。除了第一块披萨可以任意选取外,其他都必须从缺口开始选。
他俩选披萨的思路不同。"馋嘴"每次都会选最大块的披萨,而且"吃货"知道"馋嘴"的想法。
已知披萨小块的数量以及每块的大小,求"吃货"能分得的最大的披萨大小的总和。
输入描述
第 1 行为一个正整数奇数 N,表示披萨小块数量。
- 3 ≤ N < 500
接下来的第 2 行到第 N + 1 行(共 N 行),每行为一个正整数,表示第 i 块披萨的大小
- 1 ≤ i ≤ N
披萨小块从某一块开始,按照一个方向次序顺序编号为 1 ~ N
- 每块披萨的大小范围为 [1, 2147483647]
输出描述
"吃货"能分得到的最大的披萨大小的总和。
用例
| 输入 | 5 8 2 10 5 7 |
| 输出 | 19 |
| 说明 |
此例子中,有 5 块披萨。每块大小依次为 8、2、10、5、7。 按照如下顺序拿披萨,可以使"吃货"拿到最多披萨: "吃货" 拿大小为 10 的披萨 "馋嘴" 拿大小为 5 的披萨 "吃货" 拿大小为 7 的披萨 "馋嘴" 拿大小为 8 的披萨 "吃货" 拿大小为 2 的披萨 至此,披萨瓜分完毕,"吃货"拿到的披萨总大小为 10 + 7 + 2 = 19 可能存在多种拿法,以上只是其中一种。 |
题目解析
题目用例意思如下:
初始月饼如下:
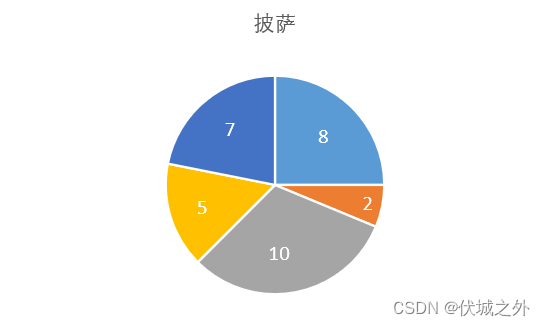
题目说
从"吃货"开始,轮流取披萨。
除了第一块披萨可以任意选取外,其他都必须从缺口开始选。
因此第一轮从"吃货"开始选,按照题目用例说明,先选走了10
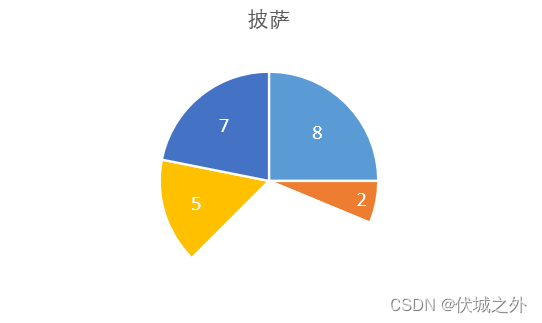
下一轮轮到"馋嘴"选,且必须从缺口的两端(5,2)中选,题目说:
"馋嘴"每次都会选最大块的披萨
因此"馋嘴"固定选择缺口的两端中较大的,即必然选走5
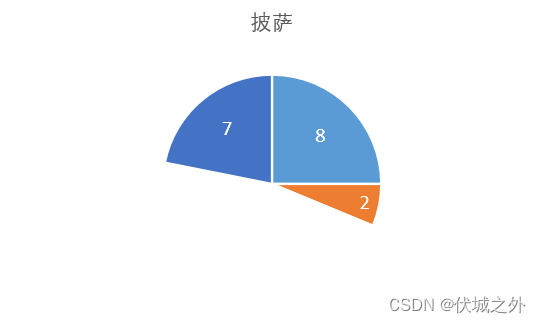
下一轮轮到吃货选择,而吃货也必须从缺口两端(7,2)中选:
- 如果选走2的话,那么下一轮,馋嘴肯定选走8
- 如果选走7的话,那么下一轮,馋嘴肯定选走8
因此无论吃货无论选哪个,馋嘴下一轮肯定选走8,因此吃货此轮选走7更优
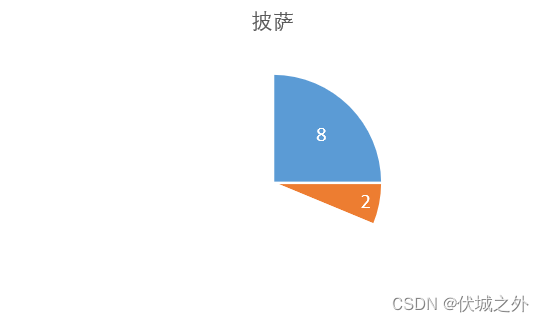
下一轮轮到馋嘴选,肯定选走8
最后一轮吃货再选走2。
本题我的解题思路是利用递归来求解。
第一轮,"吃货"可以拿任意一块披萨。而"吃货"拿完后,披萨铁盘就会产生缺口,而"馋嘴"取走披萨是明确的,就是缺口左右两边中较大者。
第二轮,"吃货"需要从披萨铁盘的缺口处选择,有两种:
- 选择缺口左边的披萨
- 选择缺口右边的披萨
此时我们可以进行递归开两个分支,分别去尝试此轮取左边,和此轮取右边,最终选取两种方式中可以给"吃货"带来最大披萨大小的那个值。
而一旦"吃货"选完,"馋嘴"选取的披萨是明确的,即缺口左右两边中较大值。
第三轮,"吃货"的选取披萨策略,继续按照第二轮的方式进行递归处理
…..
第X轮,只剩一块披萨时,由于披萨一开始就分成了奇数块,而"吃货"又有先选优势,因此最后一块也是"吃货"的,此时结束递归。
本题的披萨数量 3 ≤ N < 500,这个数量级依赖纯递归,会超时。
因此我们可以加入缓存优化,即将某个缺口状态下,"吃货"能获得的最大披萨大小记录下来,比如:

上图所示中,披萨的缺口状态是 [左边7, 右边2],且当前状态处于"吃货"选择的轮次,我们按照前面思路可以知道这种缺口状态下,"吃货"能得到的最大披萨为 7 + 2
因此:
假设左边缺口位置是 L,右边缺口位置是 R
那么可以记录下:cache[L][R] = 7 + 2
如果后面再次遇到上面缺口状态,则无需重新递归计算,只需要取出cache[L][R]即可。
递归的缓存优化策略很常见,比如斐波那契数列的求解。大家可以找找相关资料熟悉下。
另外Python有针对函数结果的自动缓存标签@cache,可以避免手动实现缓存表,实现上更佳简单
JS算法源码
纯递归(会超时,但是是下一种解法的基础,需要先看懂这里)
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
// 披萨数量(奇数个)
const n = parseInt(await readline());
// n个披萨的大小(各不相同)
const pizza = [];
for (let i = 0; i < n; i++) {
pizza.push(parseInt(await readline()));
}
function check(idx) {
if (idx < 0) {
idx = n - 1;
} else if (idx >= n) {
idx = 0;
}
return idx;
}
function recursive(l, r) {
// 进入递归前,"吃货"已经拿了披萨,因此进入递归后,轮到"馋嘴"拿
// 而"馋嘴"拿披萨的策略固定是:缺口左右两边中较大的那块
if (pizza[l] > pizza[r]) {
// 拿走第 l 块,因此缺口左边的位置变为 l - 1
l = check(l - 1);
} else {
// 拿走第 r 块,因此缺口右边的位置变为 r + 1
r = check(r + 1);
}
if (l == r) {
// 当 l == r 是,说明只剩一块披萨了,由于奇数个披萨,且"吃货"第一个拿,因此最后一个也是"吃货"拿
return pizza[l];
} else {
// 如果还剩多块披萨,那么"吃货"有两种选择:
// 1、拿缺口左边的披萨
// 2、拿缺口右边的披萨
// 因此这里直接开两个递归分支,最终结果取较大值
return Math.max(
recursive(check(l - 1), r) + pizza[l],
recursive(l, check(r + 1)) + pizza[r]
);
}
}
// ans记录"吃货"能获得的最大披萨大小
let ans = 0;
// i 指向首轮被"吃货"选取的披萨位置,可以理解为缺口位置,相当于给环切了一个口
for (let i = 0; i < n; i++) {
// i - 1 是缺口的左边披萨,check函数作用是防止 i - 1 越界, 进行绕环运动
// i + 1 是缺口的右边披萨,check函数作用是防止 i + 1 越界,进行绕环运动
// recursive的作用求解是"吃货"从缺失了 第 i 块的披萨铁盘 开始选,最终可得的最大披萨大小,
// 而第 i 块是首轮就被"吃货"拿走的,因此是recursive + pizza[i]
ans = Math.max(ans, recursive(check(i - 1), check(i + 1)) + pizza[i]);
}
console.log(ans);
})();
递归 + 缓存(不超时)
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const n = parseInt(await readline());
const pizza = [];
for (let i = 0; i < n; i++) {
pizza.push(parseInt(await readline()));
}
// 缓存
const cache = new Array(n).fill(0).map(() => new Array(n).fill(0));
function check(idx) {
if (idx < 0) {
idx = n - 1;
} else if (idx >= n) {
idx = 0;
}
return idx;
}
function recursive(l, r) {
if (pizza[l] > pizza[r]) {
l = check(l - 1);
} else {
r = check(r + 1);
}
// 缓存优化,如果对应缺口状态的披萨铁盘结果已经算过了,则无需再次重复递归
if (cache[l][r] > 0) {
return cache[l][r];
}
if (l == r) {
// 缓存对应缺口状态下,吃货可得的最大披萨大小
cache[l][r] = pizza[l];
} else {
// 缓存对应缺口状态下,吃货可得的最大披萨大小
cache[l][r] = Math.max(
recursive(check(l - 1), r) + pizza[l],
recursive(l, check(r + 1)) + pizza[r]
);
}
return cache[l][r];
}
let ans = 0;
for (let i = 0; i < n; i++) {
ans = Math.max(ans, recursive(check(i - 1), check(i + 1)) + pizza[i]);
}
console.log(ans);
})();
Java算法源码
纯递归(会超时,但是是下一种解法的基础,需要先看懂这里)
import java.util.Scanner;
public class Main {
static int[] pizza;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 披萨数量(奇数个)
int n = sc.nextInt();
// n个披萨的大小(各不相同)
pizza = new int[n];
for (int i = 0; i < n; i++) {
pizza[i] = sc.nextInt();
}
// ans记录"吃货"能获得的最大披萨大小
long ans = 0;
// i 指向首轮被"吃货"选取的披萨位置,可以理解为缺口位置,相当于给环切了一个口
for (int i = 0; i < n; i++) {
// i - 1 是缺口的左边披萨,check函数作用是防止 i - 1 越界, 进行绕环运动
// i + 1 是缺口的右边披萨,check函数作用是防止 i + 1 越界,进行绕环运动
// recursive的作用求解是"吃货"从缺失了 第 i 块的披萨铁盘 开始选,最终可得的最大披萨大小,
// 而第 i 块是首轮就被"吃货"拿走的,因此是recursive + pizza[i]
ans = Math.max(ans, recursive(check(i - 1), check(i + 1)) + pizza[i]);
}
System.out.println(ans);
}
public static long recursive(int l, int r) {
// 进入递归前,"吃货"已经拿了披萨,因此进入递归后,轮到"馋嘴"拿
// 而"馋嘴"拿披萨的策略固定是:缺口左右两边中较大的那块
if (pizza[l] > pizza[r]) { // 注意披萨大小各部相同,因此要么左边大,要么右边大,不存在相等的情况
// 拿走第 l 块,因此缺口左边的位置变为 l - 1
l = check(l - 1);
} else {
// 拿走第 r 块,因此缺口右边的位置变为 r + 1
r = check(r + 1);
}
if (l == r) {
// 当 l == r 是,说明只剩一块披萨了,由于奇数个披萨,且"吃货"第一个拿,因此最后一个也是"吃货"拿
return pizza[l];
} else {
// 如果还剩多块披萨,那么"吃货"有两种选择:
// 1、拿缺口左边的披萨
// 2、拿缺口右边的披萨
// 因此这里直接开两个递归分支,最终结果取较大值
return Math.max(recursive(check(l - 1), r) + pizza[l], recursive(l, check(r + 1)) + pizza[r]);
}
}
public static int check(int idx) {
if (idx < 0) {
idx = pizza.length - 1;
} else if (idx >= pizza.length) {
idx = 0;
}
return idx;
}
}
递归 + 缓存(不超时)
import java.util.Scanner;
public class Main {
static int[] pizza;
// 缓存
static long[][] cache;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
pizza = new int[n];
for (int i = 0; i < n; i++) {
pizza[i] = sc.nextInt();
}
// 缓存
cache = new long[n][n];
long ans = 0;
for (int i = 0; i < n; i++) {
ans = Math.max(ans, recursive(check(i - 1), check(i + 1)) + pizza[i]);
}
System.out.println(ans);
}
public static long recursive(int l, int r) {
if (pizza[l] > pizza[r]) {
l = check(l - 1);
} else {
r = check(r + 1);
}
// 缓存优化,如果对应缺口状态的披萨铁盘结果已经算过了,则无需再次重复递归
if (cache[l][r] > 0) {
return cache[l][r];
}
if (l == r) {
// 缓存对应缺口状态下,吃货可得的最大披萨大小
cache[l][r] = pizza[l];
} else {
// 缓存对应缺口状态下,吃货可得的最大披萨大小
cache[l][r] =
Math.max(recursive(check(l - 1), r) + pizza[l], recursive(l, check(r + 1)) + pizza[r]);
}
return cache[l][r];
}
public static int check(int idx) {
if (idx < 0) {
idx = pizza.length - 1;
} else if (idx >= pizza.length) {
idx = 0;
}
return idx;
}
}
Python算法源码
纯递归(会超时,但是是下一种解法的基础,需要先看懂这里)
# 输入获取
n = int(input()) # 披萨数量(奇数个)
pizza = [] # n个披萨的大小(各不相同)
for _ in range(n):
pizza.append(int(input()))
# 越界索引环形变化
def check(idx):
if idx < 0:
idx = n - 1
elif idx >= n:
idx = 0
return idx
def recursive(l, r):
# 进入递归前,"吃货"已经拿了披萨,因此进入递归后,轮到"馋嘴"拿
# 而"馋嘴"拿披萨的策略固定是:缺口左右两边中较大的那块
if pizza[l] > pizza[r]: # 注意披萨大小各部相同,因此要么左边大,要么右边大,不存在相等的情况
# 拿走第 l 块,因此缺口左边的位置变为 l - 1
l = check(l - 1)
else:
# 拿走第 r 块,因此缺口右边的位置变为 r + 1
r = check(r + 1)
if l == r:
# 当 l == r 是,说明只剩一块披萨了,由于奇数个披萨,且"吃货"第一个拿,因此最后一个也是"吃货"拿
return pizza[l]
else:
# 如果还剩多块披萨,那么"吃货"有两种选择:
# 1、拿缺口左边的披萨
# 2、拿缺口右边的披萨
# 因此这里直接开两个递归分支,最终结果取较大值
return max(recursive(check(l - 1), r) + pizza[l], recursive(l, check(r + 1)) + pizza[r])
def getResult():
# ans记录"吃货"能获得的最大披萨大小
ans = 0
# i 指向首轮被"吃货"选取的披萨位置,可以理解为缺口位置,相当于给环切了一个口
for i in range(n):
# i - 1 是缺口的左边披萨,check函数作用是防止 i - 1 越界, 进行绕环运动
# i + 1 是缺口的右边披萨,check函数作用是防止 i + 1 越界,进行绕环运动
# recursive的作用求解是"吃货"从缺失了 第 i 块的披萨铁盘 开始选,最终可得的最大披萨大小,
# 而第 i 块是首轮就被"吃货"拿走的,因此是recursive + pizza[i]
ans = max(ans, recursive(check(i - 1), check(i + 1)) + pizza[i])
return ans
print(getResult())
递归 + 手动缓存(不超时)(下面还有一个自动缓存标签,代码更简单)
# 输入获取
n = int(input()) # 披萨数量(奇数个)
pizza = [] # n个披萨的大小(各不相同)
for _ in range(n):
pizza.append(int(input()))
# 缓存表
cache = [[0] * n for _ in range(n)]
# 越界索引环形变化
def check(idx):
if idx < 0:
idx = n - 1
elif idx >= n:
idx = 0
return idx
def recursive(l, r):
# 进入递归前,"吃货"已经拿了披萨,因此进入递归后,轮到"馋嘴"拿
# 而"馋嘴"拿披萨的策略固定是:缺口左右两边中较大的那块
if pizza[l] > pizza[r]: # 注意披萨大小各部相同,因此要么左边大,要么右边大,不存在相等的情况
# 拿走第 l 块,因此缺口左边的位置变为 l - 1
l = check(l - 1)
else:
# 拿走第 r 块,因此缺口右边的位置变为 r + 1
r = check(r + 1)
if cache[l][r] > 0:
return cache[l][r]
if l == r:
# 当 l == r 是,说明只剩一块披萨了,由于奇数个披萨,且"吃货"第一个拿,因此最后一个也是"吃货"拿
cache[l][r] = pizza[l]
else:
# 如果还剩多块披萨,那么"吃货"有两种选择:
# 1、拿缺口左边的披萨
# 2、拿缺口右边的披萨
# 因此这里直接开两个递归分支,最终结果取较大值
cache[l][r] = max(recursive(check(l - 1), r) + pizza[l], recursive(l, check(r + 1)) + pizza[r])
return cache[l][r]
def getResult():
# ans记录"吃货"能获得的最大披萨大小
ans = 0
# i 指向首轮被"吃货"选取的披萨位置,可以理解为缺口位置,相当于给环切了一个口
for i in range(n):
# i - 1 是缺口的左边披萨,check函数作用是防止 i - 1 越界, 进行绕环运动
# i + 1 是缺口的右边披萨,check函数作用是防止 i + 1 越界,进行绕环运动
# recursive的作用求解是"吃货"从缺失了 第 i 块的披萨铁盘 开始选,最终可得的最大披萨大小,
# 而第 i 块是首轮就被"吃货"拿走的,因此是recursive + pizza[i]
ans = max(ans, recursive(check(i - 1), check(i + 1)) + pizza[i])
return ans
print(getResult())
递归 + 自动缓存(利用python的@cache标签实现自动函数结果缓存)
from functools import cache
# 输入获取
n = int(input()) # 披萨数量(奇数个)
pizza = [] # n个披萨的大小(各不相同)
for _ in range(n):
pizza.append(int(input()))
# 越界索引环形变化
def check(idx):
if idx < 0:
idx = n - 1
elif idx >= n:
idx = 0
return idx
@cache
def recursive(l, r):
# 进入递归前,"吃货"已经拿了披萨,因此进入递归后,轮到"馋嘴"拿
# 而"馋嘴"拿披萨的策略固定是:缺口左右两边中较大的那块
if pizza[l] > pizza[r]: # 注意披萨大小各部相同,因此要么左边大,要么右边大,不存在相等的情况
# 拿走第 l 块,因此缺口左边的位置变为 l - 1
l = check(l - 1)
else:
# 拿走第 r 块,因此缺口右边的位置变为 r + 1
r = check(r + 1)
if l == r:
# 当 l == r 是,说明只剩一块披萨了,由于奇数个披萨,且"吃货"第一个拿,因此最后一个也是"吃货"拿
return pizza[l]
else:
# 如果还剩多块披萨,那么"吃货"有两种选择:
# 1、拿缺口左边的披萨
# 2、拿缺口右边的披萨
# 因此这里直接开两个递归分支,最终结果取较大值
return max(recursive(check(l - 1), r) + pizza[l], recursive(l, check(r + 1)) + pizza[r])
def getResult():
# ans记录"吃货"能获得的最大披萨大小
ans = 0
# i 指向首轮被"吃货"选取的披萨位置,可以理解为缺口位置,相当于给环切了一个口
for i in range(n):
# i - 1 是缺口的左边披萨,check函数作用是防止 i - 1 越界, 进行绕环运动
# i + 1 是缺口的右边披萨,check函数作用是防止 i + 1 越界,进行绕环运动
# recursive的作用求解是"吃货"从缺失了 第 i 块的披萨铁盘 开始选,最终可得的最大披萨大小,
# 而第 i 块是首轮就被"吃货"拿走的,因此是recursive + pizza[i]
ans = max(ans, recursive(check(i - 1), check(i + 1)) + pizza[i])
return ans
print(getResult())
C算法源码
纯递归(会超时,但是是下一种解法的基础,需要先看懂这里)
#include <stdio.h>
#define MAX(a, b) ((a) > (b) ? (a) : (b))
int pizza_size; // 披萨数量(奇数个)
int pizza[500]; // n个披萨的大小(各不相同)
// 越界索引环形走位
int check(int idx) {
if (idx < 0) {
idx = pizza_size - 1;
} else if (idx >= pizza_size) {
idx = 0;
}
return idx;
}
long long recursive(int l, int r) {
// 进入递归前,"吃货"已经拿了披萨,因此进入递归后,轮到"馋嘴"拿
// 而"馋嘴"拿披萨的策略固定是:缺口左右两边中较大的那块
if (pizza[l] > pizza[r]) { // 注意披萨大小各部相同,因此要么左边大,要么右边大,不存在相等的情况
// 拿走第 l 块,因此缺口左边的位置变为 l - 1
l = check(l - 1);
} else {
// 拿走第 r 块,因此缺口右边的位置变为 r + 1
r = check(r + 1);
}
if (l == r) {
// 当 l == r 是,说明只剩一块披萨了,由于奇数个披萨,且"吃货"第一个拿,因此最后一个也是"吃货"拿
return pizza[l];
} else {
// 如果还剩多块披萨,那么"吃货"有两种选择:
// 1、拿缺口左边的披萨
long long v1 = recursive(check(l - 1), r) + pizza[l];
// 2、拿缺口右边的披萨
long long v2 = recursive(l, check(r + 1)) + pizza[r];
// 因此这里直接开两个递归分支,最终结果取较大值
return MAX(v1, v2);
}
}
int main() {
scanf("%d", &pizza_size);
for (int i = 0; i < pizza_size; i++) {
scanf("%d", &pizza[i]);
}
// ans记录"吃货"能获得的最大披萨大小
long long ans = 0;
// i 指向首轮被"吃货"选取的披萨位置,可以理解为缺口位置,相当于给环切了一个口
for (int i = 0; i < pizza_size; i++) {
// i - 1 是缺口的左边披萨,check函数作用是防止 i - 1 越界, 进行绕环运动
// i + 1 是缺口的右边披萨,check函数作用是防止 i + 1 越界,进行绕环运动
// recursive的作用求解是"吃货"从缺失了 第 i 块的披萨铁盘 开始选,最终可得的最大披萨大小,
// 而第 i 块是首轮就被"吃货"拿走的,因此是recursive + pizza[i]
long long v = recursive(check(i - 1), check(i + 1)) + pizza[i];
ans = MAX(ans, v);
}
printf("%lldn", ans);
return 0;
}递归 + 缓存(不超时)
#include <stdio.h>
#define MAX(a, b) ((a) > (b) ? (a) : (b))
int pizza_size; // 披萨数量(奇数个)
int pizza[500]; // n个披萨的大小(各不相同)
long long cache[500][500];
// 越界索引环形走位
int check(int idx) {
if (idx < 0) {
idx = pizza_size - 1;
} else if (idx >= pizza_size) {
idx = 0;
}
return idx;
}
long long recursive(int l, int r) {
// 进入递归前,"吃货"已经拿了披萨,因此进入递归后,轮到"馋嘴"拿
// 而"馋嘴"拿披萨的策略固定是:缺口左右两边中较大的那块
if (pizza[l] > pizza[r]) { // 注意披萨大小各部相同,因此要么左边大,要么右边大,不存在相等的情况
// 拿走第 l 块,因此缺口左边的位置变为 l - 1
l = check(l - 1);
} else {
// 拿走第 r 块,因此缺口右边的位置变为 r + 1
r = check(r + 1);
}
if(cache[l][r] > 0) {
return cache[l][r];
}
if (l == r) {
// 当 l == r 是,说明只剩一块披萨了,由于奇数个披萨,且"吃货"第一个拿,因此最后一个也是"吃货"拿
cache[l][r] = pizza[l];
} else {
// 如果还剩多块披萨,那么"吃货"有两种选择:
// 1、拿缺口左边的披萨
long long v1 = recursive(check(l - 1), r) + pizza[l];
// 2、拿缺口右边的披萨
long long v2 = recursive(l, check(r + 1)) + pizza[r];
// 因此这里直接开两个递归分支,最终结果取较大值
cache[l][r] = MAX(v1, v2);
}
return cache[l][r];
}
int main() {
scanf("%d", &pizza_size);
for (int i = 0; i < pizza_size; i++) {
scanf("%d", &pizza[i]);
}
// ans记录"吃货"能获得的最大披萨大小
long long ans = 0;
// i 指向首轮被"吃货"选取的披萨位置,可以理解为缺口位置,相当于给环切了一个口
for (int i = 0; i < pizza_size; i++) {
// i - 1 是缺口的左边披萨,check函数作用是防止 i - 1 越界, 进行绕环运动
// i + 1 是缺口的右边披萨,check函数作用是防止 i + 1 越界,进行绕环运动
// recursive的作用求解是"吃货"从缺失了 第 i 块的披萨铁盘 开始选,最终可得的最大披萨大小,
// 而第 i 块是首轮就被"吃货"拿走的,因此是recursive + pizza[i]
long long v = recursive(check(i - 1), check(i + 1)) + pizza[i];
ans = MAX(ans, v);
}
printf("%lldn", ans);
return 0;
}免责声明:
评论0