题目描述
从前有个村庄,村民们喜欢在各种田地上插上小旗子,旗子上标识了各种不同的数字。
某天集体村民决定将覆盖相同数字的最小矩阵形的土地分配给村里做出巨大贡献的村民,请问此次分配土地,做出贡献的村民种最大会分配多大面积?
输入描述
第一行输入 m 和 n,
- m 代表村子的土地的长
- n 代表土地的宽
第二行开始输入地图上的具体标识
输出描述
此次分配土地,做出贡献的村民种最大会分配多大面积
备注
- 旗子上的数字为1~500,土地边长不超过500
- 未插旗子的土地用0标识
用例
| 输入 | 3 3 1 0 1 0 0 0 0 1 0 |
| 输出 | 9 |
| 说明 | 土地上的旗子为1,其坐标分别为(0,0),(2,1)以及(0,2),为了覆盖所有旗子,矩阵需要覆盖的横坐标为0和2,纵坐标为0和2,所以面积为9,即(2-0+1)*(2-0+1)= 9 |
| 输入 | 3 3 1 0 2 0 0 0 0 3 4 |
| 输出 | 1 |
| 说明 | 由于不存在成对的小旗子,故而返回1,即一块土地的面积。 |
题目解析
根据用例1说明来看,最小矩形需要覆盖相同数字得所有旗子。
土地上的旗子为1,其坐标分别为(0,0),(2,1)以及(0,2),为了覆盖所有旗子,矩阵需要覆盖的横坐标为0和2,纵坐标为0和2,所以面积为9,即(2-0+1)*(2-0+1)= 9
但是这产生一个问题?比如下图所示:
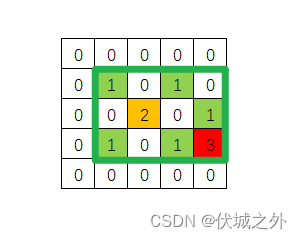
如果我要覆盖住所有的数字1,那么必然会同时覆盖了数字2,3,此时该怎么办呢?
题目没有说怎么处理,那么我理解就不需要管,只需要保证覆盖所有1的矩形最小就行。
本题解题思路很简单,只需要统计出相同数字的出现的“所有坐标位置”中:
- 最小的横坐标(矩形最上面一行的行号)
- 最大的横坐标(矩形最下面一行的行号)
- 最小的纵坐标(矩形最左边一列的列号)
- 最大的纵坐标(矩形最右边一列的列号)
即可。比如:前面图示中数字1的所有坐标位置(1,1)、(1,3)、(2,4)、(3,1)、(3,3)中:
- 最小的横坐标:1
- 最大的横坐标:3
- 最小的纵坐标:1
- 最大的纵坐标:4
那么包含所有数字1的最小矩形面积为:
(最大的横坐标 – 最小的横坐标 + 1) * (最大的纵坐标 – 最小的纵坐标 + 1)
JavaScript算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
class Rect {
constructor() {
this.minRow = Infinity;
this.maxRow = -Infinity;
this.minCol = Infinity;
this.maxCol = -Infinity;
}
setRow(row) {
this.minRow = Math.min(this.minRow, row);
this.maxRow = Math.max(this.maxRow, row);
}
setCol(col) {
this.minCol = Math.min(this.minCol, col);
this.maxCol = Math.max(this.maxCol, col);
}
}
// 长(行数)、宽(列数)
const [m, n] = (await readline()).split(" ").map(Number);
const rects = {};
for (let i = 0; i < m; i++) {
const nums = (await readline()).split(" ").map(Number);
for (let j = 0; j < n; j++) {
const num = nums[j];
if (num > 0) {
if (!rects[num]) rects[num] = new Rect();
rects[num].setRow(i);
rects[num].setCol(j);
}
}
}
let maxArea = 0;
for (let num in rects) {
const rect = rects[num];
maxArea = Math.max(
maxArea,
(rect.maxRow - rect.minRow + 1) * (rect.maxCol - rect.minCol + 1)
);
}
console.log(maxArea);
})();
Java算法源码
import java.util.HashMap;
import java.util.Scanner;
public class Main {
static class Rect {
int minRow = Integer.MAX_VALUE;
int maxRow = Integer.MIN_VALUE;
int minCol = Integer.MAX_VALUE;
int maxCol = Integer.MIN_VALUE;
private void setRow(int row) {
this.minRow = Math.min(this.minRow, row);
this.maxRow = Math.max(this.maxRow, row);
}
private void setCol(int col) {
this.minCol = Math.min(this.minCol, col);
this.maxCol = Math.max(this.maxCol, col);
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt(); // 长(行数)
int n = sc.nextInt(); // 宽(列数)
HashMap<Integer, Rect> rects = new HashMap<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int num = sc.nextInt();
if (num > 0) {
rects.putIfAbsent(num, new Rect());
rects.get(num).setRow(i);
rects.get(num).setCol(j);
}
}
}
int maxArea = 0;
for (int num : rects.keySet()) {
Rect rect = rects.get(num);
maxArea =
Math.max(maxArea, (rect.maxRow - rect.minRow + 1) * (rect.maxCol - rect.minCol + 1));
}
System.out.println(maxArea);
}
}
Python算法源码
import sys
class Rect:
def __init__(self):
self.minRow = sys.maxsize
self.maxRow = -sys.maxsize
self.minCol = sys.maxsize
self.maxCol = -sys.maxsize
def setRow(self, row):
self.minRow = min(self.minRow, row)
self.maxRow = max(self.maxRow, row)
def setCol(self, col):
self.minCol = min(self.minCol, col)
self.maxCol = max(self.maxCol, col)
# 输入获取
m, n = map(int, input().split())
rects = {}
for i in range(m):
nums = list(map(int, input().split()))
for j in range(n):
num = nums[j]
if num > 0:
rects.setdefault(num, Rect())
rects[num].setRow(i)
rects[num].setCol(j)
maxArea = 0
for num in rects:
rect = rects[num]
maxArea = max(maxArea, (rect.maxRow - rect.minRow + 1) * (rect.maxCol - rect.minCol + 1))
print(maxArea)
C算法源码
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define MIN(a, b) ((a) < (b) ? (a) : (b))
#define MAX(a, b) ((a) > (b) ? (a) : (b))
#define MAX_SIZE 500
typedef struct {
int minRow;
int maxRow;
int minCol;
int maxCol;
} Rect;
Rect *new_Rect() {
Rect *rect = (Rect *) malloc(sizeof(Rect));
rect->minRow = INT_MAX;
rect->maxRow = INT_MIN;
rect->minCol = INT_MAX;
rect->maxCol = INT_MIN;
return rect;
}
void setRow(Rect *rect, int row) {
rect->minRow = MIN(rect->minRow, row);
rect->maxRow = MAX(rect->maxRow, row);
}
void setCol(Rect *rect, int col) {
rect->minCol = MIN(rect->minCol, col);
rect->maxCol = MAX(rect->maxCol, col);
}
int main() {
int m, n;
scanf("%d %d", &m, &n);
Rect *rects[MAX_SIZE] = {NULL};
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int num;
scanf("%d", &num);
if (num > 0) {
if (rects[num] == NULL) {
rects[num] = new_Rect();
}
setRow(rects[num], i);
setCol(rects[num], j);
}
}
}
int maxArea = 0;
for (int i = 0; i < MAX_SIZE; i++) {
Rect *rect = rects[i];
if (rects[i] != NULL) {
int area = (rect->maxRow - rect->minRow + 1) * (rect->maxCol - rect->minCol + 1);
maxArea = MAX(maxArea, area);
}
}
printf("%dn", maxArea);
return 0;
}免责声明:
1、IT资源小站为非营利性网站,全站所有资料仅供网友个人学习使用,禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享,本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题,请立即告知本站,本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体,但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员,一律视为同意网站规定,本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0