题目描述
如果3个正整数(a,b,c)满足a^2 + b^2 = c^2的关系,则称(a,b,c)为勾股数(著名的勾三股四弦五),
为了探索勾股数的规律,我们定义如果勾股数(a,b,c)之间两两互质(即a与b,a与c,b与c之间均互质,没有公约数),则其为勾股数元组(例如(3,4,5)是勾股数元组,(6,8,10)则不是勾股数元组)。
请求出给定范围[N,M]内,所有的勾股数元组。
输入描述
起始范围N,1 <= N <= 10000
结束范围M,N < M <= 10000
输出描述
1. a,b,c请保证a < b < c,输出格式:a b c;
2. 多组勾股数元组请按照a升序,b升序,最后c升序的方式排序输出;
3. 给定范围中如果找不到勾股数元组时,输出”NA“。
用例
| 输入 |
1 20 |
| 输出 | 3 4 5 5 12 13 8 15 17 |
| 说明 |
[1,20]范围内勾股数有:(3 4 5),(5 12 13),(6 8 10),(8 15 17),(9 12 15),(12 16 20); 其中,满足(a,b,c)之间两两互质的勾股数元组有:(3 4 5),(5 12 13),(8 15 17); 按输出描述中顺序要求输出结果。 |
| 输入 |
5 10 |
| 输出 | NA |
| 说明 |
[5,10]范围内勾股数有:(6 8 10); 其中,没有满足(a,b,c)之间两两互质的勾股数元组; 给定范围中找不到勾股数元组,输出”NA“ |
题目解析
本题首先需要找出给定区间内的所有勾股数,当找出勾股数后,继续判断勾股数两两之间是否互质,若否,则丢弃,若是,则保留。
最终保留的就是勾股数元组。
因此本题难点有二:1、如何找出所有勾股数; 2、如何判断两个数互质
关于1,我们可以先求出区间[n,m]的所有数的平方,缓存到一个数组arr中,然后对该数组进行双重for遍历,外层遍历所有元素arr[i],内层遍历i之后的每一个元素arr[j],我们求arr[i]+arr[j]的和sum,看arr中是否包含sum元素,若是,则就得到一组勾股数sqrt(arr[i])、sqrt(arr[j])、sqrt(sum)。
按照上面逻辑求得所有勾股数。
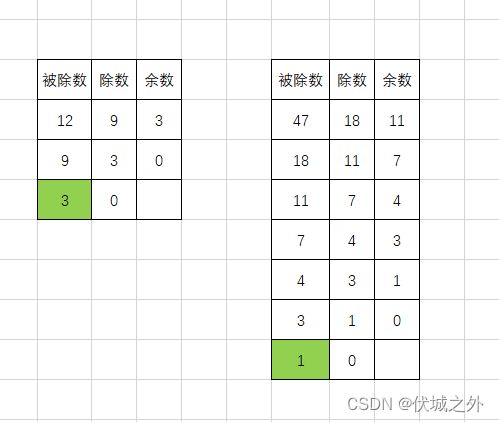
之后,我们可以根据辗转相除法判断两个数是否互质,比如求9和12是否互质,以及求47和18是否互质。
我们只需要用
a % b 得到一个 mod
然后将
a <= b
b <= mod
如果进行到b===0时,则看此时a的值,若a===1,则说明初始时的a,b互质,否则就有最大公约数结束时的a。
如下图所示:
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
const [n, m] = lines.map(Number);
getResult(n, m);
lines.length = 0;
}
});
function getResult(n, m) {
const arr = [];
for (let i = n; i <= m; i++) {
arr.push(i * i);
}
const set = new Set(arr);
const res = [];
for (let i = 0; i < arr.length; i++) {
for (let j = i + 1; j < arr.length; j++) {
/* 判断勾股数 a^2 + b^2 = c^2 */
const sum = arr[i] + arr[j];
if (set.has(sum)) {
res.push([Math.sqrt(arr[i]), Math.sqrt(arr[j]), Math.sqrt(sum)]);
}
}
}
const ans = res.filter((group) => {
const [a, b, c] = group;
return (
isRelativePrime(a, b) && isRelativePrime(a, c) && isRelativePrime(b, c)
);
});
if (!ans.length) return console.log("NA");
ans.forEach((g) => console.log(g.join(" ")));
}
/* 判断两个数是否互质,辗转相除 */
function isRelativePrime(x, y) {
while (y > 0) {
let mod = x % y;
x = y;
y = mod;
}
return x === 1;
}
Java算法源码
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Scanner;
import java.util.stream.Collectors;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
getResult(n, m);
}
public static void getResult(int n, int m) {
ArrayList<Integer> arr = new ArrayList<>();
for (int i = n; i <= m; i++) {
arr.add(i * i);
}
HashSet<Integer> set = new HashSet<>(arr);
ArrayList<Integer[]> res = new ArrayList<>();
for (int i = 0; i < arr.size(); i++) {
for (int j = i + 1; j < arr.size(); j++) {
// 判断勾股数 a^2 + b^2 = c^2
int sum = arr.get(i) + arr.get(j);
if (set.contains(sum)) {
res.add(
new Integer[] {
(int) Math.sqrt(arr.get(i)), (int) Math.sqrt(arr.get(j)), (int) Math.sqrt(sum)
});
}
}
}
List<Integer[]> collect =
res.stream()
.filter(
g ->
isRelativePrime(g[0], g[1])
&& isRelativePrime(g[0], g[2])
&& isRelativePrime(g[1], g[2]))
.collect(Collectors.toList());
if (collect.size() == 0) {
System.out.println("NA");
} else {
for (Integer[] g : collect) {
System.out.println(g[0] + " " + g[1] + " " + g[2]);
}
}
}
// 判断两个数是否互质,辗转相除
public static boolean isRelativePrime(int x, int y) {
while (y > 0) {
int mod = x % y;
x = y;
y = mod;
}
return x == 1;
}
}
Python算法源码
import math
# 输入获取
n = int(input())
m = int(input())
# 判断两个数是否互质,辗转相除
def isRelativePrime(x, y):
while y > 0:
mod = x % y
x = y
y = mod
return x == 1
# 算法入口
def getResult():
arr = []
for i in range(n, m + 1):
arr.append(i * i)
setArr = set(arr)
res = []
for i in range(len(arr)):
for j in range(i + 1, len(arr)):
# 判断勾股数 a^2 + b^2 = c^2
sumV = arr[i] + arr[j]
if sumV in setArr:
res.append([int(math.sqrt(arr[i])), int(math.sqrt(arr[j])), int(math.sqrt(sumV))])
ans = list(
filter(lambda x: isRelativePrime(x[0], x[1]) and isRelativePrime(x[0], x[2]) and isRelativePrime(x[1], x[2]),
res))
if len(ans) == 0:
print("NA")
else:
for g in ans:
print(" ".join(map(str, g)))
# 算法调用
getResult()
更高效的求解互质勾股数组的方法
互质勾股数组存在如下定理:

而本题要在范围[n, m]中选取出所有互质的勾股数元组,我们假设存在x, y,且(x > y)可以推导出互质的勾股数三元组(a, b, c)
其中:
- a = x^2 – y^2
- b = 2 * x * y
- c = x^2 + y^2
而 n <= a,b < c <= m
因此,可以继续推导出x,y的取值范围:
a + c = 2 * x^2 <= 2 * m
即 x <= sqrt(m)
c – a = 2 * y^2,其中c > a,因此c – a > 0
即 y > 0
而 x > y,因此x,y取值范围是
0 < y < x <= sqrt(m)
另外,想要通过x,y推导出的勾股数三元组a,b,c互质,则x,y必然互质,且x,y必然一个是奇数,一个是偶数。
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
const [n, m] = lines.map(Number);
getResult(n, m);
lines.length = 0;
}
});
function getResult(n, m) {
const ans = [];
const k = Math.ceil(Math.sqrt(m));
for (let y = 1; y < k; y++) {
for (let x = y + 1; x < k; x++) {
if (isRelativePrime(x, y) && (x + y) % 2 == 1) {
const a = x * x - y * y;
const b = 2 * x * y;
const c = x * x + y * y;
if (a >= n && b >= n && c <= m) {
ans.push(a < b ? [a, b, c] : [b, a, c]);
}
}
}
}
if (ans.length > 0) {
ans.sort((a, b) =>
a[0] != b[0] ? a[0] - b[0] : a[1] != b[1] ? a[1] - b[1] : a[2] - b[2]
);
for (let arr of ans) {
console.log(arr.join(" "));
}
} else {
console.log("NA");
}
}
/* 判断两个数是否互质,辗转相除 */
function isRelativePrime(x, y) {
while (y > 0) {
let mod = x % y;
x = y;
y = mod;
}
return x === 1;
}
Java算法源码
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
getResult(n, m);
}
public static void getResult(int n, int m) {
ArrayList<int[]> ans = new ArrayList<>();
int k = (int) Math.ceil(Math.sqrt(m));
for (int y = 1; y < k; y++) {
for (int x = y + 1; x < k; x++) {
if (isRelativePrime(x, y) && (x + y) % 2 == 1) {
int a = x * x - y * y;
int b = 2 * x * y;
int c = x * x + y * y;
if (a >= n && b >= n && c <= m) {
ans.add(a < b ? new int[] {a, b, c} : new int[] {b, a, c});
}
}
}
}
if (ans.size() > 0) {
ans.sort((a, b) -> a[0] != b[0] ? a[0] - b[0] : a[1] != b[1] ? a[1] - b[1] : a[2] - b[2]);
for (int[] arr : ans) {
System.out.println(arr[0] + " " + arr[1] + " " + arr[2]);
}
} else {
System.out.println("NA");
}
}
// 判断两个数是否互质,辗转相除
public static boolean isRelativePrime(int x, int y) {
while (y > 0) {
int mod = x % y;
x = y;
y = mod;
}
return x == 1;
}
}
Python算法源码
import math
# 输入获取
n = int(input())
m = int(input())
# 判断两个数是否互质,辗转相除
def isRelativePrime(x, y):
while y > 0:
mod = x % y
x = y
y = mod
return x == 1
# 算法入口
def getResult():
ans = []
k = math.ceil(math.sqrt(m))
for y in range(1, k):
for x in range(y + 1, k):
# 互质勾股数
if isRelativePrime(x, y) and (x + y) % 2 == 1:
a = x * x - y * y
b = 2 * x * y
c = x * x + y * y
if a >= n and b >= n and c <= m:
ans.append([a, b, c] if a < b else [b, a, c])
if len(ans) > 0:
ans.sort()
for lst in ans:
print(" ".join(map(str, lst)))
else:
print("NA")
# 算法调用
getResult()
免责声明:
评论0