题目描述
围棋棋盘由纵横各19条线垂直相交组成,棋盘上一共19 x 19 = 361 个交点,对弈双方一方执白棋,一方执黑棋,落子时只能将棋子置于交点上。
“气”是围棋中很重要的一个概念,某个棋子有几口气,是指其上下左右方向四个相邻的交叉点中,有几个交叉点没有棋子,由此可知:
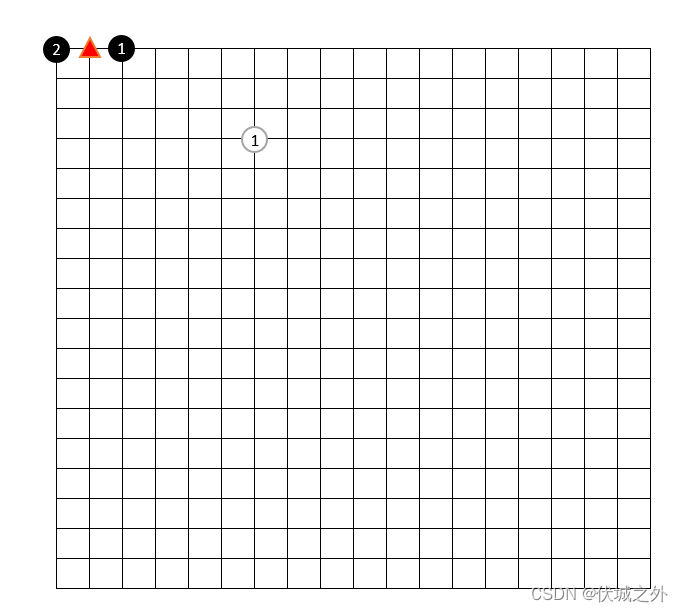
- 在棋盘的边缘上的棋子最多有 3 口气(黑1),在棋盘角点的棋子最多有2口气(黑2),其他情况最多有4口气(白1)
- 所有同色棋子的气之和叫做该色棋子的气,需要注意的是,同色棋子重合的气点,对于该颜色棋子来说,只能计算一次气,比如下图中,黑棋一共4口气,而不是5口气,因为黑1和黑2中间红色三角标出来的气是两个黑棋共有的,对于黑棋整体来说只能算一个气。
- 本题目只计算气,对于眼也按气计算,如果您不清楚“眼”的概念,可忽略,按照前面描述的规则计算即可。
现在,请根据输入的黑棋和白棋得到坐标位置,计算黑棋和白棋一共各有多少气?
输入描述
输入包含两行数据,如:
0 5 8 9 9 10
5 0 9 9 9 8
- 每行数据以空格分隔,数据个数是2的整数倍,每两个数是一组,代表棋子在棋盘上的坐标;
- 坐标的原点在棋盘左上角点,第一个值是行号,范围从0到18;第二个值是列号,范围从0到18。
- 举例说明:第一行数据表示三个坐标(0, 5)、(8, 9)、(9, 10)
- 第一行表示黑棋的坐标,第二行表示白棋的坐标。
- 题目保证输入两行数据,无空行且每行按前文要求是偶数个,每个坐标不会超出棋盘范围。
输出描述
8 7
两个数字以空格分隔,第一个数代表黑棋的气数,第二个数代表白棋的气数。
用例
| 输入 | 0 5 8 9 9 10 5 0 9 9 9 8 |
| 输出 | 8 7 |
| 说明 |
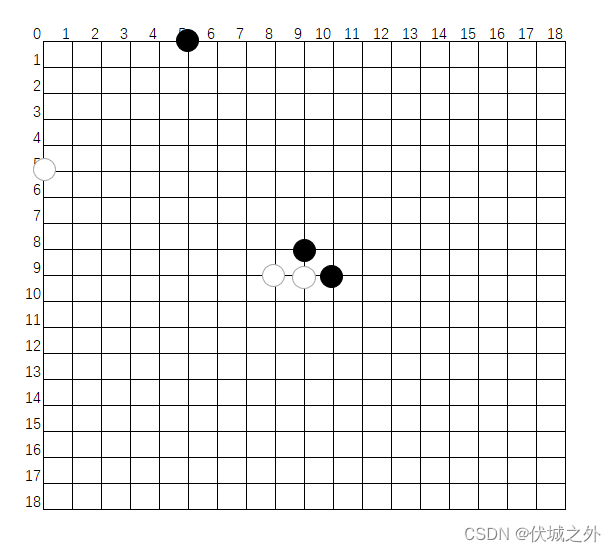
如果将输入数据放到棋盘上
数数黑棋一共8口气,数数白棋一共7口气。 |
题目解析
本题棋盘中“气”的位置有如下特点:
- 该位置没有棋子
- 该位置上下左右存在至少一个棋子(若为黑棋,则当前位置就是黑棋的气,若为白棋,则当前位置就是白棋的气,若既有黑棋,也有白棋,则同时为两个颜色棋的气)
因此,我们只需要遍历19*19的棋盘中每一个位置,检查对应位置是否有棋子,若没有棋子,则检查其上下左右四个位置是否存在黑棋、白棋,若存在则对应颜色的棋子的气数+1,需要注意的是,一个位置只能产生一个气,因此如果该位置的上下左右位置有多个黑棋,也只能为黑棋加一个气,白棋同理。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const black = (await readline()).split(" ").map(Number);
const white = (await readline()).split(" ").map(Number);
// 定义棋盘,没有棋子用0表示
const board = new Array(19).fill(0).map(() => new Array(19).fill(0));
for (let i = 0; i < black.length; i += 2) {
const x = black[i];
const y = black[i + 1];
board[x][y] = 1; // 棋盘中黑棋用1表示
}
for (let i = 0; i < white.length; i += 2) {
const x = white[i];
const y = white[i + 1];
board[x][y] = 2; // 棋盘中白棋用2表示
}
// 黑棋的气数
let black_liberty_count = 0;
// 白棋的气数
let white_liberty_count = 0;
// 上下左右四个方向的偏移量
const offsets = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1],
];
for (let i = 0; i < 19; i++) {
for (let j = 0; j < 19; j++) {
// 如果当前位置没有棋子,则可能是黑棋或白棋的气
if (board[i][j] == 0) {
// 当前位置是否为黑棋的气
let isBlackLiberty = false;
// 当前位置是否白棋的气
let isWhiteLiberty = false;
// 若为黑棋或者白棋的气,则当前位置的上下左右的位置上必有黑棋或白棋
for (let [offsetX, offsetY] of offsets) {
const newI = i + offsetX;
const newJ = j + offsetY;
// 若当前位置的上下左右的位置越界,则不考虑
if (newI < 0 || newI >= 19 || newJ < 0 || newJ >= 19) continue;
// 若当前位置的上下左右的位置存在黑棋,则当前位置为黑棋的气
isBlackLiberty = isBlackLiberty || board[newI][newJ] == 1;
// 若当前位置的上下左右的位置存在白棋,则当前位置为白棋的气
isWhiteLiberty = isWhiteLiberty || board[newI][newJ] == 2;
}
if (isBlackLiberty) black_liberty_count++;
if (isWhiteLiberty) white_liberty_count++;
}
}
}
console.log(`${black_liberty_count} ${white_liberty_count}`);
})();
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] black = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int[] white = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
// 定义棋盘,没有棋子用0表示
int[][] board = new int[19][19];
for (int i = 0; i < black.length; i += 2) {
int x = black[i];
int y = black[i + 1];
board[x][y] = 1; // 棋盘中黑棋用1表示
}
for (int i = 0; i < white.length; i += 2) {
int x = white[i];
int y = white[i + 1];
board[x][y] = 2; // 棋盘中白棋用2表示
}
// 黑棋的气数
int black_liberty_count = 0;
// 白棋的气数
int white_liberty_count = 0;
// 上下左右四个方向的偏移量
int[][] offsets = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (int i = 0; i < 19; i++) {
for (int j = 0; j < 19; j++) {
// 如果当前位置没有棋子,则可能是黑棋或白棋的气
if (board[i][j] == 0) {
// 当前位置是否为黑棋的气
boolean isBlackLiberty = false;
// 当前位置是否白棋的气
boolean isWhiteLiberty = false;
// 若为黑棋或者白棋的气,则当前位置的上下左右的位置上必有黑棋或白棋
for (int[] offset : offsets) {
int newI = i + offset[0];
int newJ = j + offset[1];
// 若当前位置的上下左右的位置越界,则不考虑
if (newI < 0 || newI >= 19 || newJ < 0 || newJ >= 19) continue;
// 若当前位置的上下左右的位置存在黑棋,则当前位置为黑棋的气
isBlackLiberty = isBlackLiberty || (board[newI][newJ] == 1);
// 若当前位置的上下左右的位置存在白棋,则当前位置为白棋的气
isWhiteLiberty = isWhiteLiberty || (board[newI][newJ] == 2);
}
if (isBlackLiberty) black_liberty_count++;
if (isWhiteLiberty) white_liberty_count++;
}
}
}
System.out.println(black_liberty_count + " " + white_liberty_count);
}
}
Python算法源码
# 输入获取
black = list(map(int, input().split()))
white = list(map(int, input().split()))
# 算法入口
def getResult():
# 定义棋盘,没有棋子用0表示
board = [[0] * 19 for _ in range(19)]
for i in range(0, len(black), 2):
x = black[i]
y = black[i + 1]
board[x][y] = 1 # 棋盘中黑棋用1表示
for i in range(0, len(white), 2):
x = white[i]
y = white[i + 1]
board[x][y] = 2 # 棋盘中白棋用2表示
# 黑棋的气数
black_liberty_count = 0
# 白棋的气数
white_liberty_count = 0
# 上下左右四个方向的偏移量
offsets = ((-1, 0), (1, 0), (0, -1), (0, 1))
for i in range(19):
for j in range(19):
# 如果当前位置没有棋子,则可能是黑棋或白棋的气
if board[i][j] == 0:
# 当前位置是否为黑棋的气
isBlackLiberty = False
# 当前位置是否白棋的气
isWhiteLiberty = False
# 若为黑棋或者白棋的气,则当前位置的上下左右的位置上必有黑棋或白棋
for offsetX, offsetY in offsets:
newI = i + offsetX
newJ = j + offsetY
# 若当前位置的上下左右的位置越界,则不考虑
if newI < 0 or newI >= 19 or newJ < 0 or newJ >= 19:
continue
# 若当前位置的上下左右的位置存在黑棋,则当前位置为黑棋的气
isBlackLiberty = isBlackLiberty or (board[newI][newJ] == 1)
# 若当前位置的上下左右的位置存在白棋,则当前位置为白棋的气
isWhiteLiberty = isWhiteLiberty or (board[newI][newJ] == 2)
if isBlackLiberty:
black_liberty_count += 1
if isWhiteLiberty:
white_liberty_count += 1
return f"{black_liberty_count} {white_liberty_count}"
# 算法调用
print(getResult())C算法源码
#include <stdio.h>
#define MAX_SIZE 722
int main() {
int black[MAX_SIZE];
int black_size = 0;
while (scanf("%d", &black[black_size++])) {
if (getchar() != ' ') break;
}
int white[MAX_SIZE];
int white_size = 0;
while (scanf("%d", &white[white_size++])) {
if (getchar() != ' ') break;
}
// 定义棋盘,没有棋子用0表示
int board[19][19] = {0};
for (int i = 0; i < black_size; i += 2) {
int x = black[i];
int y = black[i + 1];
board[x][y] = 1; // 棋盘中黑棋用1表示
}
for (int i = 0; i < white_size; i += 2) {
int x = white[i];
int y = white[i + 1];
board[x][y] = 2; // 棋盘中白棋用2表示
}
// 黑棋的气数
int black_liberty_count = 0;
// 白棋的气数
int white_liberty_count = 0;
// 上下左右四个方向的偏移量
int offsets[4][2] = {{-1, 0},
{1, 0},
{0, -1},
{0, 1}};
for (int i = 0; i < 19; i++) {
for (int j = 0; j < 19; j++) {
// 如果当前位置没有棋子,则可能是黑棋或白棋的气
if (board[i][j] == 0) {
// 当前位置是否为黑棋的气
int isBlackLiberty = 0;
// 当前位置是否白棋的气
int isWhiteLiberty = 0;
// 若为黑棋或者白棋的气,则当前位置的上下左右的位置上必有黑棋或白棋
for (int k = 0; k < 4; k++) {
int newI = i + offsets[k][0];
int newJ = j + offsets[k][1];
// 若当前位置的上下左右的位置越界,则不考虑
if (newI < 0 || newI >= 19 || newJ < 0 || newJ >= 19) continue;
// 若当前位置的上下左右的位置存在黑棋,则当前位置为黑棋的气
isBlackLiberty = isBlackLiberty || (board[newI][newJ] == 1);
// 若当前位置的上下左右的位置存在白棋,则当前位置为白棋的气
isWhiteLiberty = isWhiteLiberty || (board[newI][newJ] == 2);
}
if (isBlackLiberty) black_liberty_count++;
if (isWhiteLiberty) white_liberty_count++;
}
}
}
printf("%d %d", black_liberty_count, white_liberty_count);
return 0;
}免责声明:
1、IT资源小站为非营利性网站,全站所有资料仅供网友个人学习使用,禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享,本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题,请立即告知本站,本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体,但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员,一律视为同意网站规定,本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0