题目描述
给定长度为 n 的无序的数字数组,每个数字代表二叉树的叶子节点的权值,数字数组的值均大于等于1。
请完成一个函数,根据输入的数字数组,生成哈夫曼树,并将哈夫曼树按照中序遍历输出。
为了保证输出的二叉树中序遍历结果统一,增加以下限制:
二叉树节点中,左节点权值小于右节点权值,根节点权值为左右节点权值之和。当左右节点权值相同时,左子树高度小于等于右子树高度。
注意:
所有用例保证有效,并能生成哈夫曼树。
提醒:
哈夫曼树又称为最优二叉树,是一种带权路径长度最短的二叉树。
所谓树的带权路径长度,就是树中所有的叶节点的权值乘上其到根节点的路径长度(若根节点为 0 层,叶节点到根节点的路径长度为叶节点的层数)
输入描述
例如:由叶子节点:5 15 40 30 10,生成的最优二叉树如下图所示,该树的最短带权路径长度为:40 * 1 + 30 * 2 + 5 * 4 + 10 * 4 = 205。
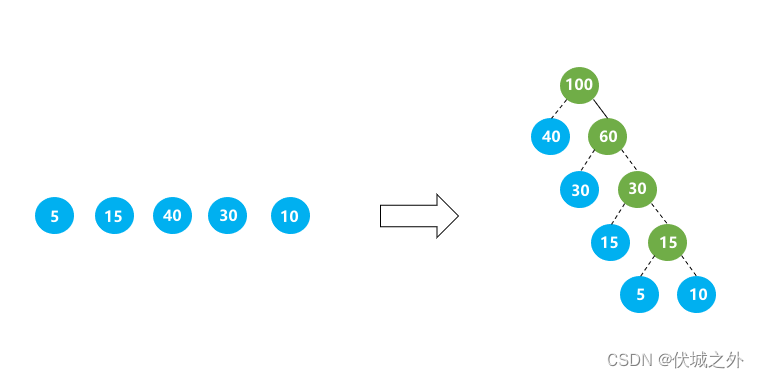
输出描述
输出一个哈夫曼树的中序遍历数组,数值间以空格分隔
用例
| 输入 | 5 5 15 40 30 10 |
| 输出 | 40 100 30 60 15 30 5 15 10 |
| 说明 | 根据输入,生成哈夫曼树,按照中序遍历返回。所有节点中,左节点权值小于等于右节点权值之和。当左右节点权值相同时,左子树高度小于右子树。结果如上图所示。 |
题目解析
本题主要是考察哈夫曼树的构建。
哈夫曼树定义:
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
比如题目用例给出的N个叶子节点的权值分别为:5 15 40 30 10
那么我们可以根据这些叶子节点任意构造一个二叉树,比如下图所示
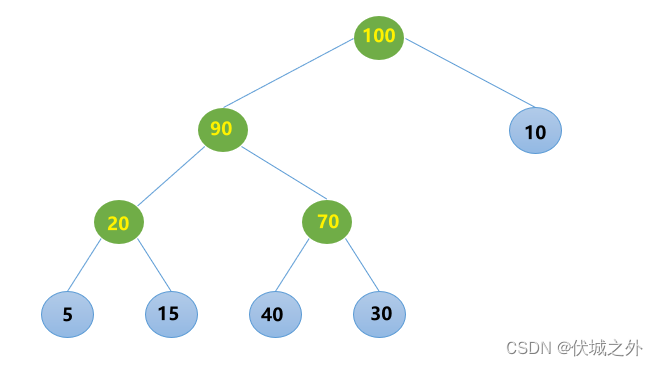
那么这颗二叉树的各个叶子节点的带权路径长度如下:
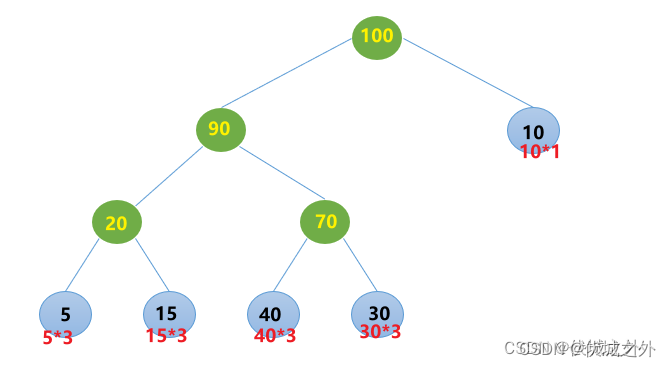
5*3 + 15*3 + 40*3 + 30*3 + 10*1 = 280
因此这颗二叉树的带权路径长度 = 280 要比题目描述中构造的最优二叉树的205大。因此这种二叉树就不是哈夫曼树。
哈夫曼树是根据给定的n个叶子节点构造出的带权路径长度最短的二叉树。
而哈夫曼的构建是有固定思路:
首先,我们从给定的n个叶子节点的权值序列中取出最小的两个,
比如 [5, 15, 40, 30, 10] 中最小的两个是5、10,取出进行合并,则可得如下新节点15(绿色),
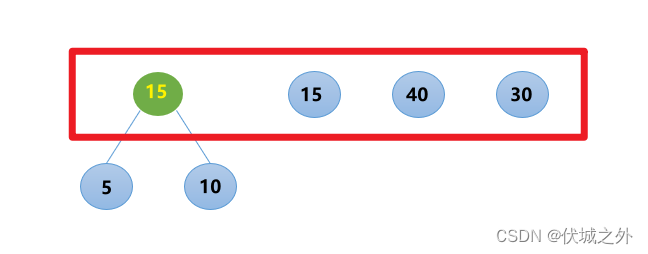
然后将新节点重新加入到权值序列中,得到红框中新序列 [15, 15, 40, 30]
然后再从新序列 [15, 15, 40, 30]中取出最小的两个,进行合并
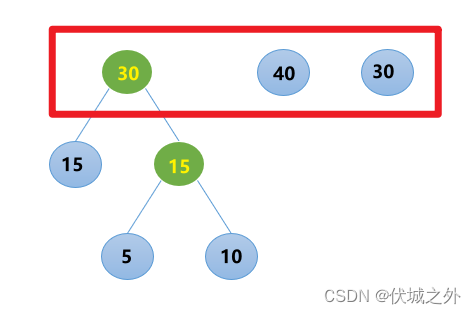
然后再从新序列 [30, 40, 30]中取出最小的两个,进行合并
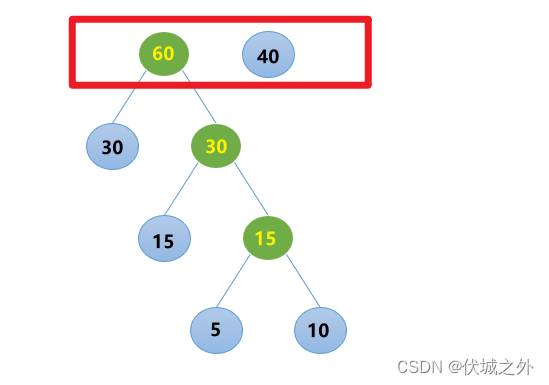
然后再从新序列 [60, 40]中取出最小的两个,进行合并
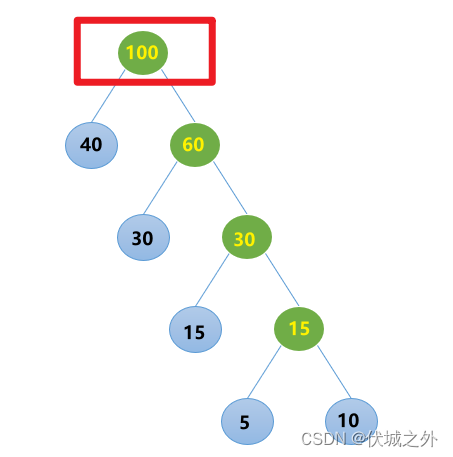
此时序列中只剩下一个节点,即可停止上面逻辑。
按照这种策略构造出来的二叉树的带权路径长度是最短的,即构建出来的是哈夫曼树。
另外,如果初始有N个叶子节点的话,那么构造出来的哈夫曼树的节点总数就有 2 * N – 1 个。
其实,我们通过上图就可以发现规律,蓝色节点是初始N个叶子节点,绿色节点是新建的,而绿色节点的个数 = N – 1。
了解了哈夫曼树的构造原理后,其实本题就很简单了,只需要不停从给定的权值序列中:
- 取出两个最小的权值
- 放回两个最小权值的合并和
直到权值序列中只有一个元素时停止。
而上面取出两个最小、返回合并和后重新排序,这种行为是非常适合使用优先队列(小顶堆)做的。
Java和Python有内置的优先队列实现,而JS和C没有,因此JS和C可以尝试更简单的每次对权值序列进行降序排序,尾部两个就是最小的,放回合并和后再重新降序排序。
下面博客实现中,JS和C手撕优先队列,关于优先队列的原理可以看:
解析中对于优先队列实现剖析。
另外本题说:
为了保证输出的二叉树中序遍历结果统一,增加以下限制:
二叉树节点中,左节点权值小于右节点权值,根节点权值为左右节点权值之和。当左右节点权值相同时,左子树高度小于等于右子树高度。
我的想法是定义哈夫曼树节点,带上一个节点对应子树的高度值,即节点定义如下:
{
left_child: , // 左子节点
right_child: , // 右子节点
weight: , // 当前节点权值
height: // 当前节点对应子树的高度
}
这样优先队列遇到相同权值的节点时,可以继续比较节点子树高度,高度低的优先级更高。
这样取出来的两个节点,第一个取出的肯定作为左子节点,第二个取出的肯定作为右子节点。
但是这种策略无法保证构造出来的哈夫曼树是唯一的,比如下面例子:
4
80 80 20 60
我可以构造出两种哈夫曼树,这两种哈夫曼树的带权路径长度是一样的
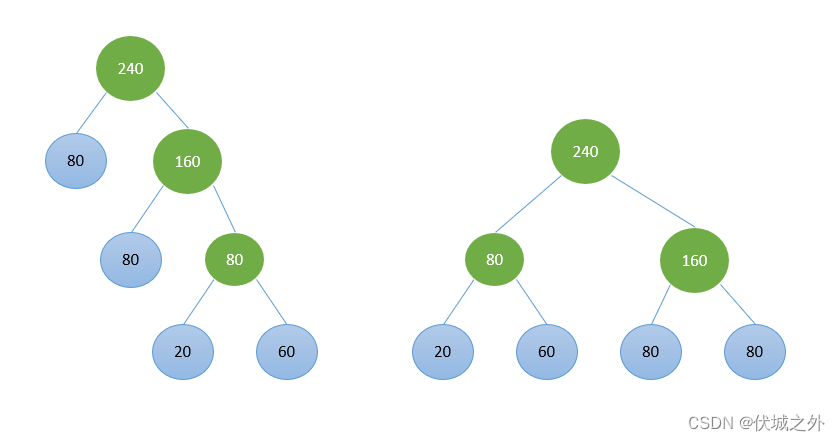
且这两种哈夫曼树都能满足:
二叉树节点中,左节点权值小于右节点权值,根节点权值为左右节点权值之和。当左右节点权值相同时,左子树高度小于等于右子树高度。
之所以会产生两种哈夫曼树,是因为当20、60合并后,新的权值序列中会有3个80
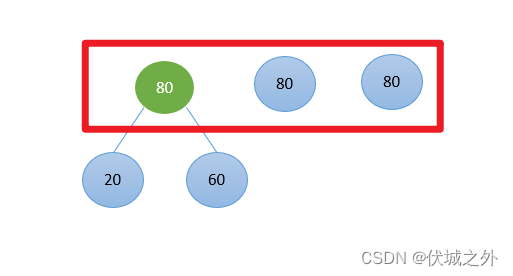
此时,如果一个绿色和一个蓝色优先合并,则得到
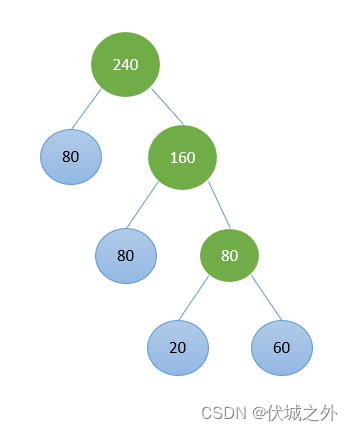
如果两个蓝色优先合并,则得到
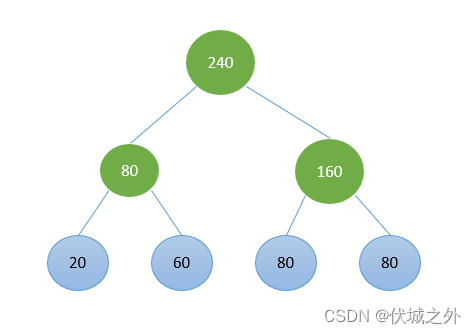
这该咋搞?期望考试用例不会出现这种摸棱两可的情况。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const n = parseInt(await readline());
const weights = (await readline()).split(" ").map(Number);
console.log(getResult(weights));
})();
class Node {
constructor(lc, rc, weight, height) {
this.lc = lc; // 左孩子节点
this.rc = rc; // 右孩子节点
this.weight = weight; // 当前节点的权重
this.height = height; // 当前节点代表子树的高度
}
}
function midOrder(root, seq) {
// 中序遍历,即先遍历二叉树的左子树,再遍历二叉树的根,最后遍历二叉树的右子树
if (root.lc != null) {
midOrder(root.lc, seq);
}
seq.push(root.weight);
if (root.rc != null) {
midOrder(root.rc, seq);
}
}
function getResult(weights) {
// 将哈夫曼树节点进行排序,方便后面筛选出权值最小的两个节点
const pq = new PriorityQueue(
(a, b) => (a.weight != b.weight ? a.weight - b.weight : a.height - b.height) // 题目说:当左右节点权值相同时,左子树高度小于等于右子树高度。因此当节点权重相同时,再按照节点子树高度升序
);
// 创建n个哈夫曼树节点,并加入优先队列
for (let w of weights) {
pq.offer(new Node(null, null, w, 0));
}
// 初始n个节点经过多轮合并,只剩一个节点时,那么该节点就是哈夫曼树的根节点,因此当优先队列中只剩一个节点时即可停止合并
while (pq.size() > 1) {
// 取出优先队列中前两个权值最小的节点,由于优先队列已按照 [节点权重,节点子树高度] 升序优先级,因此先出来的肯定是权重小,或者高度小的节点,即作为新节点的左子树
const lc = pq.poll();
const rc = pq.poll();
// 将lc和rc合并,合并后新节点fa的权重,是两个子节点权重之和,fa子树高度 = rc子树高度+1; PS:rc的高度>=lc的高度
const fa_weight = lc.weight + rc.weight;
const fa_height = rc.height + 1;
// 将合并后的新节点加入优先队列
pq.offer(new Node(lc, rc, fa_weight, fa_height));
}
// 最后优先队列中必然只剩一个节点,即哈夫曼树的根节点,此时对此根节点(哈夫曼树)进行中序遍历
const root = pq.poll();
const seq = [];
midOrder(root, seq);
return seq.join(" ");
}
// 基于堆实现优先队列
class PriorityQueue {
constructor(cpr) {
this.queue = [];
this.cpr = cpr;
}
swap(a, b) {
const tmp = this.queue[a];
this.queue[a] = this.queue[b];
this.queue[b] = tmp;
}
// 上浮
swim() {
let c = this.queue.length - 1;
while (c >= 1) {
const f = Math.floor((c - 1) / 2);
if (this.cpr(this.queue[c], this.queue[f]) < 0) {
this.swap(c, f);
c = f;
} else {
break;
}
}
}
// 入队
offer(val) {
this.queue.push(val);
this.swim();
}
// 下沉
sink() {
let f = 0;
while (true) {
let c1 = 2 * f + 1;
let c2 = c1 + 1;
let c;
let val1 = this.queue[c1];
let val2 = this.queue[c2];
if (val1 != undefined && val2 != undefined) {
c = this.cpr(val1, val2) < 0 ? c1 : c2;
} else if (val1 != undefined) {
c = c1;
} else if (val2 != undefined) {
c = c2;
} else {
break;
}
if (this.cpr(this.queue[c], this.queue[f]) < 0) {
this.swap(c, f);
f = c;
} else {
break;
}
}
}
// 出队
poll() {
this.swap(0, this.queue.length - 1);
const res = this.queue.pop();
this.sink();
return res;
}
peek() {
return this.queue[0];
}
size() {
return this.queue.length;
}
}
Java算法源码
import java.util.PriorityQueue;
import java.util.Scanner;
import java.util.StringJoiner;
public class Main {
// 哈夫曼树节点
static class Node {
Node lchild; // 左孩子节点
Node rchild; // 右孩子节点
int weight; // 当前节点的权重
int height; // 当前节点代表子树的高度
public Node(Node lc, Node rc, int weight, int height) {
this.lchild = lc;
this.rchild = rc;
this.weight = weight;
this.height = height;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
// 将哈夫曼树节点进行排序,方便后面筛选出权值最小的两个节点
PriorityQueue<Node> pq =
new PriorityQueue<>(
(a, b) ->
a.weight != b.weight
? a.weight - b.weight
: a.height - b.height); // 题目说:当左右节点权值相同时,左子树高度小于等于右子树高度。因此当节点权重相同时,再按照节点子树高度升序
for (int i = 0; i < n; i++) {
// 创建n个哈夫曼树节点
int w = sc.nextInt();
Node node = new Node(null, null, w, 0);
// 加入优先队列
pq.offer(node);
}
// 初始n个节点经过多轮合并,只剩一个节点时,那么该节点就是哈夫曼树的根节点,因此当优先队列中只剩一个节点时即可停止合并
while (pq.size() > 1) {
// 取出优先队列中前两个权值最小的节点,由于优先队列已按照 [节点权重,节点子树高度] 升序优先级,因此先出来的肯定是权重小,或者高度小的节点,即作为新节点的左子树
Node lc = pq.poll();
Node rc = pq.poll();
// 将lc和rc合并,合并后新节点fa的权重,是两个子节点权重之和,fa子树高度 = rc子树高度+1; PS:rc的高度>=lc的高度
int fa_weight = lc.weight + rc.weight;
int fa_height = rc.height + 1;
// 将合并后的新节点加入优先队列
Node fa = new Node(lc, rc, fa_weight, fa_height);
pq.offer(fa);
}
// 最后优先队列中必然只剩一个节点,即哈夫曼树的根节点,此时对此根节点(哈夫曼树)进行中序遍历
Node root = pq.poll();
StringJoiner sj = new StringJoiner(" ");
midOrder(root, sj);
System.out.println(sj);
}
public static void midOrder(Node root, StringJoiner sj) {
// 中序遍历,即先遍历二叉树的左子树,再遍历二叉树的根,最后遍历二叉树的右子树
if (root.lchild != null) {
midOrder(root.lchild, sj);
}
sj.add(root.weight + "");
if (root.rchild != null) {
midOrder(root.rchild, sj);
}
}
}
Python算法源码
import heapq
class Node:
def __init__(self, lc, rc, weight, height):
self.lc = lc # 左孩子节点
self.rc = rc # 右孩子节点
self.weight = weight # 当前节点的权重
self.height = height # 当前节点代表子树的高度
def __gt__(self, other):
# 优先级比较时,权重小的优先级更高,权重相同时,高度小的优先级更高
if self.weight != other.weight:
return self.weight > other.weight
else:
return self.height > other.height
# 输入获取
n = int(input())
weights = list(map(int, input().split()))
# 二叉树中序遍历
def midOrder(root, seq):
# 中序遍历,即先遍历二叉树的左子树,再遍历二叉树的根,最后遍历二叉树的右子树
if root.lc is not None:
midOrder(root.lc, seq)
seq.append(root.weight)
if root.rc is not None:
midOrder(root.rc, seq)
# 算法入口
def getResult():
pq = []
# 创建n个哈夫曼树节点,并加入优先队列
for w in weights:
heapq.heappush(pq, Node(None, None, w, 0))
# 初始n个节点经过多轮合并,只剩一个节点时,那么该节点就是哈夫曼树的根节点,因此当优先队列中只剩一个节点时即可停止合并
while len(pq) > 1:
# 取出优先队列中前两个权值最小的节点,由于优先队列已按照 [节点权重,节点子树高度] 升序优先级,因此先出来的肯定是权重小,或者高度小的节点,即作为新节点的左子树
lc = heapq.heappop(pq)
rc = heapq.heappop(pq)
# 将lc和rc合并,合并后新节点fa的权重,是两个子节点权重之和,fa子树高度 = rc子树高度+1; PS:rc的高度>=lc的高度
fa_weight = lc.weight + rc.weight
fa_height = rc.height + 1
# 将合并后的新节点加入优先队列
heapq.heappush(pq, Node(lc, rc, fa_weight, fa_height))
# 最后优先队列中必然只剩一个节点,即哈夫曼树的根节点,此时对此根节点(哈夫曼树)进行中序遍历
root = heapq.heappop(pq)
seq = []
midOrder(root, seq)
return " ".join(map(str, seq))
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <stdlib.h>
// 哈夫曼树节点
typedef struct Node {
struct Node *lc; // 左孩子节点
struct Node *rc; // 右孩子节点
int weight; // 当前节点的权重
int height; // 当前节点代表子树的高度
} Node;
Node *new_Node(Node *lc, Node *rc, int weight, int height) {
Node *node = (Node *) malloc(sizeof(Node));
node->lc = lc;
node->rc = rc;
node->weight = weight;
node->height = height;
return node;
}
/* 优先队列实现 */
typedef Node *E;
typedef struct PriorityQueue {
E *arr;
int size;
int (*cmp)(E, E);
} PQ;
PQ *new_PQ(int capacity, int (*cmp)(E, E)) {
PQ *pq = (PQ *) malloc(sizeof(PQ));
pq->arr = (E *) malloc(sizeof(int) * capacity);
pq->size = 0;
pq->cmp = cmp;
return pq;
}
void swap_PQ(PQ *pq, int a, int b) {
E tmp = pq->arr[a];
pq->arr[a] = pq->arr[b];
pq->arr[b] = tmp;
}
// 上浮
void swim_PQ(PQ *pq) {
int c = pq->size - 1;
while (c >= 1) {
int f = (c - 1) / 2;
if (pq->cmp(pq->arr[c], pq->arr[f]) < 0) {
swap_PQ(pq, c, f);
c = f;
} else {
break;
}
}
}
// 入队
void offer_PQ(PQ *pq, E val) {
pq->arr[pq->size++] = val;
swim_PQ(pq);
}
// 下沉
void sink_PQ(PQ *pq) {
int f = 0;
while (1) {
int c1 = 2 * f + 1;
int c2 = c1 + 1;
int c;
if (pq->size > c1 && pq->size > c2) {
if (pq->cmp(pq->arr[c1], pq->arr[c2]) < 0) {
c = c1;
} else {
c = c2;
}
} else if (pq->size > c1 && pq->size <= c2) {
c = c1;
} else if (pq->size <= c1 && pq->size > c2) {
c = c2;
} else {
break;
}
if (pq->cmp(pq->arr[c], pq->arr[f]) < 0) {
swap_PQ(pq, c, f);
f = c;
} else {
break;
}
}
}
// 出队
E poll_PQ(PQ *pq) {
swap_PQ(pq, 0, pq->size - 1);
E res = pq->arr[--pq->size];
sink_PQ(pq);
return res;
}
int cmp_PQ(Node *a, Node *b) {
if (a->weight != b->weight) {
return a->weight - b->weight;
} else {
return a->height - b->height;
}
}
void midOrder(Node *root) {
// 中序遍历,即先遍历二叉树的左子树,再遍历二叉树的根,最后遍历二叉树的右子树
if (root->lc != NULL) {
midOrder(root->lc);
}
printf("%d ", root->weight);
if (root->rc != NULL) {
midOrder(root->rc);
}
}
int main() {
int n;
scanf("%d", &n);
// n个叶子节点的哈夫曼树,总节点数为 2 * n - 1,因此这里pq只需要开2*n-1的空间即可
// 将哈夫曼树节点进行排序,方便后面筛选出权值最小的两个节点
PQ *pq = new_PQ(2 * n - 1, cmp_PQ);
// 创建n个哈夫曼树节点加入优先队列
for (int i = 0; i < n; i++) {
int w;
scanf("%d", &w);
Node *node = new_Node(NULL, NULL, w, 0);
offer_PQ(pq, node);
}
// 初始n个节点经过多轮合并,只剩一个节点时,那么该节点就是哈夫曼树的根节点,因此当优先队列中只剩一个节点时即可停止合并
while (pq->size > 1) {
// 取出优先队列中前两个权值最小的节点,由于优先队列已按照 [节点权重,节点子树高度] 升序优先级,因此先出来的肯定是权重小,或者高度小的节点,即作为新节点的左子树
Node *lc = poll_PQ(pq);
Node *rc = poll_PQ(pq);
// 将lc和rc合并,合并后新节点fa的权重,是两个子节点权重之和,fa子树高度 = rc子树高度+1; PS:rc的高度>=lc的高度
int fa_weight = lc->weight + rc->weight;
int fa_height = rc->height + 1;
// 将合并后的新节点加入优先队列
Node *fa = new_Node(lc, rc, fa_weight, fa_height);
offer_PQ(pq, fa);
}
// 最后优先队列中必然只剩一个节点,即哈夫曼树的根节点,此时对此根节点(哈夫曼树)进行中序遍历
midOrder(poll_PQ(pq));
return 0;
}免责声明:
评论0