当前位置： 2024华为OD机试题库 (C卷,200分)- 两个字符串间的最短路径问题（Java & JS & Python & C）

(C卷,200分)- 两个字符串间的最短路径问题（Java & JS & Python & C）

2024-05-07 27

题目描述

给定两个字符串，分别为字符串 A 与字符串 B。

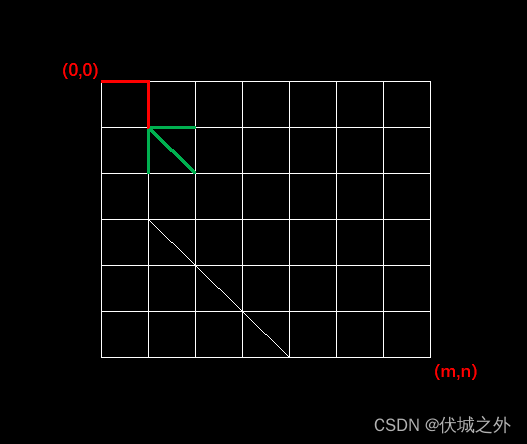
例如 A字符串为 "ABCABBA"，B字符串为 "CBABAC" 可以得到下图 m * n 的二维数组，定义原点为(0,0)，终点为(m,n)，水平与垂直的每一条边距离为1，映射成坐标系如下图。

从原点 (0,0) 到 (0,A) 为水平边，距离为1，从 (0,A) 到 (A,C) 为垂直边，距离为1；

假设两个字符串同一位置的两个字符相同，则可以作一个斜边，如 (A,C) 到 (B,B) 最短距离为斜边，距离同样为1。

作出所有的斜边如下图，(0,0) 到 (B,B) 的距离为：1 个水平边 + 1 个垂直边 + 1 个斜边 = 3。

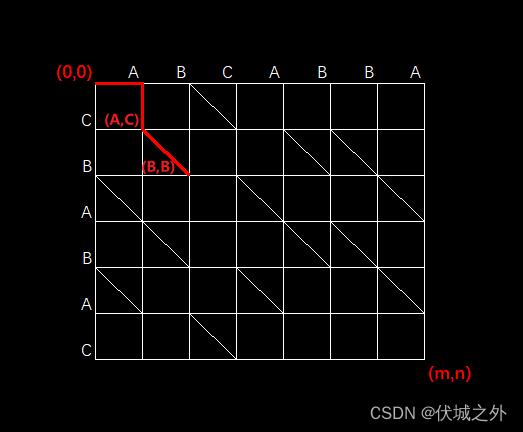
根据定义可知，原点到终点的最短距离路径如下图红线标记，最短距离为9：

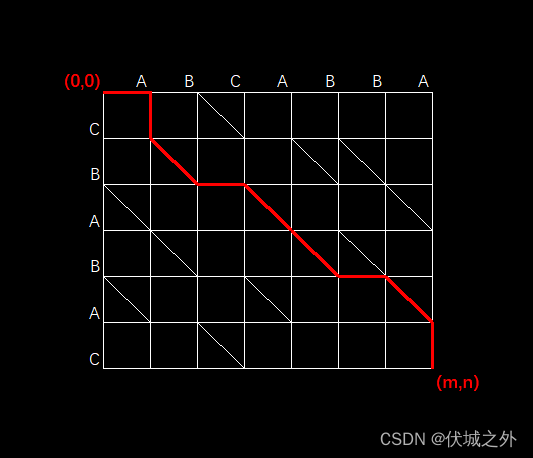
输入描述

空格分割的两个字符串 A 与字符串 B

  • 字符串不为"空串"
  • 字符格式满足正则规则：[A-Z]
  • 字符串长度 < 10000

输出描述

原点到终点的最短距离

用例

输入 ABC ABC
输出 3
说明 无
输入 ABCABBA CBABAC
输出 9
说明 无

题目解析

本题可以通过动态规划来求解：

我们假设dp[i][j]表示(0,0)到(i,j)的最短距离，那么这个最短距离只可能来自三个方向：

  • dp[i-1][j]，当前点的上方点
  • dp[i][j-1]，当前点的左边点
  • dp[i-1][j-1]，当前点的左上方点

而存在推导式如下：

dp[i][j] = min(dp[i-1][j]，dp[i][j-1]，dp[i-1][j-1]) + 1

另外需要注意的是，上面推导式dp[i-1][j-1]参与比较是有前提条件的，即如果(i-1, j-1)点和(i,j)点之间存在斜线相连时，才能将dp[i-1][j-1]带入上面推导式，否则不能带入。

并且上面推导式还可以优化，如果当前点可以向三个方向扩散：

  • 向右
  • 向下
  • 向右下

那么向右和向下是否有必要扩散呢？比如下图

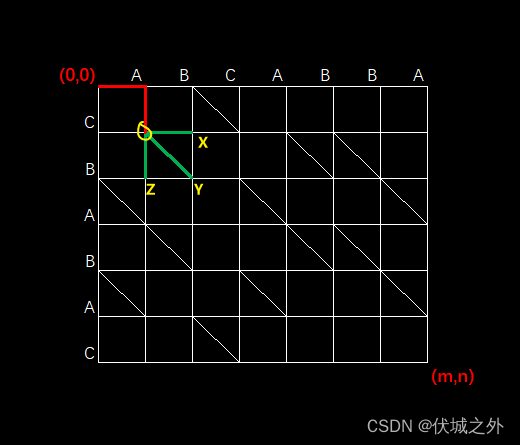
从(1,1)处可以向三个方向扩散，此时可以看出扩散后的三个新位置X,Y,Z，其中Y要比X,Z更靠近右下角点。

那么有没有可能存在一种路径，比如Z点沿着这条路径到达右下角点更快呢？我们改造一下上面图示：

假设存在下面路径，可以让Z点快速到达右下角点，此时我们可以发现，其实Y点也可以凭借该路径以一样的路径长度到达

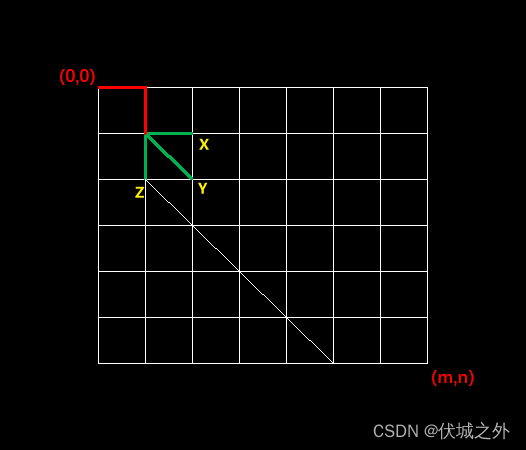
因此，如果如果存在一条路径可以让Z快速到达右下角点，那么Y一定也可以借用到这条路径，以一样的距离到达右下角点。再给个图示例子：

因此，优化思路是，如果当前点可以向三个方向扩散，那么此时可以只扩散：向右下斜边方向。

即推导式可以变为：

  • 如果（i-1, j-1）和（i,j）之间存在斜线相连，则dp[i][j] = dp[i-1][j-1] + 1
  • 否则：dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + 1

本题数量级较大，因此如果构造一个m行n列的dp矩阵，那么会超出内存限制。

优化思路是使用压缩数组，我们可以先看下下面的纯动态规划解法，可以发现

初始化好dp数组的第一行，第一列后，我们通过两个for循环开始完成dp数组其他位置元素的求解，但是本质上还是逐行求解的。

因此，我们完全只需要保留两行：preRow用于记录前一行的dp元素值，curRow用于保存当前行的dp元素值。

curRow仅需要根据preRow即可完成所有元素求解。（PS：curRow的第一列元素值取值即为所在行号）

这样我们就避免了dp数组记录一些过期数据。

JS算法源码

动态规划解法（下面解法会超出内存限制，但是好理解，是后面一种压缩数组解法的基础）
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

void (async function () {
  const [A, B] = (await readline()).split(" ");

  const m = B.length;
  const n = A.length;

  // dp[i][j] 记录的是(0,0)到达点(i, j)的最短路径
  const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));

  // (0,0)到达矩阵第一行上的各点的最短路径，即为(0,0) -> (0,j) 的直线路径
  for (let j = 0; j <= n; j++) {
    dp[0][j] = j;
  }

  // (0,0)到达矩阵第一列上的各点的最短路径，即为(0,0) -> (i,0) 的直线路径
  for (let i = 0; i <= m; i++) {
    dp[i][0] = i;
  }

  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      if (A[j - 1] == B[i - 1]) {
        // 如果可以走斜线，则选走斜线的点
        dp[i][j] = dp[i - 1][j - 1] + 1;
      } else {
        // 如果不能走斜线，则从当前点的上方点、左方点中选择一个较小值
        dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
      }
    }
  }

  console.log(dp[m][n]);
})();
动态规划+压缩数组（可以对比上面代码进行理解）
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

void (async function () {
  const [A, B] = (await readline()).split(" ");

  const m = B.length;
  const n = A.length;

  // 初始时preRow记录第一行上各点到(0,0)点的最短距离，即为(0,0) -> (0,j) 的直线路径
  const preRow = new Array(n + 1).fill(0).map((_, j) => j);

  // 初始时curRow记录第二行上各点到(0,0)点的最短距离
  const curRow = new Array(n + 1);

  for (let i = 1; i <= m; i++) {
    // curRow[0]是指 (i, 0)点 到 (0,0)点 的最短距离，即为(0,0) -> (i, 0) 的直线路径
    curRow[0] = i;

    for (let j = 1; j <= n; j++) {
      if (A[j - 1] == B[i - 1]) {
        // 如果可以走斜线，则选走斜线的点
        curRow[j] = preRow[j - 1] + 1;
      } else {
        // 如果不能走斜线，则从当前点的上方点、左方点中选择一个较小值
        curRow[j] = Math.min(preRow[j], curRow[j - 1]) + 1;
      }
    }

    // 压缩
    for (let j = 0; j <= n; j++) preRow[j] = curRow[j];
  }

  console.log(curRow[n]);
})();

Java算法源码

动态规划解法（下面解法会超出内存限制，但是好理解，是后面一种压缩数组解法的基础）
import java.util.Scanner;

public class Main {
  static String A;
  static String B;
  static int m;
  static int n;

  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);

    A = sc.next();
    B = sc.next();

    m = B.length();
    n = A.length();

    System.out.println(getResult());
  }

  public static int getResult() {
    // dp[i][j] 记录的是(0,0)到达点(i, j)的最短路径
    int[][] dp = new int[m + 1][n + 1];

    // (0,0)到达矩阵第一行上的各点的最短路径，即为(0,0) -> (0,j) 的直线路径
    for (int j = 0; j <= n; j++) {
      dp[0][j] = j;
    }

    // (0,0)到达矩阵第一列上的各点的最短路径，即为(0,0) -> (i,0) 的直线路径
    for (int i = 0; i <= m; i++) {
      dp[i][0] = i;
    }

    for (int i = 1; i <= m; i++) {
      for (int j = 1; j <= n; j++) {
        if (A.charAt(j - 1) == B.charAt(i - 1)) {
          // 如果可以走斜线，则选走斜线的点
          dp[i][j] = dp[i - 1][j - 1] + 1;
        } else {
          // 如果不能走斜线，则从当前点的上方点、左方点中选择一个较小值
          dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
        }
      }
    }

    return dp[m][n];
  }
}
动态规划+压缩数组（可以对比上面代码进行理解）
import java.util.Scanner;

public class Main {
  static String A;
  static String B;
  static int m;
  static int n;

  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);

    A = sc.next();
    B = sc.next();

    m = B.length();
    n = A.length();

    System.out.println(getResult());
  }

  public static int getResult() {
    // 初始时preRow记录第一行上各点到(0,0)点的最短距离，即为(0,0) -> (0,j) 的直线路径
    int[] preRow = new int[n + 1];
    for (int j = 0; j <= n; j++) {
      preRow[j] = j;
    }

    // 初始时curRow记录第二行上各点到(0,0)点的最短距离
    int[] curRow = new int[n + 1];

    for (int i = 1; i <= m; i++) {
      // curRow[0]是指 (i, 0)点 到 (0,0)点 的最短距离，即为(0,0) -> (i, 0) 的直线路径
      curRow[0] = i;

      for (int j = 1; j <= n; j++) {
        if (A.charAt(j - 1) == B.charAt(i - 1)) {
          // 如果可以走斜线，则选走斜线的点
          curRow[j] = preRow[j - 1] + 1;
        } else {
          // 如果不能走斜线，则从当前点的上方点、左方点中选择一个较小值
          curRow[j] = Math.min(preRow[j], curRow[j - 1]) + 1;
        }
      }

      // 压缩
      System.arraycopy(curRow, 0, preRow, 0, n + 1);
    }

    return curRow[n];
  }
}

Python算法源码

动态规划解法（下面解法会超出内存限制，但是好理解，是后面一种压缩数组解法的基础）
# 输入获取
A, B = input().split()
m, n = len(B), len(A)


# 算法入口
def getResult():
    # dp[i][j] 记录的是(0,0)到达点(i, j)的最短路径
    dp = [[0] * (n + 1) for _ in range(m + 1)]

    # (0,0)到达矩阵第一行上的各点的最短路径，即为(0,0) -> (0,j) 的直线路径
    for j in range(n + 1):
        dp[0][j] = j

    # (0,0)到达矩阵第一列上的各点的最短路径，即为(0,0) -> (i,0) 的直线路径
    for i in range(m + 1):
        dp[i][0] = i

    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if A[j - 1] == B[i - 1]:
                # 如果可以走斜线，则选走斜线的点
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                # 如果不能走斜线，则从当前点的上方点、左方点中选择一个较小值
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1

    return dp[m][n]


# 算法调用
print(getResult())
动态规划+压缩数组（可以对比上面代码进行理解）
# 输入获取
A, B = input().split()
m, n = len(B), len(A)


# 算法入口
def getResult():
    # 初始时preRow记录第一行上各点到(0,0)点的最短距离，即为(0,0) -> (0,j) 的直线路径
    preRow = [i for i in range(n + 1)]

    # 初始时curRow记录第二行上各点到(0,0)点的最短距离
    curRow = [0] * (n + 1)

    for i in range(1, m + 1):
        # curRow[0]是指 (i, 0)点 到 (0,0)点 的最短距离，即为(0,0) -> (i, 0) 的直线路径
        curRow[0] = i

        for j in range(1, n + 1):
            if A[j - 1] == B[i - 1]:
                # 如果可以走斜线，则选走斜线的点
                curRow[j] = preRow[j - 1] + 1
            else:
                # 如果不能走斜线，则从当前点的上方点、左方点中选择一个较小值
                curRow[j] = min(preRow[j], curRow[j - 1]) + 1

        # 压缩
        for j in range(n + 1):
            preRow[j] = curRow[j]

    return curRow[n]


# 算法调用
print(getResult())

C算法源码

动态规划解法（下面解法会超出内存限制，但是好理解，是后面一种压缩数组解法的基础）
#include <stdio.h>
#include <string.h>
#include <math.h>

int main() {
    char A[10000];
    scanf("%s", A);

    char B[10000];
    scanf("%s", B);

    int m = (int) strlen(B);
    int n = (int) strlen(A);

    // dp[i][j] 记录的是(0,0)到达点(i, j)的最短路径
    int dp[m + 1][n + 1];

    // (0,0)到达矩阵第一行上的各点的最短路径，即为(0,0) -> (0,j) 的直线路径
    for (int j = 0; j <= n; j++) {
        dp[0][j] = j;
    }

    // (0,0)到达矩阵第一列上的各点的最短路径，即为(0,0) -> (i,0) 的直线路径
    for (int i = 0; i <= m; i++) {
        dp[i][0] = i;
    }

    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (A[j - 1] == B[i - 1]) {
                // 如果可以走斜线，则选走斜线的点
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                // 如果不能走斜线，则从当前点的上方点、左方点中选择一个较小值
                dp[i][j] = (int) fmin(dp[i - 1][j], dp[i][j - 1]) + 1;
            }
        }
    }

    printf("%d", dp[m][n]);

    return 0;
}
动态规划+压缩数组（可以对比上面代码进行理解）
#include <stdio.h>
#include <string.h>
#include <math.h>

int main() {
    char A[10000];
    scanf("%s", A);

    char B[10000];
    scanf("%s", B);

    int m = (int) strlen(B);
    int n = (int) strlen(A);

    // 初始时preRow记录第一行上各点到(0,0)点的最短距离，即为(0,0) -> (0,j) 的直线路径
    int preRow[n + 1];
    for (int j = 0; j <= n; j++) {
        preRow[j] = j;
    }

    // 初始时curRow记录第二行上各点到(0,0)点的最短距离
    int curRow[n + 1];

    for (int i = 1; i <= m; i++) {
        // curRow[0]是指 (i, 0)点 到 (0,0)点 的最短距离，即为(0,0) -> (i, 0) 的直线路径
        curRow[0] = i;

        for (int j = 1; j <= n; j++) {
            if (A[j - 1] == B[i - 1]) {
                // 如果可以走斜线，则选走斜线的点
                curRow[j] = preRow[j - 1] + 1;
            } else {
                // 如果不能走斜线，则从当前点的上方点、左方点中选择一个较小值
                curRow[j] = (int) fmin(preRow[j], curRow[j - 1]) + 1;
            }
        }

        // 压缩
        for (int j = 0; j <= n; j++) preRow[j] = curRow[j];
    }

    printf("%d", curRow[n]);

    return 0;
}

免责声明：

1、IT资源小站为非营利性网站，全站所有资料仅供网友个人学习使用，禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享，本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题，请立即告知本站，本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体，但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员，一律视为同意网站规定，本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文

0

评论0

取消

首页 发现 VIP 我的

站点公告

没有账号？注册  忘记密码？