题目描述
有一棵二叉树,每个节点由一个大写字母标识(最多26个节点)。
现有两组字母,分别表示后序遍历(左孩子->右孩子->父节点)和中序遍历(左孩子->父节点->右孩子)的结果,请你输出层序遍历的结果。
输入描述
每个输入文件一行,第一个字符串表示后序遍历结果,第二个字符串表示中序遍历结果。(每串只包含大写字母)
中间用单空格分隔。
输出描述
输出仅一行,表示层序遍历的结果,结尾换行。
用例
| 输入 | CBEFDA CBAEDF |
| 输出 | ABDCEF |
| 说明 |
二叉树为: A |
题目解析
二叉树的三种遍历方式:
- 前(根)序遍历:根左右
- 中(根)序遍历:左根右
- 后(根)序遍历:左右根
可以发现,其实前、中、后指的是根的位置,而左右的顺序是不变的,即总是先左后右。
比如,下面是一个最简单的二叉树结构
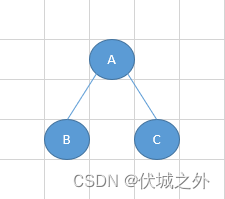
其前序遍历结果为:ABC,中序遍历结果为BAC,后序遍历结果为BCA。
而层序遍历,指的是,从树的顶层开始向下,每层中按照从左向右的顺序遍历节点,因此上图层序遍历结果为ABC。
可能有人会将层序遍历和前序遍历混淆,但是二者是不同的,比如:
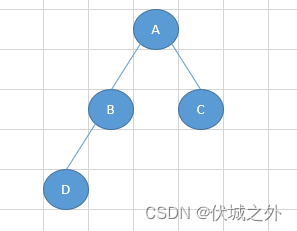
前序遍历结果为:ABDC
层序遍历结果为:ABCD
有了以上关于二叉树遍历的知识后,我们就可以进行用例分析了,用例输入提供了一个二叉树的
后序遍历CBEFDA,以及中序遍历CBAEDF的结果。
首先,我们可以根据后序遍历,快速找到树根,即CBEFDA中的A,因为根据左右根遍历顺序,最后一个遍历元素肯定是这颗树的根节点。
而找到根节点A后,我们又可以在中序遍历的左根右遍历顺序,找到A根的左、右子树,即中序遍历中A节点的左边就是A根的左子树,右边就是A根的右子树。
而找到左右子树后,我们可以根据后序遍历,再分别找到左、右子树的根,然后再根据中序遍历结果,再找出左子树根的左右子树,以及右子树的左右子树。
过程如下图所示:
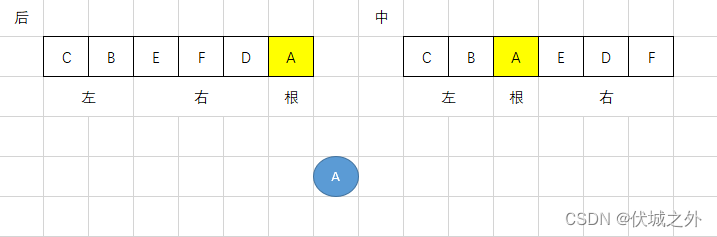
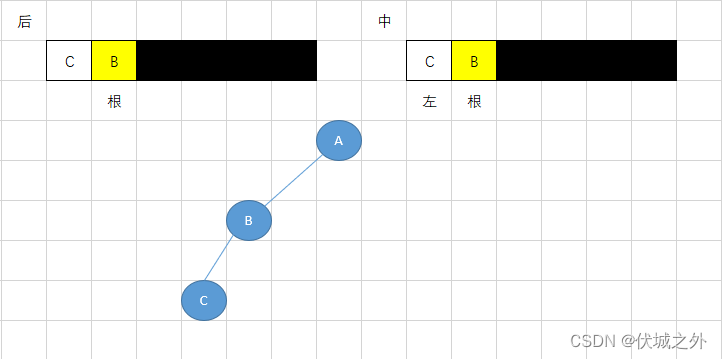
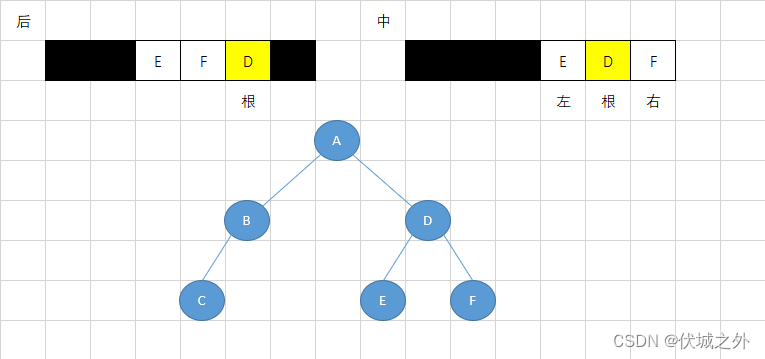
当我们找到的根的左右子树只有1个节点,或没有节点时,则可以停止递归。
当递归完成后,就还原出了一颗树,接下来根据层序遍历规则,即可以得到结果:ABDCEF。
本题解题,貌似需要深度优先搜索DFS来生成树结构,其实不然,我们完全可以改变策略,使用广度优先搜索BFS,来实现层序遍历效果,避免构造树结构,进行二次搜索。
BFS实现层序遍历的逻辑如下:
首先,根据后序遍历结果,找到根A,然后根据中序遍历结果找到根A的左、右子树。
然后,我们就得到了根A左、右子树各自的长度
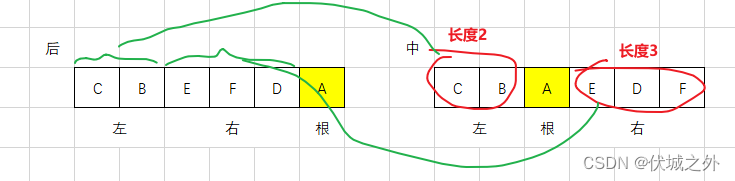
根据左右子树的长度,我们就可以从后序遍历结果中,截取出左、右子树,然后又可以得到左、右子树各自的根(即最后一个元素)。
我们,每次优先遍历子树的根,然后再遍历子树的左右子树。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const [post, mid] = line.split(" ");
console.log(getResult(post, mid));
});
function getResult(post, mid) {
// 广度优先搜索的执行队列,先加入左子树,再加入右子树
const queue = [];
// 层序遍历出来的元素存放在ans中
const ans = [];
devideLR(post, mid, queue, ans);
while (queue.length) {
const [post, mid] = queue.shift();
devideLR(post, mid, queue, ans);
}
return ans.join("");
}
/**
* 本方法用于从后序遍历、中序遍历序列中分离出:根,以及其左、右子树的后序、中序遍历序列
* @param {*} post 后序遍历结果
* @param {*} mid 中序遍历结果
* @param {*} queue BFS的执行队列
* @param {*} ans 题解
*/
function devideLR(post, mid, queue, ans) {
// 后序遍历的最后一个元素就是根
let rootEle = post.at(-1);
// 将根加入题解
ans.push(rootEle);
// 在中序遍历中找到根的位置rootIdx,那么该位置左边就是左子树,右边就是右子树
let rootIdx = mid.indexOf(rootEle);
// 左子树长度,左子树是中序遍历的0~rootIdx-1范围,长度为rootIdx
let leftLen = rootIdx;
// 如果存在左子树,即左子树长度大于0
if (leftLen > 0) {
// 则从后序遍历中,截取出左子树的后序遍历
let leftPost = post.slice(0, leftLen);
// 从中序遍历中,截取出左子树的中序遍历
let leftMid = mid.slice(0, rootIdx);
// 将左子树的后、中遍历序列加入执行队列
queue.push([leftPost, leftMid]);
}
// 如果存在右子树,即右子树长度大于0
if (post.length - 1 - leftLen > 0) {
// 则从后序遍历中,截取出右子树的后序遍历
let rightPost = post.slice(leftLen, post.length - 1);
// 从中序遍历中,截取出右子树的中序遍历
let rightMid = mid.slice(rootIdx + 1);
// 将右子树的后、中遍历序列加入执行队列
queue.push([rightPost, rightMid]);
}
}
Java算法源码
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String post = sc.next();
String mid = sc.next();
System.out.println(getResult(post, mid));
}
/**
* @param post 后序遍历结果
* @param mid 中序遍历结果
* @return 层序遍历结果
*/
public static String getResult(String post, String mid) {
// 广度优先搜索的执行队列,先加入左子树,再加入右子树
LinkedList<String[]> queue = new LinkedList<>();
// 层序遍历出来的元素存放在ans中
ArrayList<Character> ans = new ArrayList<>();
devideLR(post, mid, queue, ans);
while (queue.size() > 0) {
String[] tmp = queue.removeFirst();
devideLR(tmp[0], tmp[1], queue, ans);
}
StringBuilder sb = new StringBuilder();
for (Character c : ans) {
sb.append(c);
}
return sb.toString();
}
/**
* 本方法用于从后序遍历、中序遍历序列中分离出:根,以及其左、右子树的后序、中序遍历序列
*
* @param post 后序遍历结果
* @param mid 中序遍历结果
* @param queue BFS的执行队列
* @param ans 题解
*/
public static void devideLR(
String post, String mid, LinkedList<String[]> queue, ArrayList<Character> ans) {
// 后序遍历的最后一个元素就是根
char rootEle = post.charAt(post.length() - 1);
// 将根加入题解
ans.add(rootEle);
// 在中序遍历中找到根的位置rootIdx,那么该位置左边就是左子树,右边就是右子树
int rootIdx = mid.indexOf(rootEle);
// 左子树长度,左子树是中序遍历的0~rootIdx-1范围,长度为rootIdx
int leftLen = rootIdx;
// 如果存在左子树,即左子树长度大于0
if (leftLen > 0) {
// 则从后序遍历中,截取出左子树的后序遍历
String leftPost = post.substring(0, leftLen);
// 从中序遍历中,截取出左子树的中序遍历
String leftMid = mid.substring(0, rootIdx);
// 将左子树的后、中遍历序列加入执行队列
queue.addLast(new String[] {leftPost, leftMid});
}
// 如果存在右子树,即右子树长度大于0
if (post.length() - 1 - leftLen > 0) {
// 则从后序遍历中,截取出右子树的后序遍历
String rightPost = post.substring(leftLen, post.length() - 1);
// 从中序遍历中,截取出右子树的中序遍历
String rightMid = mid.substring(rootIdx + 1);
// 将右子树的后、中遍历序列加入执行队列
queue.addLast(new String[] {rightPost, rightMid});
}
}
}
Python算法源码
# 输入获取
post, mid = input().split()
def devideLR(post, mid, queue, ans):
"""
本方法用于从后序遍历、中序遍历序列中分离出:根,以及其左、右子树的后序、中序遍历序列
:param post: 后序遍历结果
:param mid: 中序遍历结果
:param queue: BFS的执行队列
:param ans: 题解
"""
# 后序遍历的最后一个元素就是根
rootEle = post[-1]
# 将根加入题解
ans.append(rootEle)
# 在中序遍历中找到根的位置rootIdx,那么该位置左边就是左子树,右边就是右子树
rootIdx = mid.find(rootEle)
# 左子树长度,左子树是中序遍历的0~rootIdx-1范围,长度为rootIdx
leftLen = rootIdx
# 如果存在左子树,即左子树长度大于0
if leftLen > 0:
leftPost = post[:leftLen] # 则从后序遍历中,截取出左子树的后序遍历
leftMid = mid[:rootIdx] # 从中序遍历中,截取出左子树的中序遍历
queue.append([leftPost, leftMid]) # 将左子树的后、中遍历序列加入执行队列
# 如果存在右子树,即右子树长度大于0
if len(post) - 1 - leftLen > 0:
rightPost = post[leftLen:-1] # 则从后序遍历中,截取出右子树的后序遍历
rightMid = mid[rootIdx + 1:] # 从中序遍历中,截取出右子树的中序遍历
queue.append([rightPost, rightMid]) # 将右子树的后、中遍历序列加入执行队列
# 算法入口
def getResult(post, mid):
# 广度优先搜索的执行队列,先加入左子树,再加入右子树
queue = []
# 层序遍历出来的元素存放在ans中
ans = []
devideLR(post, mid, queue, ans)
while len(queue) > 0:
post, mid = queue.pop(0)
devideLR(post, mid, queue, ans)
return "".join(ans)
# 算法调用
print(getResult(post, mid))
C算法源码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
/** 链表定义 **/
typedef struct ListNode {
char post[27];
char mid[27];
struct ListNode *next;
} ListNode;
typedef struct LinkedList {
int size;
ListNode *head;
ListNode *tail;
} LinkedList;
LinkedList *new_LinkedList() {
LinkedList *link = (LinkedList *) malloc(sizeof(LinkedList));
link->size = 0;
link->head = NULL;
link->tail = NULL;
return link;
}
void addLast_LinkedList(LinkedList *link, char *post, char *mid) {
ListNode *node = (ListNode *) malloc(sizeof(ListNode));
strcpy(node->post, post);
strcpy(node->mid, mid);
node->next = NULL;
if (link->size == 0) {
link->head = node;
link->tail = node;
} else {
link->tail->next = node;
link->tail = node;
}
link->size++;
}
ListNode *removeFirst_LinkedList(LinkedList *link) {
if (link->size == 0) exit(-1);
ListNode *removed = link->head;
if (link->size == 1) {
link->head = NULL;
link->tail = NULL;
} else {
link->head = link->head->next;
}
link->size--;
return removed;
}
// res记录题解
char res[27];
int res_size = 0;
/*!
* 字符串截取(左闭右开)
* @param s 字符串
* @param start 起始位置(包含)
* @param end 结束位置(不包含)
* @return 指定区间的子串
*/
char *subString(char *s, int start, int end) {
int len = end - start;
char *tmp = (char *) calloc(len + 1, sizeof(char));
strncat(tmp, s + start, len);
return tmp;
}
/*!
* 本方法用于从后序遍历、中序遍历序列中分离出:根,以及其左、右子树的后序、中序遍历序列
* @param post 后序遍历结果
* @param mid 中序遍历结果
* @param queue BFS的执行队列
*/
void devideLR(char *post, char *mid, LinkedList *queue) {
// 后序遍历的最后一个元素就是根
char rootEle = post[strlen(post) - 1];
// 将根加入题解
res[res_size++] = rootEle;
// 在中序遍历中找到根的位置rootIdx,那么该位置左边就是左子树,右边就是右子树
int rootIdx = strchr(mid, rootEle) - mid;
// 左子树长度,左子树是中序遍历的0~rootIdx-1范围,长度为rootIdx
// 如果存在左子树,即左子树长度大于0
if (rootIdx > 0) {
// 则从后序遍历中,截取出左子树的后序遍历
char* leftPost = subString(post, 0, rootIdx);
// 从中序遍历中,截取出左子树的中序遍历
char* leftMid = subString(mid, 0, rootIdx);
// 将左子树的后、中遍历序列加入执行队列
addLast_LinkedList(queue, leftPost, leftMid);
}
// 如果存在右子树,即右子树长度大于0
if (strlen(post) - 1 - rootIdx > 0) {
// 则从后序遍历中,截取出右子树的后序遍历
char* rightPost = subString(post, rootIdx, strlen(post) - 1);
// 从中序遍历中,截取出右子树的中序遍历
char* rightMid = subString(mid, rootIdx + 1, strlen(mid));
// 将右子树的后、中遍历序列加入执行队列
addLast_LinkedList(queue, rightPost, rightMid);
}
}
int main() {
char post[27];
char mid[27];
scanf("%s %s", post, mid);
// 广度优先搜索的执行队列,先加入左子树,再加入右子树
LinkedList *queue = new_LinkedList();
// 层序遍历出来的元素存放在res中
devideLR(post, mid, queue);
while (queue->size > 0) {
ListNode* node = removeFirst_LinkedList(queue);
devideLR(node->post, node->mid, queue);
}
puts(res);
return 0;
}
免责声明:
评论0