题目描述
算法工程师小明面对着这样一个问题 ,需要将通信用的信道分配给尽量多的用户:
信道的条件及分配规则如下:
- 所有信道都有属性:”阶”。阶为 r的信道的容量为 2^r比特;
- 所有用户需要传输的数据量都一样:D比特;
- 一个用户可以分配多个信道,但每个信道只能分配给一个用户;
- 只有当分配给一个用户的所有信道的容量和>=D,用户才能传输数据;
给出一组信道资源,最多可以为多少用户传输数据?
输入描述
第一行,一个数字 R。R为最大阶数。
0<=R<20
第二行,R+1个数字,用空格隔开。代表每种信道的数量 Ni。按照阶的值从小到大排列。
0<=i<=R,0<=Ni<1000.
第三行,一个数字 D。D为单个用户需要传输的数据量。
0<D<1000000
输出描述
一个数字(代表最多可以供多少用户传输数据)
用例
| 输入 | 5 10 5 0 1 3 2 30 |
| 输出 | 4 |
| 说明 | 无 |
题目解析
这题是真的难,可能是我没想到点子上吧,解法想了一晚上,第二天带着两个黑眼圈,灵光一闪,有了下面的解法。
首先,题目的意思,我一开始就没看懂,后面琢磨来琢磨去,分析题目的意思应该是:
第一行输入的r表示第二行的最大阶数,第二行又是r+1个数,也就是说:
比如第一行输入的r=5,则第二行会输入r+1=6个数,如下
- 第一个数10,的阶是0,即容量是2^0的信道有10个
- 第二个数 5,的阶是1,即容量是2^1的信道有5个
- 第三个数 0,的阶是2,即容量是2^2的信道有0个
- 第四个数 1,的阶是3,即容量是2^3的信道有1个
- 第五个数 3,的阶是4,即容量是2^4的信道有3个
- 第六个数 2,的阶是5,即容量是2^5的信道有2个
题目要求从上面给定的多种信道中,任意挑选几个(未使用的)进行组合,让组合之和大于等于第三行输入的D值,问这种组合最多能有多少个?
这题,我一开始想要dfs求得所有无重复使用信道的组合,但是发现只能求出一类,而无法求出多类。大家可以试试,看看dfs行不行。
之后我又想,想要最多的组合情况,那么信道就要省着用,比如每个用户需要至少D容量的信道组合,那么我们就尽可能地构造出容量准确为D的信道组合,
比如 16 + 8 + 4 + 2 = 30,因此我们可以选择:
一个阶4的信道,一个阶3的信道,一个阶2的信道,一个阶1的信道。
但是由于没有阶2的信道,因此我们可以将对于阶2的需求降级,变为两个阶1的信道,也就是说最终选择是:
一个阶4的信道,一个阶3的信道,三个阶1的信道。
即 16 + 8 + 2 * 3 = 30
另外,如果单个信道容量就能满足D,比如阶5的单个信道容量是32,虽然此时浪费了一些,但是一个信道只能给一个用户使用,因此为了避免更大的浪费,32的信道就可以单独组合,而不需要组合其他信道。
那么如何能准确的构造出容量为30的信道组合呢?
题目中信道容量是2^n,因此我有了如下思路:
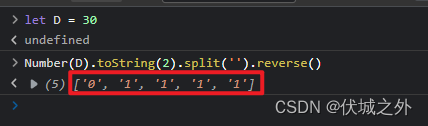
首先,我们将D值转为二进制,然后转为字符数组,再反序,让D和N的阶数方向保持一致,
比如D=30,可以转为[0, 1, 1, 1, 1] 的反序二进制值的个数数组,该数组的含义是
- 2^0有0个
- 2^1有1个
- 2^2有1个
- 2^3有1个
- 2^4有1个
而输入的第二行,也就是N也可以看成反序二进制数的个数数组: [10, 5, 0, 1, 3, 2]
该数组的含义是:
- 2^0有10个
- 2^1有5个
- 2^2有0个
- 2^3有1个
- 2^4有3个
- 2^5有2个
如果想从N中选几个信道组成和为D的组合,那么不就是N和D的二进制值个数求差吗?
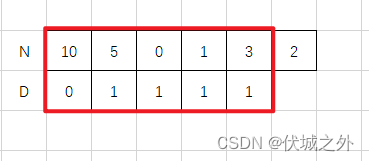
我们只需要比较D.length范围的内,而超出D.length范围的N[i]其实就是单个信道就足以满足一个用户通信的。
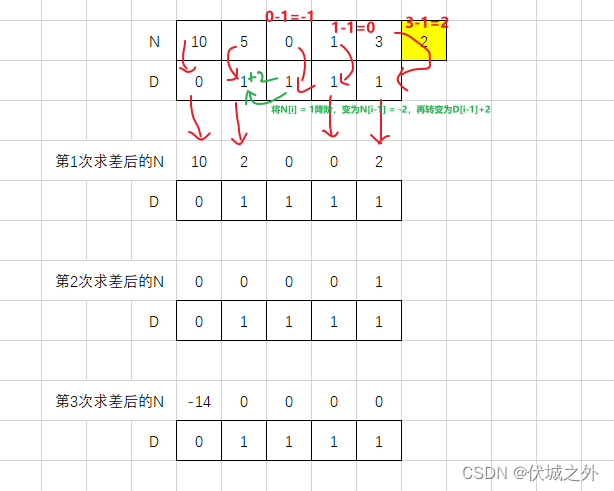
如上图所示,如果每次求差后,N[0] >= 0,则表示可以构造出一个和为30的信道组合。
但是N[0] < 0 只能表示无法构造出一个和准确为30的的信道组合,但是却还是有可能构造出一个和大于30的信道组合
程序输入
5
10 5 0 1 3 2
47
对应的N和D如下

直到N[i]完全抵消了负值结束,然后count++。也可能N[i]到最后也没有抵消完负值,此时说明无法构造出一个和大于30的信道组合,整个程序结束。
以下代码比较难以理解,建议大家debug模式帮助理解,可以监听几个关键值
- N:输入的第二行转化来信道个数数组
- D2:输入的第三行D转化来的构造出准确D容量的信道个数数组
- i:循环变量
- minus:N[i]和D2[i]的差值
- count:满足要求的信道组合个数
2023.10.10
上面举得例子
5
10 5 0 1 3 2
47
进行二进制减法时存在问题
如下图所示,在进行第二次减法时
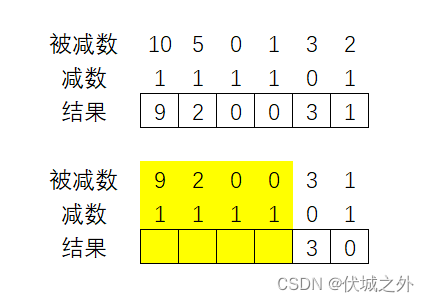
之前的策略时,总是向低位借,因此最后借债都会压到被减数的阶0上,之后再将阶0上的借债,转移不停转移到高位,因此会得到结果如下
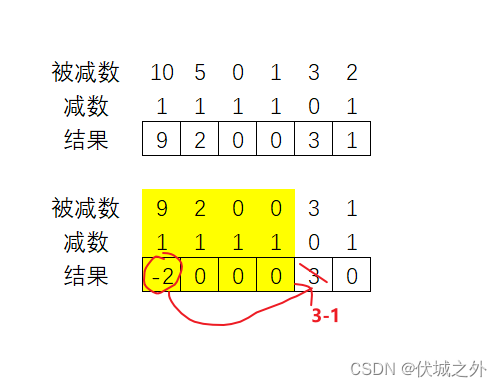
但是这种策略不是最优的,因为我们可以看下图
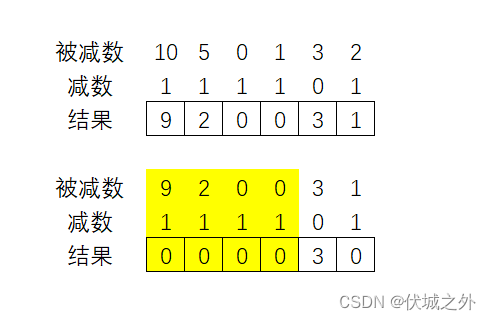
其中 被减数的标黄部分,经过计算,是可以确定小于 减数的标黄部分的,因此即使我们向低位借,最终还是不够,最后反过来还是要向高位借。
而二进制数,一个高位是可以直接满足前面的所有低位的,什么意思呢?看下图
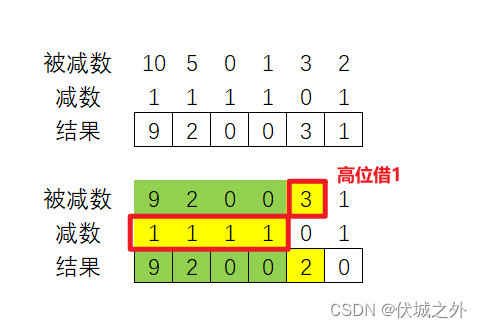
我们此时直接从被减数红框高位中借1,就可以满足 减数红框中所有位之和。
此时被减数的 绿色低位部分 得到了保留,避免了浪费。
Python算法源码
# 输入获取
R = int(input())
N = list(map(int, input().split()))
D = int(input())
def calc_sub(bin1):
ans = 0
for i in range(len(bin1)):
ans += bin1[i] * (1 << i)
return ans
def binary_sub(minuend, subtrahend):
"""
二进制减法
:param minuend: 被减数
:param subtrahend: 减数
:return: 被减数是否为正数
"""
# 进行减法运算逻辑, 从高位开始
i = len(minuend) - 1
while i >= 0:
if minuend[i] >= subtrahend[i]:
# 如果对应位的信道数足够,则直接相减
minuend[i] -= subtrahend[i]
else:
# 如果对应位的信道数不足,此时有两种策略,一是向低位借,一是向高位借
# 具体向哪里借,需要看 minuend 的 [0,i] 低位部分是否能够承载 subtrahend[0, i] 低位部分
if calc_sub(minuend[0:i + 1]) < calc_sub(subtrahend[0:i + 1]):
# 如果minuend 的 [0,i]不能承载,则向高位借,即从j=i+1位开始借
j = i + 1
while j < len(minuend):
if minuend[j] > 0:
# 如果高位 j 有信道可借,则借
minuend[j] -= 1
return True
else:
# 否则继续向更高位探索
j += 1
# 如果所有高位都没有富余信道数,则说明减法结果为负数
return False
else:
# 如果minuend 的 [0,i]可以承载,则向低位借(可以避免浪费)
# 此时minuend[i]为负数,表示欠债
minuend[i] -= subtrahend[i]
# 将当前阶位的欠债,转移到前面的低阶位上,注意转移时,欠债x2
minuend[i - 1] += minuend[i] << 1
# 转移后,当前阶位的欠债变为0
minuend[i] = 0
i -= 1
return True
# 算法入口
def getResult():
# 将D值转化为二进制形式,并且为了和N[]的阶位进行对应,这里将D的二进制进行了反转
subtrahend = list(map(int, str(bin(D))[2:]))
subtrahend.reverse()
# count记录N能承载几个D
count = 0
# N中高阶信道的单个信道就能满足D,因此这些高阶信道有几个,即能承载几个D
for i in range(len(subtrahend), R + 1):
# R ~ subtrahend.length 阶的单个信道就能承载一个D,因此这些信道有几个,就能承载几个D
count += N[i]
# 0 ~ subtrahend.length - 1 阶的单个信道无法承载一个D,因此这些阶需要组合起来才能承载一个D
minuend = N[0:len(subtrahend)]
while len(minuend) < len(subtrahend):
minuend.append(0)
# 进行二进制减法
while binary_sub(minuend, subtrahend):
count += 1
return count
# 算法调用
print(getResult())Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int R = sc.nextInt();
int[] N = new int[R + 1];
for (int i = 0; i <= R; i++) {
N[i] = sc.nextInt();
}
int D = sc.nextInt();
System.out.println(getResult(R, N, D));
}
public static int getResult(int R, int[] N, int D) {
// 将D值转化为二进制形式,并且为了和N[]的阶位进行对应,这里将D的二进制进行了反转
int[] subtrahend =
Arrays.stream(new StringBuilder(Integer.toBinaryString(D)).reverse().toString().split(""))
.mapToInt(Integer::parseInt)
.toArray();
// count记录N能承载几个D
int count = 0;
// N中高阶信道的单个信道就能满足D,因此这些高阶信道有几个,即能承载几个D
for (int i = R; i >= subtrahend.length; i--) {
// R ~ subtrahend.length 阶的单个信道就能承载一个D,因此这些信道有几个,就能承载几个D
count += N[i];
}
// 0 ~ subtrahend.length - 1 阶的单个信道无法承载一个D,因此这些阶需要组合起来才能承载一个D
int[] minuend = Arrays.copyOfRange(N, 0, subtrahend.length);
// 进行二进制减法
while (binary_sub(minuend, subtrahend)) {
count++;
}
return count;
}
/**
* 二进制减法
*
* @param minuend 被减数
* @param subtrahend 减数
* @return 被减数是否为正数
*/
public static boolean binary_sub(int[] minuend, int[] subtrahend) {
// 进行减法运算逻辑, 从高位开始
for (int i = minuend.length - 1; i >= 0; i--) {
if (minuend[i] >= subtrahend[i]) {
// 如果对应位的信道数足够,则直接相减
minuend[i] -= subtrahend[i];
} else {
// 如果对应位的信道数不足,此时有两种策略,一是向低位借,一是向高位借
// 具体向哪里借,需要看 minuend 的 [0,i] 低位部分是否能够承载 subtrahend[0, i] 低位部分
if (calc_bin(Arrays.copyOfRange(minuend, 0, i + 1))
< calc_bin(Arrays.copyOfRange(subtrahend, 0, i + 1))) {
// 如果minuend 的 [0,i]不能承载,则向高位借,即从j=i+1位开始借
int j = i + 1;
while (j < minuend.length) {
if (minuend[j] > 0) {
// 如果高位 j 有信道可借,则借
minuend[j] -= 1;
return true;
} else {
// 否则继续向更高位探索
j += 1;
}
}
// 如果所有高位都没有富余信道数,则说明减法结果为负数
return false;
} else {
// 如果minuend 的 [0,i]可以承载,则向低位借(向低位借,可以避免浪费)
// 此时minuend[i]为负数,表示欠债
minuend[i] -= subtrahend[i];
// 将当前阶位的欠债,转移到前面的低阶位上,注意转移时,欠债x2
minuend[i - 1] += minuend[i] << 1;
// 转移后,当前阶位的欠债变为0
minuend[i] = 0;
}
}
}
return true;
}
public static int calc_bin(int[] bin) {
int ans = 0;
for (int i = 0; i < bin.length; i++) {
ans += bin[i] * (1 << i);
}
return ans;
}
}
JavaScript算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
// Write your code here
const R = parseInt(await readline());
const N = (await readline()).split(" ").map(Number);
const D = parseInt(await readline());
console.log(getResult(R, N, D));
})();
function getResult(R, N, D) {
// 将D值转化为二进制形式,并且为了和N[]的阶位进行对应,这里将D的二进制进行了反转
const subtrahend = Number(D).toString(2).split("").map(Number).reverse();
// count记录N能承载几个D
let count = 0;
// N中高阶信道的单个信道就能满足D,因此这些高阶信道有几个,即能承载几个D
for (let i = R; i >= subtrahend.length; i--) {
// R ~ subtrahend.length 阶的单个信道就能承载一个D,因此这些信道有几个,就能承载几个D
count += N[i];
}
// 0 ~ subtrahend.length - 1 阶的单个信道无法承载一个D,因此这些阶需要组合起来才能承载一个D
const minuend = N.slice(0, subtrahend.length);
while (minuend.length < subtrahend.length) {
minuend.push(0);
}
// 进行二进制减法
while (binary_sub(minuend, subtrahend)) {
count++;
}
return count;
}
/**
* 进行二进制减法
* @param {*} minuend 被减数
* @param {*} subtrahend 减数
* @returns 被减数是否为正数
*/
function binary_sub(minuend, subtrahend) {
// 进行减法运算逻辑, 从高位开始
for (let i = minuend.length - 1; i >= 0; i--) {
if (minuend[i] >= subtrahend[i]) {
// 如果对应位的信道数足够,则直接相减
minuend[i] -= subtrahend[i];
} else {
// 如果对应位的信道数不足,此时有两种策略,一是向低位借,一是向高位借
// 具体向哪里借,需要看 minuend 的 [0,i] 低位部分是否能够承载 subtrahend[0, i] 低位部分
if (
calc_sub(minuend.slice(0, i + 1)) < calc_sub(subtrahend.slice(0, i + 1))
) {
// 如果minuend 的 [0,i]不能承载,则向高位借,即从j=i+1位开始借
let j = i + 1;
while (j < minuend.length) {
if (minuend[j] > 0) {
// 如果高位 j 有信道可借,则借
minuend[j] -= 1;
return true;
} else {
// 否则继续向更高位探索
j += 1;
}
}
// 如果所有高位都没有富余信道数,则说明减法结果为负数
return false;
} else {
// 如果minuend 的 [0,i]可以承载,则向低位借(向低位借,可以避免浪费)
// 此时minuend[i]为负数,表示欠债
minuend[i] -= subtrahend[i];
// 将当前阶位的欠债,转移到前面的低阶位上,注意转移时,欠债x2
minuend[i - 1] += minuend[i] << 1;
// 转移后,当前阶位的欠债变为0
minuend[i] = 0;
}
}
}
return true;
}
function calc_sub(bin) {
let ans = 0;
for (let i = 0; i < bin.length; i++) {
ans += bin[i] * (1 << i);
}
return ans;
}
C算法源码
#include <stdio.h>
#define MAX_SIZE 20
int getResult(int R, int N[], int D);
int binary_sub(int minuend[], int subtrahend[], int size);
int calc_bin(const int bin[], int bin_size);
int main() {
int R;
scanf("%d", &R);
int N[MAX_SIZE] = {0};
for(int i=0; i<=R; i++) {
scanf("%d", &N[i]);
}
int D;
scanf("%d", &D);
printf("%dn", getResult(R, N, D));
return 0;
}
int getResult(int R, int N[], int D) {
int subtrahend[50];
int subtrahend_size = 0;
// 将D值转化为二进制形式,并且为了和N[]的阶位进行对应,这里将D的二进制进行了反转
while(D > 0) {
subtrahend[subtrahend_size++] = D % 2;
D /= 2;
}
// count记录N能承载几个D
int count = 0;
// N中高阶信道的单个信道就能满足D,因此这些高阶信道有几个,即能承载几个D
for(int i = R; i >= subtrahend_size; i--) {
// R ~ subtrahend.length 阶的单个信道就能承载一个D,因此这些信道有几个,就能承载几个D
count += N[i];
}
// 0 ~ subtrahend.length - 1 阶的单个信道无法承载一个D,因此这些阶需要组合起来才能承载一个D
int minuend[subtrahend_size];
for(int i=0; i<subtrahend_size; i++) {
minuend[i] = N[i];
}
// 进行二进制减法
while(binary_sub(minuend, subtrahend, subtrahend_size)) {
count++;
}
return count;
}
/*!
*
* @param minuend 被减数
* @param subtrahend 减数
* @param size 被减数和件数的二进制位数
* @return 减法运算后,被减数是否为正数
*/
int binary_sub(int minuend[], int subtrahend[], int size) {
// 进行减法运算逻辑, 从高位开始
for(int i=size - 1; i >= 0; i--) {
if(minuend[i] >= subtrahend[i]) {
// 如果对应位的信道数足够,则直接相减
minuend[i] -= subtrahend[i];
} else {
// 如果对应位的信道数不足,此时有两种策略,一是向低位借,一是向高位借
// 具体向哪里借,需要看 minuend 的 [0,i] 低位部分是否能够承载 subtrahend[0, i] 低位部分
if(calc_bin(minuend, i+1) < calc_bin(subtrahend, i+1)) {
// 如果minuend 的 [0,i]不能承载,则向高位借,即从j=i+1位开始借
int j = i + 1;
while (j < size) {
if(minuend[j] > 0) {
// 如果高位 j 有信道可借,则借
minuend[j] -= 1;
return 1;
} else {
// 否则继续向更高位探索
j += 1;
}
}
// 如果所有高位都没有富余信道数,则说明减法结果为负数
return 0;
} else {
// 如果minuend 的 [0,i]可以承载,则向低位借(向低位借,可以避免浪费)
// 此时minuend[i]为负数,表示欠债
minuend[i] -= subtrahend[i];
// 将当前阶位的欠债,转移到前面的低阶位上,注意转移时,欠债x2
minuend[i-1] += minuend[i] << 1;
// 转移后,当前阶位的欠债变为0
minuend[i] = 0;
}
}
}
return 1;
}
int calc_bin(const int bin[], int bin_size) {
int ans = 0;
for(int i=0; i<bin_size; i++) {
ans += bin[i] * (1 << i);
}
return ans;
}
免责声明:
评论0