题目描述
某地有N个广播站,站点之间有些有连接,有些没有。有连接的站点在接受到广播后会互相发送。
给定一个N*N的二维数组matrix,数组的元素都是字符’0’或者’1’。
matrix[i][j] = ‘1’, 代表i和j站点之间有连接,
matrix[i][j] = ‘0’, 代表没连接,
现在要发一条广播,问初始最少给几个广播站发送,才能保证所有的广播站都收到消息。
输入描述
从stdin输入,共一行数据,表示二维数组的各行,用逗号分隔行。保证每行字符串所含的字符数一样的。
比如:110,110,001。
输出描述
返回初始最少需要发送广播站个数
用例
| 输入 | 110,110,001 |
| 输出 | 2 |
| 说明 | 站点1和站点2直接有连接,站点3和其他的都没连接,所以开始至少需要给两个站点发送广播。 |
| 输入 |
100,010,001 |
| 输出 | 3 |
| 说明 | 3台服务器互不连接,所以需要分别广播这3台服务器。 |
| 输入 |
11,11 |
| 输出 | 1 |
| 说明 | 2台服务器相互连接,所以只需要广播其中一台服务器 |
题目解析
题目中说:“有连接的站点在接受到广播后会互相发送。”
这表明了如果matrix[i][j] = ‘1’,则必然matrix[j][i] = ‘1’,即如下图中二维矩阵中元素值,会沿左上右下对角线轴对称
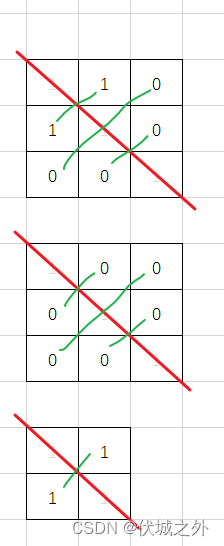
因此,解决本题,我们只需要看对角线的一侧即可。
有了上面的前提,下面我们可以通过画图来解决此题
比如输入:1101,1100,0011,1011,画图如下
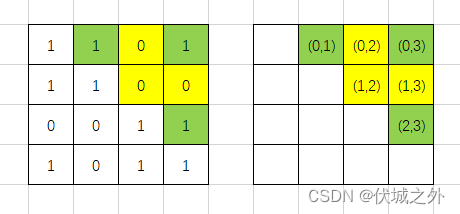
因此可得联通图如下
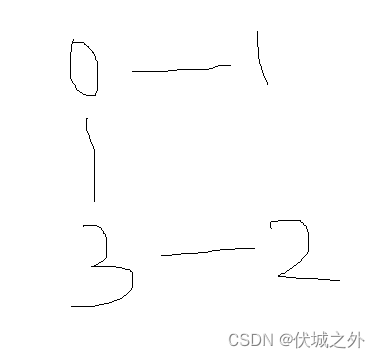
由于站点之间的连接是双向的,因此上面例子只要给一个站点发送广播,所有站点就都能收到广播了
再比如,输入11010,11000,00110,10110,00001
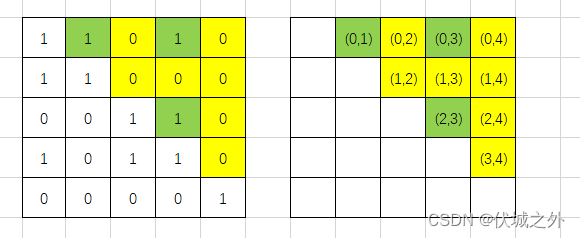
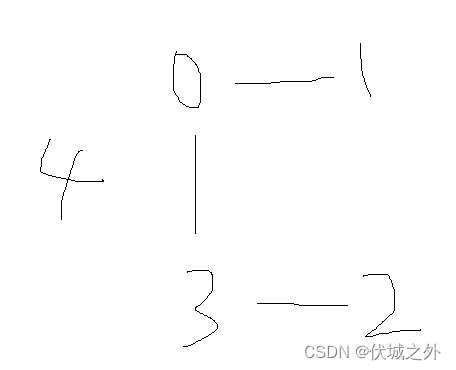
此时0,1,2,3站点是互联的,4没有任何连接,因此我们需要给至少两个站点发送广播。
那么如何才能构建上面这种连通图呢?
最好的方式就是创建 并查集 结构。
并查集本身其实就是一个数组,数组的索引指代站点,数组的元素值指代当前索引站点的祖先站点。
比如上面例子中,我们有5个站点,因此我们可以创建一个长度为5的数组arr,初始时,每个站点都可以视为互不相连的,即每个站点的祖先站点都是自己
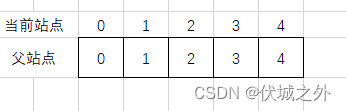
我们开始遍历输入的二维数组对角线一侧的站点连接情况,来更新上面的并查集结构,实现代码如下
// 输入是一个n*n的二维矩阵
for(let i=0; i<n; i++) {
for(let j=i+1; j<n; j++) {
if(matrix[i][j] === '1') 更新并查集
}
}
matrix[0][1] = 1,因此我们将站点1的父站点更新为0,即arr[1] = 0
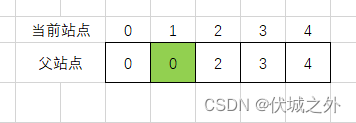
matrix[0][3] = 1,因此我们将站点3的父站点更新为0,即arr[3] = 0
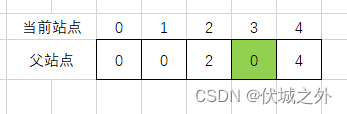
matrix[2][3] = 1,因此我们将站点3的父站点更新为2,但是由于站点3已经更新过父站点为0了,因此我们此时再次更新,只会覆抹除掉站点3和站点0之间的父子关系,为了避免这种情况,我们可以先找到站点的3的祖宗站点(即为站点0),然后将祖先站点0的父站点更新为2
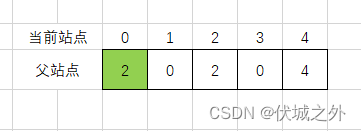
有人可能会感觉到疑惑,如果这样更新的话,岂不是影响了站点1,因为站点1的父站点是站点0,现在站点0的父站点更新为了站点2,那么也就意味着站点1的祖先站点变为站点2?
我们再回头思考下,我们使用并查集的目的是啥,是构造连通图,而不是构造准确的父子关系,我们将上面并查集结构转为连通图看看
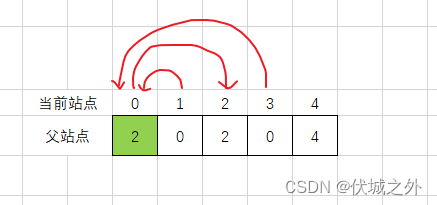
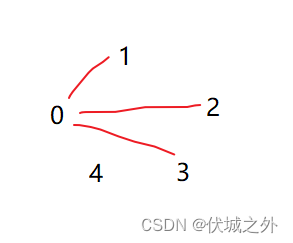
发现,就是我们想要的。
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const matrix = line.split(",").map((str) => str.split(""));
console.log(getMinCount(matrix));
});
function getMinCount(matrix) {
const n = matrix.length;
const ufs = new UnionFindSet(n);
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
if (matrix[i][j] === "1") {
ufs.union(i, j);
}
}
}
return ufs.count;
}
class UnionFindSet {
constructor(n) {
this.fa = new Array(n).fill(true).map((_, idx) => idx);
this.count = n; // 初始时各站点互不相连,互相独立,因此需要给n个站点发送广播
}
// 查x站点对应的顶级祖先站点
find(x) {
while (x !== this.fa[x]) {
x = this.fa[x];
}
return x;
}
// 合并两个站点,其实就是合并两个站点对应的顶级祖先节点
union(x, y) {
let x_fa = this.find(x);
let y_fa = this.find(y);
if (x_fa !== y_fa) { // 如果两个站点祖先相同,则在一条链上,不需要合并
this.fa[y_fa] = x_fa; // 合并站点,即让某条链的祖先指向另一条链的祖先
this.count--; // 一旦两个站点合并,则发送广播次数减1
}
}
}
以上算法,还可以继续优化find逻辑,当前find逻辑,找某个站点的祖先,都会从所在链的自身位置开始向上逐级查找,这个过程其实也找到了同一链上它之后的站点的祖先
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const matrix = line.split(",").map((str) => str.split(""));
console.log(getMinCount(matrix));
});
function getMinCount(matrix) {
const n = matrix.length;
const ufs = new UnionFindSet(n);
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
if (matrix[i][j] === "1") {
ufs.union(i, j);
}
}
}
// console.log(ufs.fa);
return ufs.count;
}
class UnionFindSet {
constructor(n) {
this.fa = new Array(n).fill(true).map((_, idx) => idx);
this.count = n;
}
find(x) {
if (x !== this.fa[x]) {
this.fa[x] = this.find(this.fa[x]);
return this.fa[x];
}
return x;
}
union(x, y) {
let x_fa = this.find(x);
let y_fa = this.find(y);
if (x_fa !== y_fa) {
this.fa[y_fa] = x_fa;
this.count--;
}
}
}
我们可以将while循环改为递归,将每次递归的结果(祖先站点)更新为递归站点的父站点。
还有一道相同意思的题目:
有兴趣的小伙伴可以试试
Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String[] matrix = sc.nextLine().split(",");
System.out.println(getResult(matrix));
}
public static int getResult(String[] matrix) {
int n = matrix.length;
UnionFindSet ufs = new UnionFindSet(n);
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (matrix[i].charAt(j) == '1') {
ufs.union(i, j);
}
}
}
return ufs.count;
}
}
// 并查集实现
class UnionFindSet {
int[] fa;
int count;
public UnionFindSet(int n) {
this.fa = new int[n];
for (int i = 0; i < n; i++) fa[i] = i;
this.count = n;
}
public int find(int x) {
if (x != this.fa[x]) {
this.fa[x] = this.find(this.fa[x]);
return this.fa[x];
}
return x;
}
public void union(int x, int y) {
int x_fa = this.find(x);
int y_fa = this.find(y);
if (x_fa != y_fa) {
this.fa[y_fa] = x_fa;
this.count--;
}
}
}
Python算法源码
# 输入获取
matrix = input().split(",")
# 并查集实现
class UnionFindSet:
def __init__(self, n):
self.fa = [i for i in range(n)]
self.count = n
def find(self, x):
if x != self.fa[x]:
self.fa[x] = self.find(self.fa[x])
return self.fa[x]
return x
def union(self, x, y):
x_fa = self.find(x)
y_fa = self.find(y)
if x_fa != y_fa:
self.fa[y_fa] = x_fa
self.count -= 1
# 算法入口
def getResult(matrix):
n = len(matrix)
ufs = UnionFindSet(n)
for i in range(n):
for j in range(i + 1, n):
if matrix[i][j] == "1":
ufs.union(i, j)
return ufs.count
# 算法调用
print(getResult(matrix))
C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 10000
/** 并查集定义 **/
typedef struct {
int *fa;
int count;
} UFS;
UFS *new_UFS(int n) {
UFS *ufs = (UFS *) malloc(sizeof(UFS));
ufs->fa = (int *) malloc(sizeof(int) * n);
for (int i = 0; i < n; i++) {
ufs->fa[i] = i;
}
ufs->count = n;
return ufs;
}
int find_UFS(UFS *ufs, int x) {
if (x != ufs->fa[x]) {
ufs->fa[x] = find_UFS(ufs, ufs->fa[x]);
return ufs->fa[x];
}
return x;
}
void union_UFS(UFS *ufs, int x, int y) {
int x_fa = find_UFS(ufs, x);
int y_fa = find_UFS(ufs, y);
if (x_fa != y_fa) {
ufs->fa[y_fa] = x_fa;
ufs->count--;
}
}
/** 算法逻辑 **/
char matrix[MAX_SIZE][MAX_SIZE];
int main() {
int n = 0;
while (scanf("%[^\,n]", matrix[n++])) {
if (getchar() != ',') break;
}
UFS *ufs = new_UFS(n);
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (matrix[i][j] == '1') {
union_UFS(ufs, i, j);
}
}
}
printf("%dn", ufs->count);
return 0;
}免责声明:
评论0