题目描述
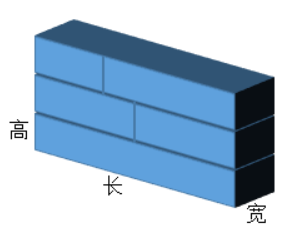
有一堆长方体积木,它们的宽度和高度都相同,但长度不一。
小橙想把这堆积木叠成一面墙,墙的每层可以放一个积木,也可以将两个积木拼接起来,要求每层的长度相同。
若必须用完这些积木,叠成的墙最多为多少层?
输入描述
输入为一行,为各个积木的长度,数字为正整数,并由空格分隔。积木的数量和长度都不超过5000。
输出描述
输出一个数字,为墙的最大层数,如果无法按要求叠成每层长度一致的墙,则输出-1。
用例
| 输入 | 3 6 6 3 |
| 输出 | 3 |
| 说明 | 可以每层都是长度3和6的积木拼接起来,这样每层的长度为9,层数为2;也可以其中两层直接用长度6的积木,两个长度3的积木拼接为一层,这样层数为3,故输出3。 |
| 输入 | 1 4 2 3 6 |
| 输出 | -1 |
| 说明 | 无法用这些积木叠成每层长度一致的墙,故输出-1。 |
题目解析
本题限制了一层最多只能有两个积木,最少有一个积木。
如果没有这个上面限制条件,那么本题需要换另一种解法:
有了这个限制,本题的难度就降低很多了,我的解题思路如下:
- 如果只有一个积木,那么最大高度就是1
- 如果只有两个积木,那么
- 两个积木长度相同时,最大高度为2
- 两个积木长度不同时,最大高度为1
- 如果有三个及以上积木,我的思路如下,假设输入的积木长度数组为nums:
- 将所有积木按照长度降序
- 求出一层长度的取值范围,一层长度至少为nums[0],至多为nums[0] + nums[1],由于nums已经降序,因此nums[0]就是最长的积木,nums[1]就是第二长的积木
- 遍历nums[0] ~ nums[0] + nums[1]的值length作为一层长度去尝试:
定义两个指针L,R,初始时L=0,R=nums.length-1
- 如果nums[L] == length,则说明L积木可以独立一层,层高+1,然后L++,如此循环,直到nums[L] < length
接着,计算nums[L] + nums[R]的和sum,
- 如果sum != length,则有两种可能:
- 假设nums[l] + nums[r] > length,则必然nums[l] + nums[r-1] > length,因为nums已降序,nums[r-1] >= nums[r],即必然l积木无法和其他积木组成一层
- 假设nums[l] + nums[r] < length,则必然nums[l+1] + nums[r] < length,因为nums已降序,nums[l+1] <= nums[l],即必然r积木无法和其他积木组成一层
- 如果sum == length,则L,R积木组成一层,层高+1,然后继续尝试L++,R–
本题要求最大的高度,那么一层的长度就要尽量小,而上面的length是从nums[0] ~ nums[0] + nums[1],因此一旦发现了遍历的length,可以让所有的积木搭建起来,那么该length就是最优的,即能够形成最大高度的。
2023.10.13
上面逻辑分析时:
假设nums已经降序,则一层长度范围是: nums[0] ~ nums[0] + nums[1],nums.length > 1
这里对于一层的长度最大值 nums[0] + nums[1] 是有冗余的
因为,一旦一层长度定义为 nums[0] + nums[1],
则可以确定的是任意两个积木长度之和:
nums[i] + nums[j] 必然小于 nums[0] + nums[1] ,其中 1 < i,j < nums.length,且所有积木不都相等。
此时后续遍历一层长度范围是: nums[0] ~ nums[0] + nums[1]时,会产生冗余判断。
更优的策略是,将一层长度最大值定义为 nums[0] + nums[-1],即单个积木最大长度 + 单个积木最小长度,此时才能保证 nums[i] + nums[j] 不是必然小于 nums[0] + nums[1]的。
比如积木长度降序列表为:5 4 3 3 2 1
如果一层两个积木取5+4=9,则必然没有任意其他两个积木和=9的
但是如果一层两个积木取5+1=6,则有4+2,3+3可以组成相同长度的一层
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const nums = line.split(" ").map(Number);
console.log(getResult(nums));
});
function getResult(nums) {
const n = nums.length;
// 如果只有一个积木,那么只能是一层高度
if (n == 1) return 1;
// 如果有两个积木
// 如果两个积木长度相同,则最大高度为2
// 如果两个积木长度不同,则最大高度为1
if (n == 2) return nums[0] != nums[1] ? 1 : 2;
// 积木按长度降序
nums.sort((a, b) => b - a);
// 一层的最小长度,即最长的积木的长度
const minLen = nums[0];
// 一层的最大长度
const maxLen = nums[0] + nums.at(-1);
// 尝试minLen和maxLen中每一个值作为一层长度
for (let len = minLen; len <= maxLen; len++) {
// 对应一层长度限制下的最大高度
let height = 0;
// 通过l,r指针去选择组成一层的一个或两个积木
// l指针指向最大长度的积木
let l = 0;
// r指针指向最小长度的积木
let r = n - 1;
// 如果最大长度的积木,可以独立一层,则l++,height++
while (l < n && nums[l] == len) {
l++;
height++;
}
// 如果 l,r积木无法组成一层
// 假设nums[l] + nums[r] > length,则必然nums[l] + nums[r-1] > length,
// 因为nums已降序,nums[r-1] >= nums[r],即必然l积木无法和其他积木组成一层
// 假设nums[l] + nums[r] < length,则必然nums[l+1] + nums[r] < length,
// 因为nums已降序,nums[l+1] <= nums[l],即必然r积木无法和其他积木组成一层
while (l < r) {
if (nums[l] + nums[r] != len) break;
l++;
r--;
height++;
}
// 如果正常结束,则必然l > r,否则就是异常结束
if (l <= r) continue;
return height;
}
return -1;
}
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Integer[] nums =
Arrays.stream(sc.nextLine().split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
System.out.println(getResult(nums));
}
public static int getResult(Integer[] nums) {
int n = nums.length;
// 如果只有一个积木,那么只能是一层高度
if (n == 1) {
return 1;
}
// 如果有两个积木
if (n == 2) {
// 如果两个积木长度相同,则最大高度为2
// 如果两个积木长度不同,则最大高度为1
return nums[0] - nums[1] != 0 ? 1 : 2;
}
// 积木按长度降序
Arrays.sort(nums, (a, b) -> b - a);
// 一层的最小长度,即最长的积木的长度
int minLen = nums[0];
// 一层的最大长度
int maxLen = nums[0] + nums[nums.length-1];
// 尝试minLen和maxLen中每一个值作为一层长度
for (int len = minLen; len <= maxLen; len++) {
// 对应一层长度限制下的最大高度
int height = 0;
// 通过l,r指针去选择组成一层的一个或两个积木
// l指针指向最大长度的积木
int l = 0;
// r指针指向最小长度的积木
int r = n - 1;
// 如果最大长度的积木,可以独立一层,则l++,height++
while (l < n && nums[l] == len) {
l++;
height++;
}
// 如果 l,r积木无法组成一层
// 假设nums[l] + nums[r] > length,则必然nums[l] + nums[r-1] > length,
// 因为nums已降序,nums[r-1] >= nums[r],即必然l积木无法和其他积木组成一层
// 假设nums[l] + nums[r] < length,则必然nums[l+1] + nums[r] < length,
// 因为nums已降序,nums[l+1] <= nums[l],即必然r积木无法和其他积木组成一层
while (l < r) {
if (nums[l] + nums[r] != len) break;
l++;
r--;
height++;
}
// 如果正常结束,则必然l > r,否则就是异常结束
if (l <= r) continue;
return height;
}
return -1;
}
}
Python算法源码
# 输入获取
nums = list(map(int, input().split()))
# 算法入口
def getResult():
# 如果只有一个积木,那么只能是一层高度
if len(nums) == 1:
return 1
# 如果有两个积木
if len(nums) == 2:
# 如果两个积木长度相同,则最大高度为2
# 如果两个积木长度不同,则最大高度为1
return 1 if nums[0] != nums[1] else 2
# 积木按长度降序
nums.sort(reverse=True)
# 一层的最小长度,即最长的积木的长度
minLen = nums[0]
# 一层的最大长度
maxLen = nums[0] + nums[-1]
# 尝试minLen和maxLen中每一个值作为一层长度
for length in range(minLen, maxLen + 1):
# 对应一层长度限制下的最大高度
height = 0
# 通过l,r指针去选择组成一层的一个或两个积木
# l指针指向最大长度的积木
l = 0
# r指针指向最小长度的积木
r = len(nums) - 1
# 如果最大长度的积木,可以独立一层,则l++,height++
while l < len(nums) and nums[l] == length:
l += 1
height += 1
while l < r:
# 如果 l,r积木无法组成一层
# 假设nums[l] + nums[r] > length,则必然nums[l] + nums[r-1] > length,因为nums已降序,nums[r-1] >= nums[r],即必然l积木无法和其他积木组成一层
# 假设nums[l] + nums[r] < length,则必然nums[l+1] + nums[r] < length,因为nums已降序,nums[l+1] <= nums[l],即必然r积木无法和其他积木组成一层
if nums[l] + nums[r] != length:
break
else:
l += 1
r -= 1
height += 1
# 如果正常结束,则必然l > r,否则就是异常结束
if l <= r:
continue
return height
return -1
# 算法调用
print(getResult())C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 5000
int getResult();
int cmp(const void *a, const void *b);
int nums[MAX_SIZE];
int nums_size = 0;
int main() {
while (scanf("%d", &nums[nums_size++])) {
if (getchar() != ' ') break;
}
printf("%dn", getResult());
return 0;
}
int getResult() {
// 如果只有一个积木,那么只能是一层高度
if (nums_size == 1) {
return 1;
}
// 如果有两个积木
if (nums_size == 2) {
// 如果两个积木长度相同,则最大高度为2
// 如果两个积木长度不同,则最大高度为1
return nums[0] != nums[1] ? 1 : 2;
}
// 积木按长度降序
qsort(nums, nums_size, sizeof(int), cmp);
// 一层的最小长度,即最长的积木的长度
int minLen = nums[0];
// 一层的最大长度,即最长的两个积木的长度之和
int maxLen = nums[0] + nums[nums_size - 1];
// 尝试minLen和maxLen中每一个值作为一层长度
for (int len = minLen; len <= maxLen; len++) {
// 对应一层长度限制下的最大高度
int height = 0;
// 通过l,r指针去选择组成一层的一个或两个积木
// l指针指向最大长度的积木
int l = 0;
// r指针指向最小长度的积木
int r = nums_size - 1;
// 如果最大长度的积木,可以独立一层,则l++,height++
while (l < nums_size && nums[l] == len) {
l++;
height++;
}
while (l < r) {
// 如果 l,r积木无法组成一层
// 假设nums[l] + nums[r] > length,则必然nums[l] + nums[r-1] > length,因为nums已降序,nums[r-1] >= nums[r],即必然l积木无法和其他积木组成一层
// 假设nums[l] + nums[r] < length,则必然nums[l+1] + nums[r] < length,因为nums已降序,nums[l+1] <= nums[l],即必然r积木无法和其他积木组成一层
if (nums[l] + nums[r] != len) break;
l++;
r--;
height++;
}
// 如果正常结束,则必然l > r,否则就是异常结束
if (l <= r) continue;
return height;
}
return -1;
}
int cmp(const void *a, const void *b) {
return (*(int *) b) - (*(int *) a);
}免责声明:
评论0