题目描述
评估一个网络的信号质量，其中一个做法是将网络划分为栅格，然后对每个栅格的信号质量计算。
路测的时候，希望选择一条信号最好的路线（彼此相连的栅格集合）进行演示。
现给出 R 行 C 列的整数数组 Cov，每个单元格的数值 S 即为该栅格的信号质量（已归一化，无单位，值越大信号越好）。
要求从 [0, 0] 到 [R-1, C-1]设计一条最优路测路线。返回该路线得分。
规则：
- 路测路线可以上下左右四个方向，不能对角
- 路线的评分是以路线上信号最差的栅格为准的，例如路径 8→4→5→9 的值为4，该线路评分为4。线路最优表示该条线路的评分最高。
输入描述
第一行表示栅格的行数 R
第二行表示栅格的列数 C
第三行开始，每一行表示栅格地图一行的信号值，如5 4 5
输出描述
最优路线的得分
备注
- 1 ≤ R，C ≤ 20
- 0 ≤ S ≤ 65535
用例
| 输入 | 3 3 5 4 5 1 2 6 7 4 6 |
| 输出 | 4 |
| 说明 | 路线为：5→4→5→6→6 |
| 输入 | 6 5 3 4 6 3 4 0 2 1 1 7 8 8 3 2 7 3 2 4 9 8 4 1 2 0 0 4 6 5 4 3 |
| 输出 | 3 |
| 说明 | 路线为：3→4→6→3→4→7→7→8→9→4→3→8→8→3→4→4→6→5→4→3 |
题目解析
用例1图示 用例2图示
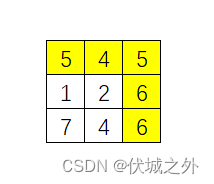
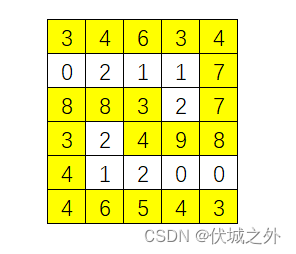
本题需要我们求解 起点(0,0) 到 终点(r-1, c-1) 的所有路径中 "最大的" 最小权值节点的权值。
注：每条路径都由至少一个点组成，而每个点都有权值，因此每条路径自身都有一个最小权值节点。比如路径：5→4→5→6→6，其中最小权值节点的权值就是4
本题需要我们找到起点->终点的所有路径各自的最小权值节点，并比较出其中最大的那个。
其实这个问题就是单源最短路径的变形题，可以使用Dijkstra算法求解，如果不了解Dijistra算法，可以先看下：
下面使用Dijistra算法模拟下用例1的解题过程：
首先，我们需要定义一个dist数组：
- dist[x][y]表示起点(0,0)到终点(x,y)的所有路径中“最大的”最小权值节点的权值
由于dist[x][y]最终记录的是一个最大值，因此我们需要将dist[x][y]初始化为一个最小值，方便后面被更大值替换，由于本题节点（栅格）的权值（信号强度）最小为0，因此这里dist[x][y]可以初始化为0。
初始时，我们将dist数组所有元素都初始化为0，其中dist[0][0] = matrix[0][0]，因为起点(0,0)到终点(0,0)的路径中只有一个节点(0,0)。
之后，我们需要定义一个优先队列pq，pq记录路径的终点（x,y），各路径终点的优先级为：对应路径"最大的"最小权值节点的权值，即dist[x][y]，即dist[x][y]越大，则对应路径终点(x,y)在优先队列中的优先级越高。
初始时，将(0,0)加入优先队列。
下面开始从优先队列不停取出优先级最高的节点：
每当从优先队列中取出一个路径终点（优先级最高），则可以获得如下信息：
- 路径终点的位置 (ux, uy)
- 路径的最小权值节点的权值：dist[ux][uy]
之后基于(ux, uy) 向上下左右四个方向探索，如果新位置(vx, vy)不越界，则进入新位置：
- 此时路径终点从(ux, uy)变更为(vx, vy)
- 此时路径的最小权值节点的权值w为：min(dist[ux][uy], matrix[vx][vy])
我们得到了一个新的路径，新路径的终点为(vx, vy)，新路径中最小权值节点的权值w为 min(dist[ux][uy], matrix[vx][vy])
另外，如果 w > dist[vx][vy]，则说明我们找到了起点(0,0)到(vx, vy)的更优路径，即找到了更大的最小权值节点，因此需要更新 dist[vx][vy] = w，然后将新路径加入到pq中重新排优先级。
按此逻辑一直进行，直到pq为空时，我们就找完了起点(0,0)到所有节点的路径的"最大的"最小权值节点的权值。
最后返回 dist[r-1][c-1] 记录的 起点(0,0) 到 (r-1, c-1) 的所有路径中的"最大的"最小权值节点的权值即可。
2023.12.04
本题的优化思路，由于本题固定求(0,0)到(r-1,c-1)的解，即dist[r-1][c-1]，因此一旦dist[r-1][c-1]确定了，即可停止Dijkstra算法，即不需要找到(0,0)到其余点的dist解。
因此，当pq弹出的点是(r-1, c-1)时，即可提前结束，因为此时dist[r-1][c-1]已经被求解出来，且是最优解。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const r = parseInt(await readline());
const c = parseInt(await readline());
const matrix = [];
for (let i = 0; i < r; i++) {
matrix.push((await readline()).split(" ").map(Number));
}
// dist[i]记录的 起点0 到 终点i 的所有路径中“最大的”最小权值节点的权值
// 其中 i 是将二维坐标一维化后的值，比如(x,y)坐标一维化后为 x * c + y; (c是列数)
// dist[i] 记录的 “最大的”最小权值节点的权值，因此需要初始化为一个 "最小的" 最小权值节点的权值，方便后面被更大者取代，由于本题节点的最小权值>=0，因此这里可以初始化为0
const dist = new Array(r * c).fill(0);
// 起点0 到 终点0 路径的最小权值节点就是自身，即matrix[0][0]点的权重
dist[0] = matrix[0][0];
// 优先队列记录路径（终点），并且路径中的最小权值节点的权值越大，优先级越高
// 初始时将(0,0)入队
const pq = [0];
// 上下左右的方向偏移量
const offsets = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1],
];
while (pq.length > 0) {
// 取出优先队列中优先级最大的路径（终点）
const u = pq.pop();
// 将一维化坐标u，解析为二维坐标(x,y)
const y = u % c;
const x = (u - y) / c;
// 已找到dist[r-1][c-1]最优解，则可以提前结束
if (x == r - 1 && y == c - 1) break;
// 向上下左右四个方向探索
for (let [offsetX, offsetY] of offsets) {
// 新位置坐标
const newX = x + offsetX;
const newY = y + offsetY;
// 新位置越界则无法访问
if (newX < 0 || newX >= r || newY < 0 || newY >= c) continue;
// 新位置的一维化坐标
const v = newX * c + newY;
// 当前路径（终点u）的最小权值节点的权值为dist[u]
// 要加入当前路径的新位置的点的权值 matrix[newX][newY]
// 那么形成的新路径的最小权值节点的权值即为 w = min(dist[u], matrix[newX][newY])
const w = Math.min(dist[u], matrix[newX][newY]);
// 形成的新路径的终点为 v（即新位置一维化坐标）
// 而dist[v]记录的是起点到点v的所有路径中“最大的”最小权值节点
if (dist[v] < w) {
// 因此如果dist[v] < w的话，则更新dist[v]
dist[v] = w;
// 并将新路径加入优先队列，参与下一轮比较
pq.push(v);
// 优先级排序，由于34行是pq.pop()，尾部优先级最大，因此这里升序
pq.sort((a, b) => dist[a] - dist[b]);
}
}
}
// 返回起点（0，0）到终点(r-1, c-1)的所有路径中"最大的"最小权值节点的权值
console.log(dist[r * c - 1]);
})();
Java算法源码
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int r = sc.nextInt();
int c = sc.nextInt();
int[][] matrix = new int[r][c];
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
matrix[i][j] = sc.nextInt();
}
}
// dist[i]记录的 起点0 到 终点i 的所有路径中“最大的”最小权值节点的权值
// 其中 i 是将二维坐标一维化后的值，比如(x,y)坐标一维化后为 x * c + y; (c是列数)
// dist[i] 记录的 “最大的”最小权值节点的权值，因此需要初始化为一个 "最小的" 最小权值节点的权值，方便后面被更大者取代，由于本题节点的最小权值>=0，因此这里可以初始化为0
int[] dist = new int[r * c];
// 起点0 到 终点0 路径的最小权值节点就是自身，即matrix[0][0]点的权重
dist[0] = matrix[0][0];
// 优先队列记录路径（终点），并且路径中的最小权值节点的权值越大，优先级越高
PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> dist[b] - dist[a]);
// 初始时将(0,0)入队
pq.add(0);
// 上下左右的方向偏移量
int[][] offsets = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
while (pq.size() > 0) {
// 取出优先队列中优先级最大的路径（终点）
int u = pq.poll();
// 将一维化坐标u，解析为二维坐标(x,y)
int x = u / c;
int y = u % c;
// 已找到dist[r-1][c-1]最优解，则可以提前结束
if (x == r - 1 && y == c - 1) break;
// 向上下左右四个方向探索
for (int[] offset : offsets) {
// 新位置坐标
int newX = x + offset[0];
int newY = y + offset[1];
// 新位置越界则无法访问
if (newX < 0 || newX >= r || newY < 0 || newY >= c) continue;
// 新位置的一维化坐标
int v = newX * c + newY;
// 当前路径（终点u）的最小权值节点的权值为dist[u]
// 要加入当前路径的新位置的点的权值 matrix[newX][newY]
// 那么形成的新路径的最小权值节点的权值即为 w = min(dist[u], matrix[newX][newY])
int w = Math.min(dist[u], matrix[newX][newY]);
// 形成的新路径的终点为 v（即新位置一维化坐标）
// 而dist[v]记录的是起点到点v的所有路径中“最大的”最小权值节点
if (dist[v] < w) {
// 因此如果dist[v] < w的话，则更新dist[v]
dist[v] = w;
// 并将新路径加入优先队列，参与下一轮比较
pq.add(v);
}
}
}
// 返回起点（0，0）到终点(r-1, c-1)的所有路径中"最大的"最小权值节点的权值
System.out.println(dist[r * c - 1]);
}
}
Python算法源码
# 输入获取
r = int(input())
c = int(input())
matrix = [list(map(int, input().split())) for _ in range(r)]
# 算法入口
def getResult():
# dist[i]记录的 起点0 到 终点i 的所有路径中“最大的”最小权值节点的权值
# 其中 i 是将二维坐标一维化后的值，比如(x,y)坐标一维化后为 x * c + y; (c是列数)
# dist[i] 记录的 “最大的”最小权值节点的权值，因此需要初始化为一个 "最小的" 最小权值节点的权值，方便后面被更大者取代，由于本题节点的最小权值>=0，因此这里可以初始化为0
dist = [0] * (r * c)
# 起点0 到 终点0 路径的最小权值节点就是自身，即matrix[0][0]点的权重
dist[0] = matrix[0][0]
# 优先队列记录路径（终点），并且路径中的最小权值节点的权值越大，优先级越高
# 初始时将(0,0)入队
pq = [0]
# 上下左右的方向偏移量
offsets = ((-1, 0), (1, 0), (0, -1), (0, 1))
while len(pq) > 0:
# 取出优先队列中优先级最大的路径（终点）
u = pq.pop()
# 将一维化坐标u，解析为二维坐标(x,y)
x = u // c
y = u % c
# 已找到dist[r-1][c-1]最优解，则可以提前结束
if x == r - 1 and y == c - 1:
break
# 向上下左右四个方向探索
for offsetX, offsetY in offsets:
# 新位置坐标
newX = x + offsetX
newY = y + offsetY
# 新位置越界则无法访问
if newX < 0 or newX >= r or newY < 0 or newY >= c:
continue
# 新位置的一维化坐标
v = newX * c + newY
# 当前路径（终点u）的最小权值节点的权值为dist[u]
# 要加入当前路径的新位置的点的权值 matrix[newX][newY]
# 那么形成的新路径的最小权值节点的权值即为 w = min(dist[u], matrix[newX][newY])
w = min(dist[u], matrix[newX][newY])
# 形成的新路径的终点为 v（即新位置一维化坐标）
# 而dist[v]记录的是起点到点v的所有路径中“最大的”最小权值节点
if dist[v] < w:
# 因此如果dist[v] < w的话，则更新dist[v]
dist[v] = w
# 并将新路径加入优先队列，参与下一轮比较
pq.append(v)
# 优先级排序，由于24行是pq.pop()，尾部优先级最大，因此这里升序
pq.sort(key=lambda i: dist[i])
# 返回起点（0，0）到终点(r-1, c-1)的所有路径中"最大的"最小权值节点的权值
return dist[r * c - 1]
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define MAX_SIZE 400
int cmp(const void *a, const void *b) {
return *((int *) b) - *((int *) a);
}
int main() {
int r, c;
scanf("%d %d", &r, &c);
int matrix[r][c];
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
scanf("%d", &matrix[i][j]);
}
}
// dist[i]记录的 起点0 到 终点i 的所有路径中“最大的”最小权值节点的权值
// 其中 i 是将二维坐标一维化后的值，比如(x,y)坐标一维化后为 x * c + y; (c是列数)
// dist[i] 记录的 “最大的”最小权值节点的权值，因此需要初始化为一个 "最小的" 最小权值节点的权值，方便后面被更大者取代，由于本题节点的最小权值>=0，因此这里可以初始化为0
int dist[MAX_SIZE] = {0};
// 起点0 到 终点0 路径的最小权值节点就是自身，即matrix[0][0]点的权重
dist[0] = matrix[0][0];
// 优先队列记录路径（终点），并且路径中的最小权值节点的权值越大，优先级越高
int pq[MAX_SIZE] = {0};
int pq_size = 0;
// 初始时将(0,0)入队
pq[pq_size++] = 0;
// 上下左右的方向偏移量
int offsets[4][2] = {{-1, 0},
{1, 0},
{0, -1},
{0, 1}};
while (pq_size > 0) {
// 取出优先队列中优先级最大的路径（终点）
int u = pq[--pq_size];
// 将一维化坐标u，解析为二维坐标(x,y)
int x = u / c;
int y = u % c;
// 已找到dist[r-1][c-1]最优解，则可以提前结束
if (x == r - 1 && y == c - 1) break;
// 向上下左右四个方向探索
for (int i = 0; i < 4; i++) {
// 新位置坐标
int newX = x + offsets[i][0];
int newY = y + offsets[i][1];
// 新位置越界则无法访问
if (newX < 0 || newX >= r || newY < 0 || newY >= c) continue;
// 新位置的一维化坐标
int v = newX * c + newY;
// 当前路径（终点u）的最小权值节点的权值为dist[u]
// 要加入当前路径的新位置的点的权值 matrix[newX][newY]
// 那么形成的新路径的最小权值节点的权值即为 w = min(dist[u], matrix[newX][newY])
int w = (int) fmin(dist[u], matrix[newX][newY]);
// 形成的新路径的终点为 v（即新位置一维化坐标）
// 而dist[v]记录的是起点到点v的所有路径中“最大的”最小权值节点
if (dist[v] < w) {
// 因此如果dist[v] < w的话，则更新dist[v]
dist[v] = w;
// 并将新路径加入优先队列，参与下一轮比较
pq[pq_size++] = v;
// 优先级排序，由于43行是pq尾删，即尾部优先级最大，因此这里升序
qsort(pq, pq_size, sizeof(int), cmp);
}
}
}
// 返回起点（0，0）到终点(r-1, c-1)的所有路径中"最大的"最小权值节点的权值
printf("%dn", dist[r * c - 1]);
return 0;
}免责声明：
1、IT资源小站为非营利性网站，全站所有资料仅供网友个人学习使用，禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享，本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题，请立即告知本站，本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体，但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员，一律视为同意网站规定，本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0