题目描述
入职后,导师会请你吃饭,你选择了火锅。
火锅里会在不同时间下很多菜。
不同食材要煮不同的时间,才能变得刚好合适。
你希望吃到最多的刚好合适的菜,但你的手速不够快,用m代表手速,每次下手捞菜后至少要过m秒才能再捞(每次只能捞一个)。
那么用最合理的策略,最多能吃到多少刚好合适的菜?
输入描述
第一行两个整数n,m,其中n代表往锅里下的菜的个数,m代表手速。(1 < n, m < 1000)
接下来有n行,每行有两个数x,y代表第x秒下的菜过y秒才能变得刚好合适。(1 < x, y < 1000)
输出描述
输出一个整数代表用最合理的策略,最多能吃到刚好合适的菜的数量。
用例
| 输入 | 2 1 1 2 2 1 |
| 输出 | 1 |
| 说明 | 无 |
题目解析
题目意思是:
你如果在第 i 秒捞了菜,则需要至少等待 m 秒,即最早在第i+m秒才能进行下一次捞菜。
这里有一个关键点就是,在第 i+m 秒,你可选择不捞菜,之后的时间里,你可以选择任意时刻捞菜,当然捞完后,又要重新等待m秒。
另外本题中,下的菜只有在煮到刚好合适时才能吃,早了或晚了就都不能吃了,这样的话,就不需要用优先队列了,只需要按照煮的菜刚好合适吃的时间点进行升序排序即可。
因此,本题的难度就大大降低了。
如下图,红色点表示菜刚好合适吃了,绿色点是捞菜,橙色是捞完菜后等待时间m
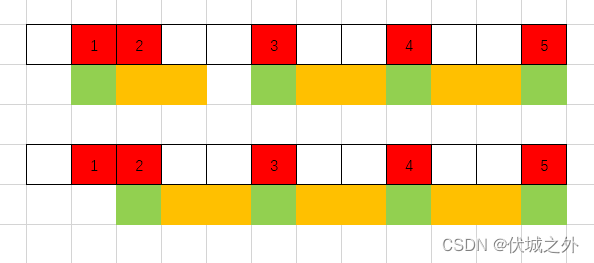
我这里模拟了两种捞菜方案:
- 捞第一个合适吃的菜,即从第1个合适的菜开始捞
- 不捞第一个合适吃的菜,即从第2个合适的菜开始捞
可以发现,两种方案最终捞到的菜数是一样的(每次只能捞一个菜)。
也就是说,你能捞多少菜,并不取决于你从哪个菜开始捞,而是刚好合适的菜之间的间隔时间,由于1和2菜的间隔时间小于m,因此只能二选一,无论你如何规划。
如果两个合适吃的菜的间隔时间大于等于m,则我们两个菜都能吃到,比如3和4,以及4和5。
因此,简单起见,第一个合适吃的菜我们必吃。
假设第k个合适吃的菜出现了,那么我们吃还是不吃呢?
此时要看的并不是第k个合适吃的菜,和第k-1个合适吃的菜的间隔时间,而是看第k个合适吃的菜,和上一次捞菜时间的时间间隔,比如上图中我们是否可以捞第3个菜,看的是其和上一次捞的菜,即第1个菜的时间间隔,而不是而第2个菜的时间间隔。
本题,有点贪心算法的意思,即有合适的菜了,并且捞菜限制没了,就去捞。注意是:先看有没有合适的菜,再看有没有捞菜限制。
但是贪心意味不够明显。
网上还有人说是动态规划,所谓动态规划,即存在状态转移,或者说下一个状态依赖于上一个状态,仔细品品,却是也有点动态规划的味道,因为你能不能捞这个菜,取决于你上次捞菜的时间,这其实也是一种状态转移。
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[] suit = new int[n];
for (int i = 0; i < n; i++) {
suit[i] = sc.nextInt() + sc.nextInt();
}
System.out.println(getResult(n, m, suit));
}
public static int getResult(int n, int m, int[] suit) {
Arrays.sort(suit);
int count = 1; // 第1个合适的菜必吃
int pre = 0;
for (int i = 1; i < suit.length; i++) {
if (suit[i] >= suit[pre] + m) {
// 如果想要捞本次合适的菜,则必须要与上次捞菜的时间差大于等于m,注意这里是suit[pre] + m ,而不是suit[i-1] + m
count++;
// 如果本次捞了菜,则更新缓存本次捞菜的时间点
pre = i;
}
}
return count;
}
}
JS算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let n, m;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
[n, m] = lines[0].split(" ").map(Number);
}
if (n && lines.length === n + 1) {
lines.shift();
const cais = lines.map((line) => line.split(" ").map(Number));
console.log(getMaxSuitCount(cais, m));
}
});
function getMaxSuitCount(cais, m) {
const suit = cais.map((cai) => cai[0] + cai[1]);
suit.sort((a, b) => a - b);
let count = 1; // 第1个合适的菜必吃
let pre = 0;
for (let i = 1; i < suit.length; i++) {
if (suit[i] >= suit[pre] + m) {
// 如果想要捞本次合适的菜,则必须要与上次捞菜的时间差大于等于m,注意这里是suit[pre] + m ,而不是suit[i-1] + m
count++;
pre = i; // 如果本次捞了菜,则更新缓存本次捞菜的时间点
}
}
return count;
}
Python算法源码
# 输入获取
n, m = map(int, input().split())
suit = []
for _ in range(n):
x, y = map(int, input().split())
suit.append(x + y)
# 算法入口
def getResult():
suit.sort()
count = 1 # 第1个合适的菜必吃
pre = 0
for i in range(1, len(suit)):
if suit[i] >= suit[pre] + m:
# 如果想要捞本次合适的菜,则必须要与上次捞菜的时间差大于等于m,注意这里是suit[pre] + m ,而不是suit[i-1] + m
count += 1
# 如果本次捞了菜,则更新缓存本次捞菜的时间点
pre = i
return count
# 调用算法
print(getResult())
免责声明:
评论0