题目描述
n 个学生排成一排,学生编号分别是 1 到 n,n 为 3 的整倍数。
老师随机抽签决定将所有学生分成 m 个 3 人的小组(n == 3 * m) ,
为了便于同组学生交流,老师决定将小组成员安排到一起,也就是同组成员彼此相连,同组任意两个成员之间无其它组的成员。
因此老师决定调整队伍,老师每次可以调整任何一名学生到队伍的任意位置,计为调整了一次, 请计算最少调整多少次可以达到目标。
注意:对于小组之间没有顺序要求,同组学生之间没有顺序要求。
输入描述
第一行输入初始排队顺序序列
第二行输入分组排队顺序序列
输出描述
最少调整多少次数
用例
| 输入 | 4 2 8 5 3 6 1 9 7 6 3 1 2 4 8 7 9 5 |
| 输出 | 1 |
| 说明 |
分组分别为:6,3,1一组,2,4,8一组,7,9,5一组 初始排队顺序中,只要将5移动到1后面,变为: 4 2 8 3 6 1 5 9 7 即可满足分组排队顺序要求。 因此至少需要调整1次站位。 |
| 输入 | 8 9 7 5 6 3 2 1 4 7 8 9 4 2 1 3 5 6 |
| 输出 | 0 |
| 说明 | 无 |
| 输入 | 7 9 8 5 6 4 2 1 3 7 8 9 4 2 1 3 5 6 |
| 输出 | 1 |
| 说明 | 无 |
题目解析
本题有两个难点:
- 如何快速判断两个小朋友是否为一组
- 如何调整站队,才能花费次数最少
关于1,我们可以根据第二行输入做如下处理(以用例1为例):
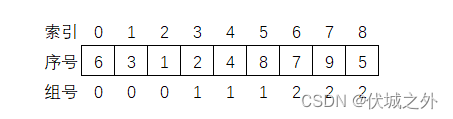
由于第二行输入的分组排队序列,每3个一组,因此我们只要将分组序列的各元素索引值整除3,即可得出各元素(小朋友序号)所在的分组。
即我们可以根据第二行输入,能得到一个:“序号->组号” 的映射关系。
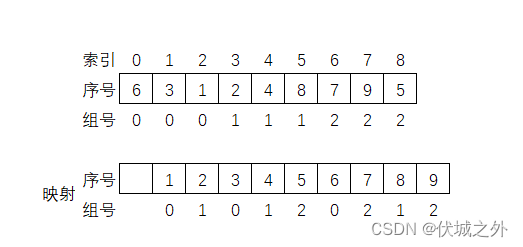
这组映射关系,我们可以保存为一个map数组,map数组索引就是小朋友序号,map数组元素就是小朋友组号。
之后,我们再根据map的映射关系,就可以将第一行输入的初始小朋友(序号)排队顺序,映射为初始小朋友(组号)顺序,比如用例1:
初始小朋友(序号)排队顺序:4 2 8 5 3 6 1 9 7
初始小朋友(组号)排队顺序:1 1 1 2 0 0 0 2 2
之后,分组调整只需要按照 “初始小朋友(组号)排队顺序” 进行即可。
关于2,由于小朋友按3人一组,因此初始组号排队顺序可能存在如下情况:
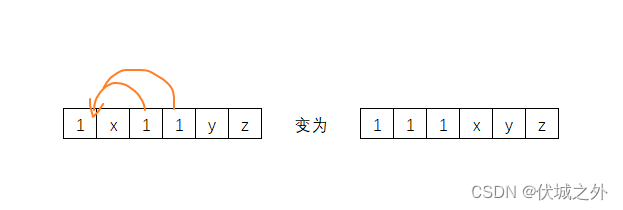
- 1 1 x 1 y z
- 1 x 1 1 y z
- 1 x 1 y 1 z
上面三种情况,我们需要让组号1的小朋友组合在一起。
对于情况1:
我们可以这样调整一次

此时分组1,不会对其他分组造成影响。比如具体示例:
- 1 1 2 1 2 2 按上面策略调整后 1 1 1 2 2 2
- 1 1 2 2 1 2 按上面策略调整后 1 1 1 2 2 2
- 1 1 2 2 2 1 按上面策略调整后 1 1 1 2 2 2
但是,如果我们像下面这样调整,需要调整2次
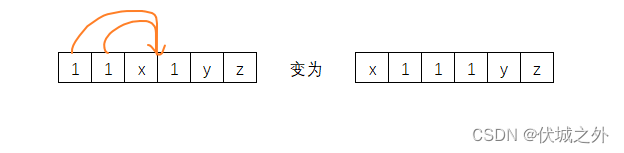
并且可能会影响到x的调整,比如具体示例:
- 1 1 2 1 2 2 按上面策略调整后 2 1 1 1 2 2
- 1 1 2 2 1 2 按上面策略调整后 2 2 1 1 1 2
- 1 1 2 2 2 1 按上面策略调整后 2 2 2 1 1 1
因此,对于情况1而言,最优策略是将后面的单独1并入到开头两个1中,只需要调整1次。
对于情况2:
如果将开头单独1并入后面两个2中,只需要调整一次,但是可能会对x造成影响
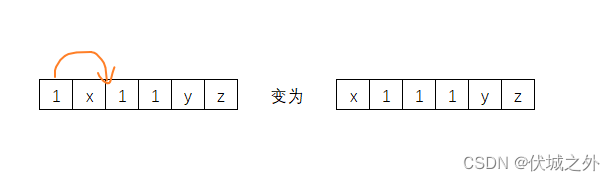
比如:
1 2 2 1 1 2 按照上面策略调整后 2 2 1 1 1 2,此时2还需要至少调整1次
1 2 1 1 2 2 按照上面策略调整后 2 1 1 1 2 2,此时2还需要至少调整1次
但是对于
1 2 2 2 1 1 这种情况,当前调整策略是最优的
如果将后面两个1并入到开头单独1中,那么需要调整2次
比如对于下面情况,当前调整策略是最优的
1 2 2 1 1 2 按照上面策略调整后 1 1 1 2 2 2
1 2 1 1 2 2 按照上面策略调整后 1 1 1 2 2 2
但是对于
1 2 2 2 1 1 这种情况,当前调整策略不是最优。
因此,对于情况2,我们需要判断,开头单独1和后面两个1之间是否是连续完整分组:
- 如果是,那么只需要调整一次,开头单独1并入到后面两个1中
- 如果不是,那么需要调整两次,后面两个1并入到开头单独1中
对于情况3,有如下调整策略:
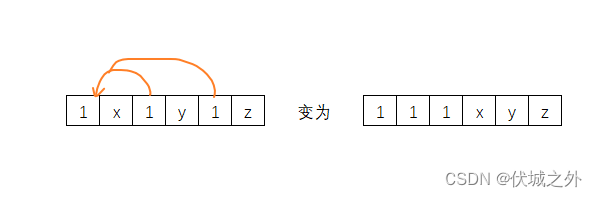
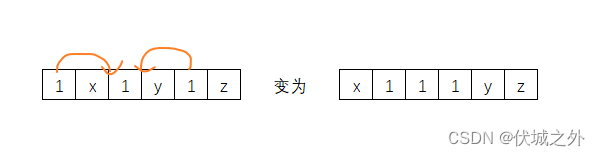

可以发现,无论怎么调整都需要两次。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
// 初始小朋友(序号)排队顺序
let nums = (await readline()).split(" ").map(Number);
const sorted_nums = (await readline()).split(" ").map(Number);
const n = nums.length;
// 序号->组号 映射关系
const map = new Array(n + 1).fill(0);
for (let i = 0; i < n; i++) {
const num = sorted_nums[i];
map[num] = Math.floor(i / 3);
}
// 分块(即连续的相同组的小朋友)
class NumberCount {
constructor(num, count) {
this.num = num;
this.count = count;
}
}
// 按初始排队顺序记录分块
let queue = [];
// 记录组号对应的分块, key是组号,val是对应组号的小朋友分块
const blocks = {};
nums
.map((num) => map[num]) // 序号->组号
.forEach((num) => {
// 相邻相同组号合并为块
if (queue.length == 0 || queue.at(-1).num != num) {
queue.push(new NumberCount(num, 1));
// 记录相同组号的各个分块
if (!blocks[num]) blocks[num] = [];
blocks[num].push(queue.at(-1));
} else {
queue.at(-1).count++;
}
});
// 记录调整次数
let moved_count = 0;
while (queue.length > 0) {
const first = queue.shift();
// 如果开头块是空的,或者开头块已经包含3个小朋友,那么不需要调整位置
if (first.count == 0 || first.count == 3) continue;
if (queue.length == 0) break;
// 第二块
let second = queue[0];
while (second.count == 0) {
queue.shift();
second = queue[0];
}
// 如果开头块和第二块组号相同,则合并(前面并入后面)
if (first.num == second.num) {
second.count += first.count;
continue;
}
/* 如果开头块和第二块组号不同,则进入具体情况分析 */
if (first.count == 2) {
// 开头块有2个小朋友,则情况如下组号1例子,此时需要将后面的单独1,并入开头两个1中,即调整一次
// 1 1 x 1
moved_count += 1;
// 后面单独1所在块的小朋友数量清空
blocks[first.num].forEach((block) => (block.count = 0));
continue;
}
if (first.count == 1) {
// 开头块只有1个小朋友,则有两种情况
if (blocks[first.num].length == 3) {
// 对于组号的分块有三个,即如下组号1例子
// 1 x 1 y 1 z
// 此时需要将后面两个单独1,并入到开头1中,即调整两次
moved_count += 2;
// 后面两个单独1所在块的小朋友数量清空
blocks[first.num].forEach((block) => (block.count = 0));
} else {
// 对于组号的分块有两个,则如下组号1例子
// 1 x 1 1
// 此时需要将开头单独1并入到后面两个1中,即调整一次
moved_count += 1;
// 后面两个1所在块的小朋友数量变为3个
blocks[first.num].forEach((block) => (block.count = 3));
}
}
}
console.log(moved_count);
})();
Java算法源码
import java.util.*;
public class Main {
// 分块(即连续的相同组的小朋友)
static class NumCount {
int num;
int count;
public NumCount(int num, int count) {
this.num = num;
this.count = count;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 初始小朋友(序号)排队顺序
int[] nums = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int n = nums.length;
// 序号->组号 映射关系
int[] map = new int[n + 1];
for (int i = 0; i < n; i++) {
int num = sc.nextInt();
map[num] = i / 3;
}
// 初始小朋友(组号)排队顺序
nums = Arrays.stream(nums).map(num -> map[num]).toArray();
// key是组号,val是对应组号的小朋友分块
HashMap<Integer, ArrayList<NumCount>> blocks = new HashMap<>();
// 相邻相同组号合并为块
LinkedList<NumCount> queue = new LinkedList<>();
for (int num : nums) {
if (queue.isEmpty() || queue.getLast().num != num) {
queue.addLast(new NumCount(num, 1));
// 记录相同组号的各个分块
blocks.putIfAbsent(num, new ArrayList<>());
blocks.get(num).add(queue.getLast());
} else {
queue.getLast().count++;
}
}
// 记录调整位置次数
int moved_count = 0;
while (queue.size() > 0) {
NumCount first = queue.removeFirst();
// 如果开头块是空的,或者开头块已经包含3个小朋友,那么不需要调整位置
if (first.count == 0 || first.count == 3) continue;
if (queue.size() == 0) break;
// 第二块
NumCount second = queue.getFirst();
while (second.count == 0) {
queue.removeFirst();
second = queue.getFirst();
}
// 如果开头块和第二块组号相同,则合并(前面并入后面)
if (first.num == second.num) {
second.count += first.count;
continue;
}
/* 如果开头块和第二块组号不同,则进入具体情况分析 */
if (first.count == 2) {
// 开头块有2个小朋友,则情况如下组号1例子,此时需要将后面的单独1,并入开头两个1中,即调整一次
// 1 1 x 1
moved_count += 1;
// 后面单独1所在块的小朋友数量清空
blocks.get(first.num).forEach(block -> block.count = 0);
continue;
}
if (first.count == 1) {
// 开头块只有1个小朋友,则有两种情况
if (blocks.get(first.num).size() == 3) {
// 对于组号的分块有三个,即如下组号1例子
// 1 x 1 y 1 z
// 此时需要将后面两个单独1,并入到开头1中,即调整两次
moved_count += 2;
// 后面两个单独1所在块的小朋友数量清空
blocks.get(first.num).forEach(block -> block.count = 0);
} else {
// 对于组号的分块有两个,则如下组号1例子
// 1 x 1 1
// 此时需要将开头单独1并入到后面两个1中,即调整一次
moved_count += 1;
// 后面两个1所在块的小朋友数量变为3个
blocks.get(first.num).forEach(block -> block.count = 3);
}
}
}
System.out.println(moved_count);
}
}
Python算法源码
# 分块(即连续的相同组的小朋友)
class NumberCount:
def __init__(self, num, count):
self.num = num
self.count = count
# 输入获取
nums = list(map(int, input().split())) # 初始小朋友(序号)排队顺序
sorted_nums = list(map(int, input().split())) # 小朋友(序号)分组排队顺序
n = len(nums)
# 序号->组号 映射关系
mapping = [0] * (n + 1)
for i in range(n):
num = sorted_nums[i]
mapping[num] = i // 3
# 初始小朋友(组号)排队顺序
nums = map(lambda x: mapping[x], nums)
# 算法入口
def getResult():
# 按初始排队顺序记录分块
queue = []
# 记录组号对应的分块, key是组号,val是对应组号的小朋友分块
blocks = {}
for num in nums:
if len(queue) == 0 or queue[-1].num != num:
# 相邻相同组号合并为块
queue.append(NumberCount(num, 1))
# 记录相同组号的各个分块
blocks.setdefault(num, [])
blocks[num].append(queue[-1])
else:
queue[-1].count += 1
# 记录调整次数
moved_count = 0
while len(queue) > 0:
first = queue.pop(0)
# 如果开头块是空的,或者开头块已经包含3个小朋友,那么不需要调整位置
if first.count == 0 or first.count == 3:
continue
if len(queue) == 0:
break
# 第二块
second = queue[0]
while second.count == 0:
queue.pop(0)
second = queue[0]
# 如果开头块和第二块组号相同,则合并(前面并入后面)
if first.num == second.num:
second.count += first.count
continue
"""
如果开头块和第二块组号不同,则进入具体情况分析
"""
if first.count == 2:
# 开头块有2个小朋友,则情况如下组号1例子,此时需要将后面的单独1,并入开头两个1中,即调整一次
# 1 1 x 1
moved_count += 1
# 后面单独1所在块的小朋友数量清空
for block in blocks[first.num]:
block.count = 0
continue
if first.count == 1:
# 开头块只有1个小朋友,则有两种情况
if len(blocks[first.num]) == 3:
# 对于组号的分块有三个,即如下组号1例子
# 1 x 1 y 1 z
# 此时需要将后面两个单独1,并入到开头1中,即调整两次
moved_count += 2
# 后面两个单独1所在块的小朋友数量清空
for block in blocks[first.num]:
block.count = 0
else:
# 对于组号的分块有两个,则如下组号1例子
# 1 x 1 1
# 此时需要将开头单独1并入到后面两个1中,即调整一次
moved_count += 1
# 后面两个1所在块的小朋友数量变为3个
for block in blocks[first.num]:
block.count = 3
return moved_count
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 90000
typedef struct ListNode {
int num;
int count;
struct ListNode* next;
} ListNode;
typedef struct LinkedList {
int size;
ListNode* head;
ListNode* tail;
} LinkedList;
LinkedList* new_LinkedList() {
LinkedList* link = (LinkedList*) malloc(sizeof(LinkedList));
link->size = 0;
link->head = NULL;
link->tail = NULL;
return link;
}
void addFirst_LinkedList(LinkedList* link, int num, int count) {
ListNode* node = (ListNode*) malloc(sizeof(ListNode));
node->num = num;
node->count = count;
node->next = NULL;
if(link->size == 0) {
link->head = node;
link->tail = node;
} else {
node->next = link->head;
link->head = node;
}
link->size++;
}
void addLast_LinkedList(LinkedList* link, int num, int count) {
ListNode* node = (ListNode*) malloc(sizeof(ListNode));
node->num = num;
node->count = count;
node->next = NULL;
if(link->size == 0) {
link->head = node;
link->tail = node;
} else {
link->tail->next = node;
link->tail = node;
}
link->size++;
}
ListNode* removeFirst_LinkedList(LinkedList* link) {
if(link->size == 0) exit(-1);
ListNode* removed = link->head;
if(link->size == 1) {
link->head = NULL;
link->tail = NULL;
} else {
link->head = link->head->next;
}
link->size--;
return removed;
}
LinkedList* confirm(LinkedList* queue, int confirmed_num) {
// 此方法用于剔除掉队列中已被调整完位置的小朋友,并且抽离后,尝试合并抽离位置前后的小朋友(如果是同一组)
// 时间复杂度有点高这里,可能会超时
LinkedList* back_queue = new_LinkedList();
while (queue->size > 0) {
ListNode* first = removeFirst_LinkedList(queue);
if(first->num == confirmed_num) {
continue;
}
if(back_queue->size == 0 || back_queue->tail->num != first->num) {
addLast_LinkedList(back_queue, first->num, first->count);
} else {
back_queue->tail->count += first->count;
}
}
return back_queue;
}
int main() {
// 初始小朋友(序号)排队顺序
int nums[MAX_SIZE];
int nums_size = 0;
while (scanf("%d", &nums[nums_size++])) {
if (getchar() != ' ') break;
}
// 序号->组号 映射关系
int map[nums_size + 1];
for (int i = 0; i < nums_size; i++) {
int num;
scanf("%d", &num);
map[num] = i / 3;
}
// 相邻相同组号合并统计
LinkedList* queue = new_LinkedList();
for (int i = 0; i < nums_size; i++) {
int num = map[nums[i]];
if(queue->size == 0 || queue->tail->num != num) {
addLast_LinkedList(queue, num, 1);
} else {
queue->tail->count++;
}
}
// 记录调整次数
int moved_count = 0;
while(queue->size > 0) {
ListNode* first = removeFirst_LinkedList(queue);
// 当first.count = 1 时,情况如下
// 1 x 1 1 y z
// 1 x 1 y 1 z
if(first->count == 1) {
ListNode* x = queue->head;
// 判断x是否存在连续完整分组
while (x->count == 3) {
removeFirst_LinkedList(queue);
x = queue->head;
}
if(x->num == first->num && x->count == 2) {
// 情况:1 2 2 2 x[1 1]
// 将开头1,移动进x中
moved_count += 1;
removeFirst_LinkedList(queue);
} else {
// 情况如下:
// 1 x[2 2] 1 1
// 1 x[2] 1 2 1
// 将后面的两个1移动到开头
moved_count += 2;
queue = confirm(queue, first->num);
}
} else if(first->count == 2) {
// 当first.count == 2 时,情况如下:
// 1 1 x 1 y z
moved_count += 1;
queue = confirm(queue, first->num);
}
}
printf("%dn", moved_count);
return 0;
}免责声明:
评论0