题目描述
给定数组[[2,1],[3 2]],每组表示师徒关系,第一个元素是第二个元素的老师,数字代表排名,现在找出比自己强的徒弟。
输入描述
无
输出描述
无
用例
| 输入 | [[2,1],[3,2]] |
| 输出 | [0,1,2] |
| 说明 |
输入: 第一行数据[2,1]表示排名第 2 的员工是排名第 1 员工的导师,后面的数据以此类推。 输出: 第一个元素 0 表示成绩排名第一的导师,没有徒弟考试超过他; |
题目解析
这题也算有点难度的。难在题目给的信息太少了。
比如,师傅和徒弟是绝对一比一吗?题目没说,那我们应该理解为多对多关系。
自己的师傅的师傅能不能是自己的徒弟,比如A是B的徒弟,B是C的徒弟,C又是A的徒弟,题目没说,那我们应该考虑进这种情况。
另外,按照给定用例来看,师傅的徒弟的徒弟,也算是自己的徒弟。比如A是B的师傅,B是C的师傅,则A也算是C的师傅。因此统计比A强的徒弟时,不仅要统计A的直接徒弟,还要统计A的间接徒弟。
考虑上面情况,我构造了一个极端情况的用例:[[1,4],[1,3],[2,4],[2,1],[3,2]]
图示如下
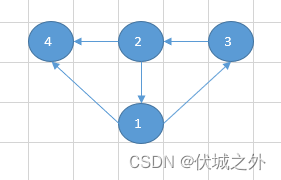
排名1的师傅,有两个直接徒弟排名3和排名4
排名2的师傅,用两个直接徒弟排名1和排名4
排名3的师傅,有一个直接徒弟排名2,两个间接徒弟排1和排名4
排名4的师傅,没有徒弟
因此,输出应该是:
[0, 1, 2, 0]
含义是:
排名1的师傅,没有徒弟排名超过自己,因此返回0
排名2的师傅,有一个排名1的徒弟,因此有一个徒弟排名超过自己,返回1
排名3的师傅,有排名2和排名1的徒弟,因此有两个徒弟排名超过自己,返回2
排名4的师傅,没有徒弟,因此也就没有徒弟排名超过自己,返回0
我的解题思路如下:
首先把每个人的徒弟排名统计出来,比如用例[[1,4],[1,3],[2,4],[2,1],[3,2]] 统计结果为
fa = { '1': [ 4, 3 ], '2': [ 4, 1 ], '3': [ 2 ], '4': [] }
然后我们可以遍历fa对象的每个属性(即师傅排名)和属性值(师傅的直接徒弟的排名)
然后先统计出 “直接徒弟” 中 “排名高于” 师傅的 “徒弟的名次”,比如fa[2]中比2高的名次是1,将统计出来的名词放到一个set集合中保存,接着(递归)继续统计 “间接徒弟” 中 “排名高于” 师傅的 “徒弟的名次”,加入到同一个set中。
直到,统计的徒弟没有徒弟了,或者徒弟是自己(形成环),则终止递归统计。
这样的话,就可以统计出每个师傅下有多少个排名高于自己的徒弟了。
优化动作:
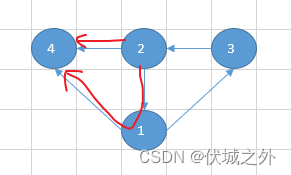
通过上图,我们发现,统计排名2的师傅的“比师傅高排的徒弟”时,排名4的徒弟会被统计两次,一次是作为排名2师傅的直接徒弟,一次是作为排名2师傅的间接徒弟,此时我们应该做剪枝优化。
我们目前会将比师傅排名高的徒弟的排名统计在一个集合highC中,并且通过递归调用getHighC来统计间接徒弟中比祖师排名高的排名,因此,如果调用getHighC之前,发现当前要统计徒弟已经在highC集合中,就无需再次统计,即不调用 getHighC。
补充一个测试用例:
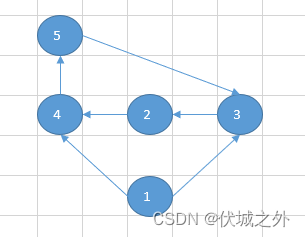
[[1,4],[1,3],[2,4],[3,2],[4,5],[5,3]]
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
rl.on("line", (line) => {
const relations = JSON.parse(line);
console.log(getResult(relations));
});
/**
*
* @param {*} relation 数组,元素也是数组,元素数组含义是[师傅排名,徒弟排名]
*/
function getResult(relations) {
// fa用于统计每个师傅名下的直接徒弟的排名,fa对象的属性是师傅排名,属性值是一个数组,里面元素是直接徒弟的排名
const fa = {};
for (let relation of relations) {
const [f, c] = relation;
fa[f] ? fa[f].push(c) : (fa[f] = [c]);
fa[c] ? null : (fa[c] = []);
}
/**
*
* @param {*} f 当前的师傅,初始时为源头祖师
* @param {*} src 源头祖师
* @param {*} highC 比源头祖师排名的高的徒弟的排名集合
* @returns 比源头祖师排名的高的徒弟的个数,即highC.size
*/
function getHighC(f, src, highC) {
if (f === 1) return 0; // 如果当前师傅是第一名,那么肯定没有徒弟超过它,因此直接返回0
// 遍历当前师傅的所有徒弟
for (let c of fa[f]) {
// flag标记是否需要统计间接徒弟,默认需要
let flag = true;
// 如果徒弟的排名高于源头祖师(排名越高,值越小),则应该统计到highC集合中
if (c < src) {
// 如果highC集合没有这个徒弟,则统计,并需要统计这个徒弟的徒弟(即间接徒弟)的排名情况
if (!highC.has(c)) {
highC.add(c);
}
// 如果highC中已经有了当前的徒弟,则说明当前徒弟已经统计过了,不需要再统计,且当前徒弟的徒弟也不需要再统计了
else {
flag = false;
}
}
// 形成环,需要打断
else if (c === src) {
return 0;
}
if (flag) {
// 统计间接徒弟
getHighC(c, src, highC);
}
}
return highC.size;
}
const ans = [];
// 输出结果要求依次统计:排名第一的师傅的高于自己的徒弟的个数,排名第二的师傅的高于自己的徒弟的个数,......
for (let f in fa) {
ans.push([f, getHighC(f - 0, f - 0, new Set())]);
}
// 按照师傅排名升序后,输出高于师傅排名的徒弟的个数
return ans.sort((a, b) => a[0] - b[0]).map((arr) => arr[1]);
}
Java算法源码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str = sc.nextLine();
// 正则:(?<=]),(?=[) 的含义是,找这样一个“,“,它的前面跟着"]",后面跟着"["
Integer[][] relations =
Arrays.stream(str.substring(1, str.length() - 1).split("(?<=\]),(?=\[)"))
.map(
s ->
Arrays.stream(s.substring(1, s.length() - 1).split(","))
.map(Integer::parseInt)
.toArray(Integer[]::new))
.toArray(Integer[][]::new);
System.out.println(getResult(relations));
}
public static String getResult(Integer[][] relations) {
// fa用于统计每个师傅名下的直接徒弟的排名,fa对象的属性是师傅排名,属性值是一个数组,里面元素是直接徒弟的排名
HashMap<Integer, ArrayList<Integer>> fa = new HashMap<>();
for (Integer[] relation : relations) {
int f = relation[0];
int c = relation[1];
fa.putIfAbsent(f, new ArrayList<>());
fa.putIfAbsent(c, new ArrayList<>());
fa.get(f).add(c);
}
ArrayList<Integer[]> ans = new ArrayList<>();
// 输出结果要求依次统计:排名第一的师傅的高于自己的徒弟的个数,排名第二的师傅的高于自己的徒弟的个数,......
for (Integer f : fa.keySet()) {
ans.add(new Integer[] {f, getHighC(f, f, new HashSet<>(), fa)});
}
// 按照师傅排名升序后,输出高于师傅排名的徒弟的个数
ans.sort((a, b) -> a[0] - b[0]);
return Arrays.toString(ans.stream().map(arr -> arr[1]).toArray(Integer[]::new));
}
/**
* @param f 当前的师傅,初始时为源头祖师
* @param src 源头祖师
* @param highC 比源头祖师排名的高的徒弟的排名集合
* @param fa fa对象的属性是师傅排名,属性值是一个数组,里面元素是直接徒弟的排名
* @return 比源头祖师排名的高的徒弟的个数,即highC.size
*/
public static int getHighC(
int f, int src, HashSet<Integer> highC, HashMap<Integer, ArrayList<Integer>> fa) {
if (f == 1) return 0; // 如果当前师傅是第一名,那么肯定没有徒弟超过它,因此直接返回0
// 遍历当前师傅的所有徒弟
for (int c : fa.get(f)) {
// flag标记是否需要统计间接徒弟,默认需要
boolean flag = true;
// 如果徒弟的排名高于源头祖师(排名越高,值越小),则应该统计到highC集合中
if (c < src) {
if (!highC.contains(c)) {
// 如果highC集合没有这个徒弟,则统计,并需要统计这个徒弟的徒弟(即间接徒弟)的排名情况
highC.add(c);
} else {
// 如果highC中已经有了当前的徒弟,则说明当前徒弟已经统计过了,不需要再统计,且当前徒弟的徒弟也不需要再统计了
flag = false;
}
} else if (c == src) { // 形成环,需要打断
return 0;
}
// 统计间接徒弟
if (flag) getHighC(c, src, highC, fa);
}
return highC.size();
}
}
Python算法源码
# 输入获取
relations = eval(input()) # 二维列表,元素列表含义是[师傅排名,徒弟排名]
def getHighC(fa, f, src, highC):
"""
:param fa: fa用于统计每个师傅名下的直接徒弟的排名,fa对象的属性是师傅排名,属性值是一个数组,里面元素是直接徒弟的排名
:param f: 当前的师傅,初始时为源头祖师
:param src: 源头祖师
:param highC: 比源头祖师排名的高的徒弟的排名集合
:return: 比源头祖师排名的高的徒弟的个数,即highC.size
"""
# 如果当前师傅是第一名,那么肯定没有徒弟超过它,因此直接返回0
if f == 1:
return 0
# 遍历当前师傅的所有徒弟
for c in fa[f]:
# flag标记是否需要统计间接徒弟,默认需要
flag = True
# 如果徒弟的排名高于源头祖师(排名越高,值越小),则应该统计到highC集合中
if c < src:
# 如果highC集合没有这个徒弟,则统计,并需要统计这个徒弟的徒弟(即间接徒弟)的排名情况
if c not in highC:
highC.add(c)
else:
flag = False # 如果highC中已经有了当前的徒弟,则说明当前徒弟已经统计过了,不需要再统计,且当前徒弟的徒弟也不需要再统计了
elif c == src:
return 0 # 形成环,需要打断
if flag:
# 统计间接徒弟
getHighC(fa, c, src, highC)
return len(highC)
# 算法入口
def getResult():
# fa用于统计每个师傅名下的直接徒弟的排名,fa对象的属性是师傅排名,属性值是一个数组,里面元素是直接徒弟的排名
fa = {}
# 输出结果要求依次统计:排名第一的师傅的高于自己的徒弟的个数,排名第二的师傅的高于自己的徒弟的个数,......
for f, c in relations:
if fa.get(f) is not None:
fa[f].append(c)
else:
fa[f] = [c]
if fa.get(c) is None:
fa[c] = []
ans = []
# 输出结果要求依次统计:排名第一的师傅的高于自己的徒弟的个数,排名第二的师傅的高于自己的徒弟的个数,......
for f in fa:
ans.append([f, getHighC(fa, f, f, set())])
# 按照师傅排名升序后,输出高于师傅排名的徒弟的个数
ans.sort(key=lambda x: x[0])
return list(map(lambda x: x[1], ans))
# 算法调用
print(getResult())
免责声明:
评论0